4.6. Понятие о демпфировании электроприводом упругих механических колебаний

Представляя электропривод простейшей структурной схемой на рис. 4.7, необходимо помнить, что неучет упругих механи­ческих связей всегда в той или иной степени искажает факти­ческий характер процессов. Наряду с задачами, для решения которых в конкретных условиях эти искажения не имеют существенного значения, имеется широкий круг практических вопросов, правильно решить которые без учета упругостей невозможно. Кроме того, при решении любых задач нужно уметь оценивать влияние упругих связей на динамику электро­механической системы. Поэтому анализ особенностей взаимо­действия электропривода, обладающего линейной механической характеристикой, с механизмом, содержащим упругие связи, в единой системе имеет важное практическое значение.

Проведем анализ влияния упругих связей с помощью обоб­щенной структуры электромеханической системы, представлен­ной на рис. 4.5. Для удобства анализа процессов по управлению положим Μ_C1=М_С2=0 и воспользуемся преобразо­ванной структурной схемой механической части, приведенной на рис. 1.12,б. Полученная таким образом структурная схема электропривода с упругой связью приведена на рис. 4.14. Здесь передаточные функции механической части выражены через обобщенные параметры γ, Ω₁₂ и Τ_M1=J₁/β,причем γT_Μ1β=J_Σ. (см. § 1.5).

Обращаясь к анализу свойств механической части, выпол­ненному в § 1.5, можно заключить, что в структуре на рис. 4.14 механическая часть объекта представляет собой консервативное колебательное звено, в котором при Μ=const возникшие механические колебания при принятых допущениях не зату­хают. Однако, рассматривая схему на рис. 4.14, можно уста­новить, что колебания скорости двигателя οηблагодаря нали­чию внутренней обратной связи по скорости в системе электро­привода должны вызывать колебания момента, обусловленные динамической жесткостью механической характеристики:

(4.30)

При отсутствии электромагнитной инерции (Т_Э=0)

Сравнивая эту зависимость с (1.18), можно убедиться, что при отсутствии электромагнитной инерции двигатель создает воздействующий на первую массу момент, аналогичный мо­менту вязкого трения. Следовательно, электропривод благодаря наличию электромеханической связи оказывает на колебания в механической части демпфирующее действие, аналогичное действию вязкого трения. Степень затухания колебаний в кон­сервативной механической системе является количественным показателем демпфирующей способности электропривода.

Рассмотрим эффект демпфирования упругих колебаний на простейшем примере, предположив, что момент инерции вто­рой массы настолько велик, что она практически не совершает колебаний (J₂>>J₁),а электромагнитная инерция настолько мала, что можно принять Т_Э=0. Этим условиям соответствуют

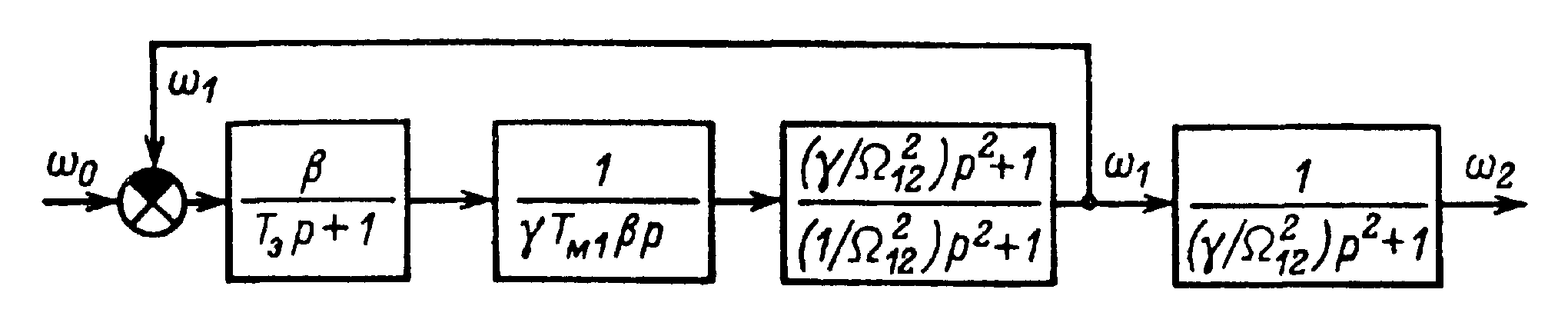
Рис.4.14. Преобразованная структурная схема двухмассовой упругой системы

электромеханическая схема на рис. 4.15, а и структурная схема, изображенная на рис. 4.15, б. Путем преобразования этой структуры получим передаточную функцию объекта по управ­ляющему воздействию ω₀:

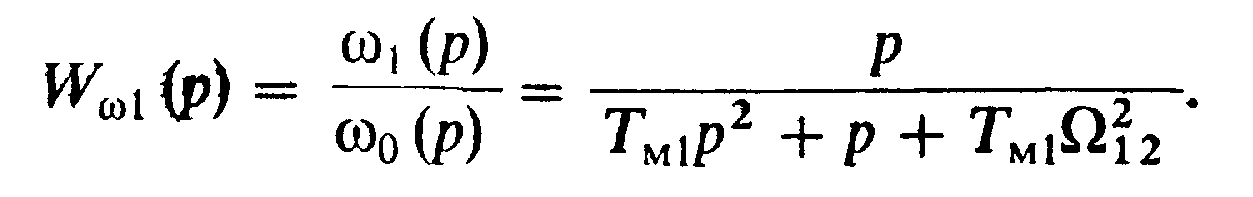(4.31)

Характеристическое уравнение системы

Корни данного уравнения

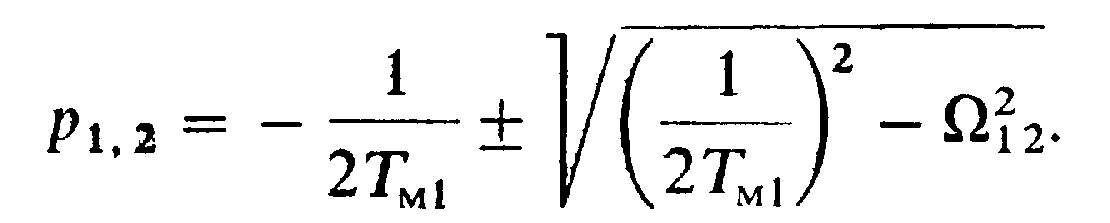
Если Ω₁₂ >½Т_М1корни являются комплексно-сопряженными:

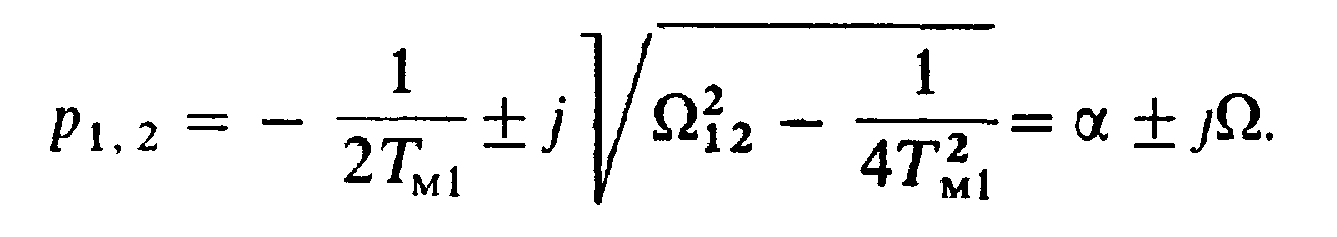(4.32)

Нетрудно видеть, что при Τ_M1≠∞колебания в рассмат­риваемой упругой электромеханической системе затухают вследствие демпфирующего действия электропривода. Рассмот­рим влияние параметров электропривода на затухание коле­баний характеризуемое логарифмическим декрементом

(4.33)

Пусть якорь двигателя питается от источника тока Iя=I₁=const, тогда при Φ=Фном=const Μ=c·I₁=Μ₁=const. Механическая характеристика двигателя, соответствующая это­му режиму, приведена на рис. 4.16,а(прямая1).Ей соот­ветствуют β=0 и Т_М1=∞, при этом по (4.33) λ=0. Следо­вательно, при β=0 демпфирующее действие электропривода на механические колебания отсутствует.

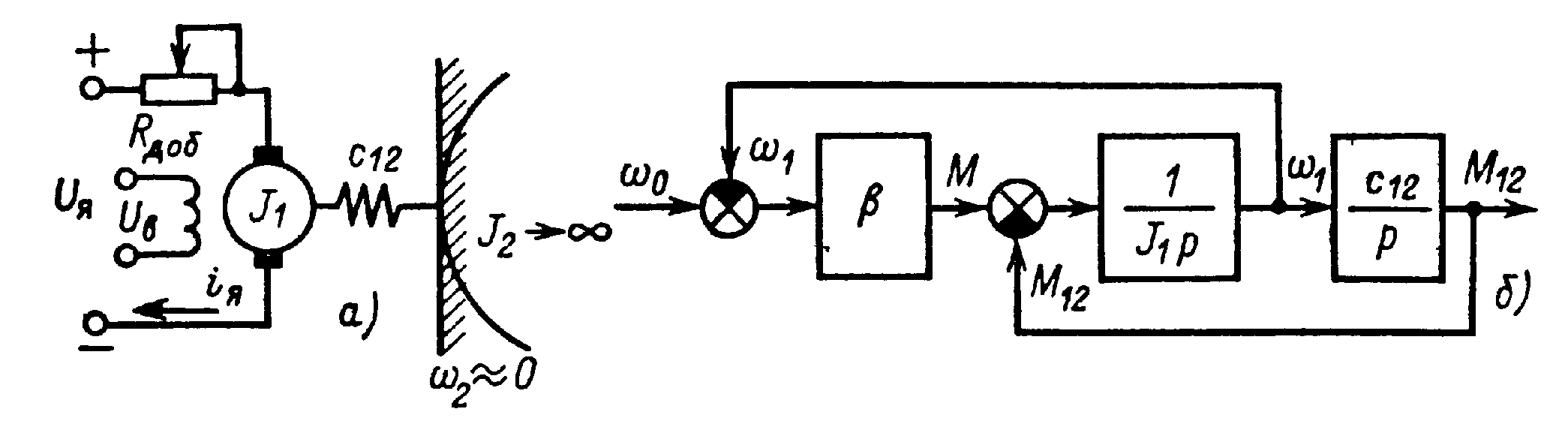
Рис. 4.15. К анализу демпфирующего действия электропривода при J₂=∞и Тэ=0

Подключив якорь к источнику регулируемого напряжения u_я, можно при различных u_я вводить добавочные резисторы R_доб с такими сопротивлениями, при которых I_к,з = I₁ = const, и получить семейство механических характеристик 2–7, показанных на рис. 4.16,a, Этим характеристикам соответствуют значения

=c²/(R_я+R_доб),

изменяющиеся в пределах от 0 до _е. При увеличении  от 0 до _е значения Т_м1, изменяются от  до T_м1е, и в соответствии с (4.33) затухание колебаний постепенно увеличивается. При =_кр, когда 2Т_м1кр₁₂=1, в соответствии с (4.33) = и переходный процесс в системе приобретает апериодический характер. Таким образом, зависимость =() имеет вид, показанный на рис. 4.16,6 (кривая 1). Рассматривая эту кривую, можно убедиться, что изменение жесткости механической характеристики является эффективным средством изменения колебательности системы. Каждому значению J₁ и c₁₂ соответствует определенное значение _кр, обеспечивающее критическое демпфирование (=):

При J₂ дальнейшее увеличение _кр в области >_кр в соответствии с (4.32) вызывает монотонное возрастание коэффициента затухания , так как вторая масса колебаний совершать не может. При конечных значениях J₂ и  вторая масса вовлекается в процесс колебаний, причем в случае жесткой заделки первой массы возникшие колебания не затухают. Следовательно, если принять, что    и Т_м1  0, то в двухмассовой системе демпфирование должно уменьшаться

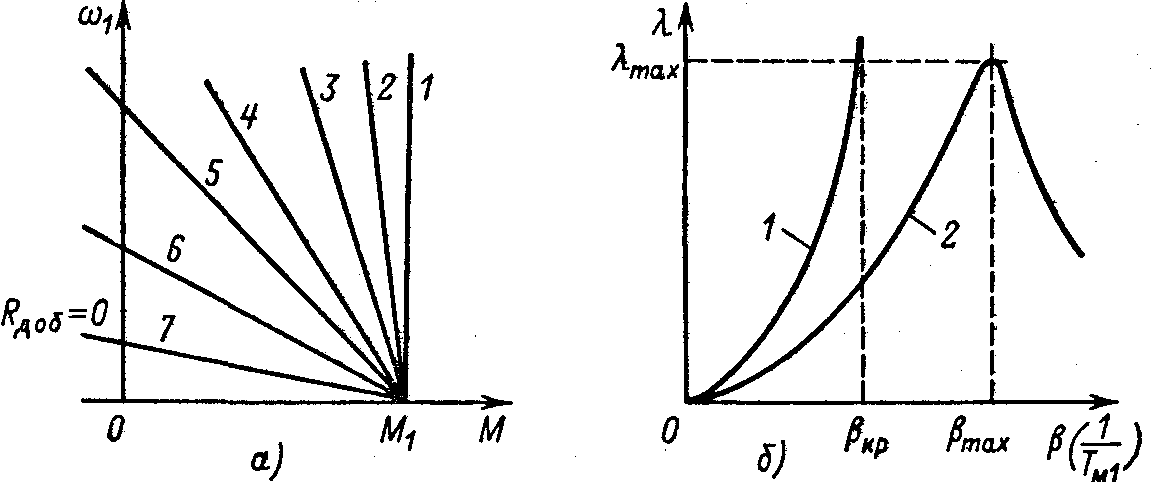
Рис. 4.16. Механические характеристики (а) и соответствующие характеристики демпфирования (б)

При Т_м1* = 0 ( = ) уравнение (4.37) также упрощается:

Корни этого уравнения Переходя к действительному времениt, получаем

(4.38)

где – частота свободных колебаний массыJ₂ при жесткой заделке вала двигателя. В этом случае отсутствуют колебания массы двигателя J₁ и демпфирующая способность электропривода оказывается равной нулю по причине чрезмерно сильной электромеханической связи.

Таким образом, как при предельно слабой электромеханической связи ( = 0), так и при предельно сильной (жесткой) электромеханической связи ( = ) демпфирующий эффект отсутствует и логарифмический декремент (4.36) равен нулю. При увеличении  от нуля Т_м1*= Т_м1₁₂ уменьшается, логарифмический декремент возрастает до максимума и при дальнейшем увеличении    вновь стремится к нулю, как это и показано на рис. 4.16,6 (кривая 2), где значению _max соответствует оптимальное значение (Т_м1*)_max.

Из изложенного следует, что каждому значению  соответствует один максимум _max, который наступает при определенном значении (Т_м1*)_max. Таким образом, _max в системе без электромагнитной инерций зависит только от соотношения инерционных масс =J_/J₁. Оптимальная жесткость механической характеристики зависит от параметров механической части:

_max=J₁₁₂/(Т_м1*)_max (4.39)

Формула (4.39) свидетельствует о том, что чем больше частота свободных механических колебаний системы, тем при большей жесткости _max достигается максимум логарифмического декремента _max.

Современная вычислительная техника позволяет детально исследовать связь демпфирующей способности электропривода с обобщенными параметрами электромеханической системы. Задаваясь различными  и T_э*, можно вычислить соответствующие (4.35) значения , построить семейства зависимостей =(Т_м1*) при =const и T_э*=const, аналогичные кривой 2 на рис. 4.16, б, и далее установить, как изменяются значения _max, в зависимости от T_э* и .

Полученные в результате расчетов на цифровой ЭВМ обобщенные зависимости _max=(Т_э*) и (Т_м1*)_max=(Т_э*) при =const представлены на рис. 4.18. Рассматривая их, можно выявить ряд важных физических особенностей упругой электромеханической системы.

Возможное демпфирование колебании в соответствии с рис. 4.18 тем выше, чем больше , т. е. чем больше приведенный момент инерции механизма. При малых  (см. кривую для =1,5) в широком диапазоне значений Т_э* _max < 2. При этом выбором параметров электромеханического преобразователя невозможно обеспечить высокодемпфированные процессы в упругой системе.

Кривая, соответствующая  = 1,5 свидетельствует о том, что электромагнитная инерция в определенных пределах позволяет увеличить демпфирование (_пред = 2,2) и соответствует значительным Т_э*, в то время как при Т_э* = 0, _max = 0,85, т. е. ниже в 2,6 раза.

Так как индуктивность диссипативными свойствами не обладает, возможность ее демпфирующего действия требует разъяснений. При малых  и m < 4 система имеет две пары комплексных корней и две резонансные частоты, из которых первая пара и первая частота характеризуют колебательность двигателя, а вторая резонансная частота близка к частоте свободных механических колебаний. При увеличении индуктивности рассеяния колебательность двигателя, зависящая от m = Т_м1 / Т_э, увеличивается и меньший резонансный пик АЧХ возрастает. Однако увеличение колебательности двигателя при малом моменте инерции J₂ увеличивает электромеханическую связь и отвод энергии механических колебаний в цепь якоря; второй резонансный пик, обусловленный параметрами механической части, соответственно уменьшается.

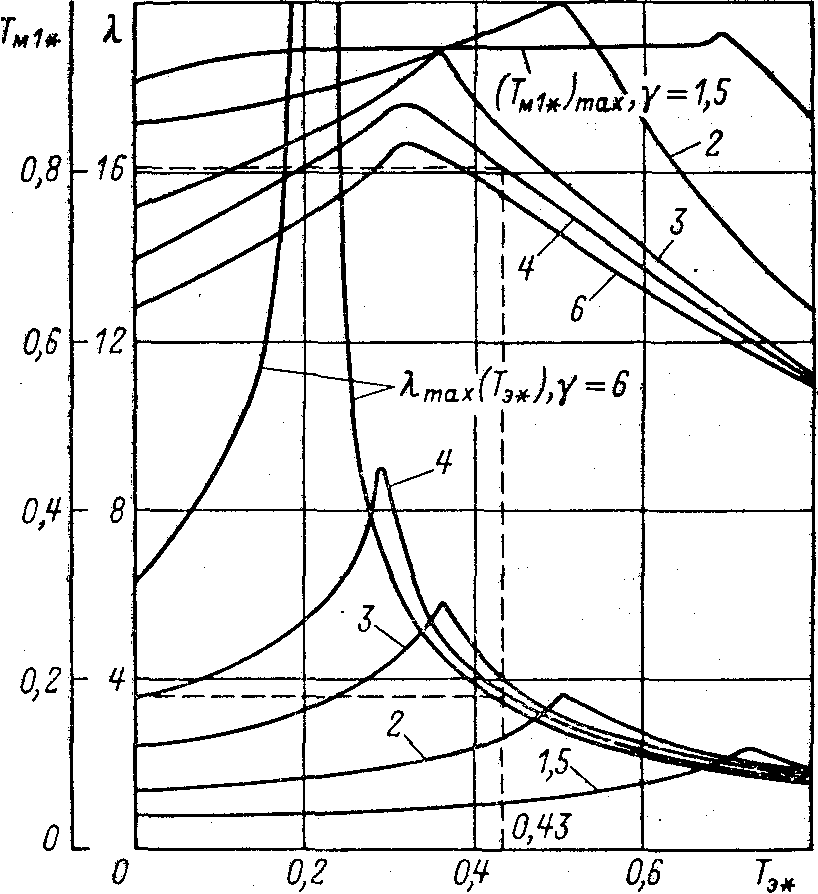
Рис. 4.18. Характеристики максимального демпфирования.

Увеличение индуктивности приводит к уменьшению общей колебательности системы только до того ее значения, при котором наступает равенство резонансных пиков. Дальнейшее увеличение индуктивности вызывает возрастание колебательности. Такие условия наступают тем раньше, чем больше .

При Т_э* = 0 значения _max однозначно определяются соотношением масс . Зависимости _max = () и (T_м*1)_опт = () при Т_э* = 0 представлены на рис. 4.19 (кривые 1 и 1'). Они иллюстрируют закономерность, согласно которой в системе без электромагнитной инерции подбором жесткости механической характеристики получить апериодический характер процессов можно только при   9. При  > 9 критическому демпфированию соответствуют два значения (Т_м1*.)_max и два значения жесткости механической характеристики. Кривая 1' в этой области разветвляется, и заштрихованной зоне соответствуют значения Т_м1*., при которых все корни уравнения (4.37) являются действительными и отрицательными.

Кривые на рис. 4.18 свидетельствуют о том, что варьирование электромагнитной инерционности двигателя позволяет получить при каждом  большее демпфирование, чем при Т_э* = 0. Предельные значения логарифмического декремента, соответствующие каждому , позволяют построить зависимость _пред = () и соответствующие ей зависимости (Т_м1*)_опт = () и (Т_э*)_опт  = () (кривые 2, 2' и 2" на рис. 4.19). Эти кривые показывают, что при наличии электромагнитной инерции Т_э*  0 критическое демпфирование достигается при   5,5, т. е. возможности использования демпфирующего действия электропривода в системах с малым приведенным моментом инерции механизма повышаются.

Представленные на рис. 4.18 характеристики дают возможность определять сочетания параметров, оптимальные по демпфированию колебаний в упругой разомкнутой электромеханической системе.

Пример 4.2. Определить оптимальную по критерию минимума колебательности жесткость механической характеристики электропривода постоянного тока, для которого частные параметры электрической и механической частей имеют следующие значения:

kФ_ном=с=2,84 Вс; R_я=0,098 Ом (в нагретом состоянии машины); Т_я = 0,03 с; J₁ = 3,5 кгкм²; J₂ = 10,5 кгм²; c₁₂ = 548 Нм.

Определим обобщенные параметры, соответствующие (4.35):

 = с²/R_я = 2,84²/0,098 = 82,3 Нмс;

Рис. 4.19. Характеристики предельного демпфирования.

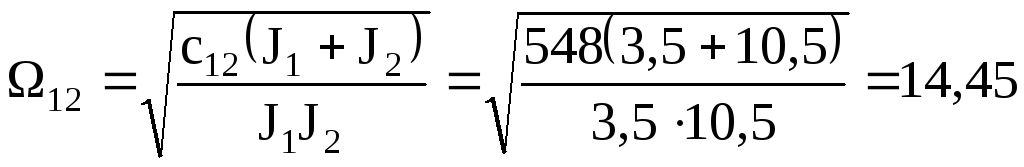1/с

Т_э* = Т_э₁₂ = 0,0314,45 = 0,43; (Т_м1*)_е = J₁₁₂ /  = 3,514,45 / 82,3 = 0,61

При  = 4,0 и Т_э* = 0,43 по кривым рис. 4.18 определяем значения _max и (Т_м1*) _max:

_max = 3,5; (Т_м1*)_max = 0,805

Модуль оптимальной при Т_э* = 0,43 жесткости механической характеристики

_max = J₁₁₂/(Т_м1*)_max3,514,45/0,805 = 63 Нмс,

Сравнивая _max c , можно заключить, что для получения максимального демпфирования при Т_я = 0,03 с жесткость механической характеристики нужно уменьшить на 24%.

Для реализации предельного демпфирования по кривым на рис. 4.18, соответствующим =4,0, необходимо обеспечить значения (Т_э*)_опт = 0,29 и (Т_м1*.)_опт = 0,865.

Следовательно, необходимо уменьшить постоянную времени якорной цепи до значения

Т_я,опт = (Т_э*)_опт / ₁₂ = 0,02 с

Требуемая для предельного демпфирования жесткость механической характеристики составит:

_опт=J₁₁₂/(Т_м1*)_опт=3,514,45/0,865=58,6 Нмс

Следовательно, для реализации предельного демпфирования упругих механических колебаний в данном случае необходимо уменьшить на 33% постоянную времени Т_я и на 28,2% снизить жесткость механической характеристики . Эти изменения в разомкнутой системе могут быть с удовлетворительной точностью обеспечены увеличением сопротивления R_я на 30% путем введения соответствующего добавочного резистора. Полученные значения (Т_э*)_опт и (Т_м1*)_опт могут быть использованы при оптимизации по критерию минимума колебательности электромеханических систем, замкнутых обратными

связями по моменту (току) и скорости.