2. Квантово-механічний опис тунельного ефекту

Звернемося тепер до опису тунельного ефекту в рамках квантової механіки. Опис процесу тунелювання частинок через потенціальний бар'єр міститься в будь-якому курсі квантової механіки. Нижче буде приведено спрощений виклад, лише якісного існування тунельного ефекту. Цей виклад слідує першому розгляду процесу відбиття вільної частки від силового поля, виконаного в 1928 році в рамках квантової механіки Л.І. Мандельштамом і його учнем М.А. Леонтовичем (згодом широко відомим теоретиком) в роботі "До теорії рівняння Шредінгера", опублікованій в головному фізичному журналі тих років "Zeitschrift fur Physique".

Припустимо, що потенціальний бар'єр являєтся стаціонарним, і виходячи з рівняння Шредінгера у формі, не залежній від часу:

(2)

В (2), як і раніше, — повна енергія частинки, — потенціальний бар'єр - оператор Лапласа, а — хвильова функція, що характеризує імовірність знаходження частинки в даній точці.

Вирішуватимемо не реальну тривимірну задачу, а одновимірну. Це дозволяє замінити рівняння (2) в часткових похідних на звичайне дифференціальне рівняння з однією незалежною змінною : (3)

Залежність хвильової функції від часу описується експонентою 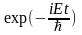, так що можна записувати хвильову функцію у вигляді (4)

Залежна від координати частина хвильової функції задовольняє рівнянню

(5)

Вирішивши рівняння (5) відносно 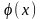, можна одержати з (4) вираз для шуканої хвильової функції 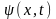. Як бар'єр виберемо просту ступінчасту форму (мал. 1, б):

(6)

Ввівши ці спрощення, перейдемо до обчислення функції для довільного значення аргументу. Звернемося спочатку до області зліва від бар'єра, де . У цій області рівняння (5) зводиться до рівняння

(7)

Легко встановити, що це рівняння має два незалежні розв’язки і , де . Таким чином, в цій області хвильова функція описується виразом

(8) Як видно з (8), розв’язок в цій області представляє собою осцилюючу функцію, що не зростає при .

Звернемося тепер до області праворуч від бар'єру, де . У цій області рівняння (5) зводиться до рівняння

(9)

Легко отримати два незалежні розв’язки цього рівняння, вони мають вигляд

и

де

Другий з цих розв’язків експоненціально зростає із зростанням , що, вочевидь, фізично безглуздо. (Нагадаємо, що початково припускалося, що — хвильова функція, що характеризує вірогідність знахождения частинки.) Таким чином, залишається лише перший з розв’язків рівняння (9) , що відповідає експоненціальному убуванню функції із зростанням величини в області .

Тепер залишається об’єднати розв’язки, отримані для областей з і в точці . Константи А, В і С визначають виходячи з очевидного припущення про безперервність хвильової функції і її першої похідної у всій області зміни величини .

Остаточне вираз для функції має вигляд (10)

(без обмеження спільності можна покласти ).

З виразу (10) видно, що при функція є суперпозицією двох хвиль. Одна з хвиль , поширюється вправо, у бік бар'єру; друга, , — ліворуч від бар'єра. Оскільки модуль множника при у виразі (10) рівний 1, то амплітуди цих хвиль рівні. Таким чином, зліва від бар'єра, при , вираз (8) описує частинку що рухається на бар'єр і таку, що пружно відбивається (мал. 1, б). Цей процес відповідає передбаченням класичної механіки.Проте з виразу (10) також видно, що при хвильова функція проникає за бар'єр в область, заборонену з точки зору класичної механіки. Амплітуда хвильової функції за бар'єром експоненціально зменшується при збільшенні , і при великих вона прямкє до нуля (мал. 1,б)

(11)

Таким чином, праворуч від бар'єру вираз (10) описує тунелювання частинки в класично заборонену область.

З виразу (10) також можна побачити, що при необмежено великій висоті бар'єра ( ) величина прямує до нескінченності. Згідно (10), це означає, що величина при . Таким чином, при безкінечній висоті бар'єра ми повертаємось до класичної картини — частинка за бар'єр не проникає, а лише відбивається від нього. Це підтверджує, що квантова картина при ненескінченно високому бар'єрі можлива.

У тому випадку, коли бар'єр має кінцеву ширину і досить вузький, так що , частинка тунелює за бар'єр з певною вірогідністю і поширюється вправо в просторі за бар'єром (мал. 1, в). При цьому сума вірогідності протунелювати через бар'єр і відбитися від нього рівна одиниці. Відповідно амплітуда хвилі, відбитої від бар'єра, менше амплітуди хвилі, падаючої на бар'єр. Відповідно до формули (11) вірогідність тунелювання експоненціально мала, якщо бар'єр неекстремально вузький.

Конкретна форма бар'єра (який реально ніколи не буває прямокутним) змінює кількісно вірогідність тунелювання, не змінюючи тієї якісної картини, яка отримана вище. Таким чином, завдання, поставлене на початку цього розділу, виконане в рамках квантової механіки: показано існування тунельного ефекту, що приводить до проникнення частинки за бар'єр, висота якого більше енергії частинки.