5. Моделирование систем массового обслуживания

Прежде чем перейти к построению программ имитации случайных процессов протекающих в СМО, рассмотрим на простом примере одноканальной простейшей системы, как осуществляется моделирование.

1. Пошаговое моделирование СМО

Пусть при помощи стандартной функции MathCad runif(n,a,b) получена последовательность из десяти случайных чисел, равномерно распределенных на интервале (0,1).

Используем их для имитации нескольких первых шагов модели. Начальное состояние системы − канал свободен, очереди нет. Входной поток заявок простейший, следовательно, случайный промежуток времени между поступающими заявками распределен по показательному закону

Время обслуживания показательное с параметром μ и

имеет тот же закон распределения Пусть интенсивность потока , а среднее время обслуживания tob=0.2 часа. Так как в момент t=0 система простаивает, то возможным событием может быть лишь приход заявки, занятие ей канала и начало обслуживания − событие А. Первая заявка поступит в систему через часа, или в 0.067 часа.

Теперь возможны следующие случаи − в систему поступит очередная заявка и встанет в очередь (событие А1) или канал освободится и система перейдет в состояние простоя − событие В. Какое из них произойдет, определяется временем прихода требования и временем обслуживания. Так как , то заявка поступит в , а , то конец работы канала в . Таким образом, и произойдет событие А1 − вторая пришедшая заявка встанет в очередь. Далее возможны два события А1 или В1 − заявка покинет канал и требование из очереди попадет в канал. Определим время прихода , и произойдет событие В1. К числу обслуженных заявок нужно прибавить единицу, вычислить время заявки в очереди . Используем четвертое случайное число для определения времени обслуживания , а время прихода , , происходит событие В, число обслуженных заявок , канал освободится и система будет простаивать до . В этот момент заявка займет канал и покинет его в . Очередное требование поступит в (система в это время простаивает), причем обслуживание продлится до 1.23часа, а в 1.2 часа произойдет событие А1 − следующее требование встанет в очередь. В (событие В1) заявка из очереди попадает на обслуживание и покинет канал в 1.54 (по случайному числу ,а пришедшая заявка в1.28 займет место в очереди ( ). Массив случайных чисел исчерпан. Всю последовательность событий и связанных с ними изменениями состоянии системы оформим в виде протокола моделирования.

Протокол моделирования.

Модельное время	Событие	Число обслуженных заявок	Общее время в очереди	Число заявок в очереди	Состояние системы
0.0	-	0	0	0	Простой
0.067	А	0	0	0	Работа
0.223	А1	0	0	1	Работа
0.244	В1	1	0.021	0	Работа
0.374	В	2	0,021	0	Простой
0.440	А	2	0.021	0	Работа
0.99	В	3	0.021	0	Простой
1.157	А	3	0.021	0	Работа
1.2	A1	3	0.021	1	Работа
1.23	В1	4	0.051	0	Работа
1.28	A1	4	0.256	1	Работа

Легко заметить, что время моделирования (машинное время) никак не связано с «реальным» временем, протекающим в системе. Так первая заявка поступит через 0.067 часа после начала процесса, а машинное время на совершение простейшего расчета этой величины имеет порядок долей секунды.

Рассмотрение последовательности событий в приведенном примере дает представление о работе моделирующей программы.

5.2 Моделирование СМО с ограничением на длину очереди.

Для дальнейших сравнений результатов, сначала проведем расчет параметров простейшей СМО. Тогда, - интенсивность входного потока, - среднее время обслуживания и . Число каналов n , каналы нумеруются индексом k . Вероятности состояний в стационарном случае находим для дальнейшего сравнения по обычным формулам [5], так как моделирование позволяет получить только стационарные значения вероятностей.

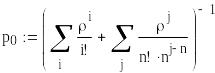
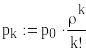
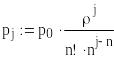
Построение моделирующей программы.

Пусть N – число пришедших заявок, No – число обслуженных, а Np – число потерянных заявок. (В случае неограниченной очереди Np = 0),

Tob – суммарное время затраченное на обслуживание и Toch – суммарное время пребывания заявок в очереди. Для сокращения записи при работе программы и выводе результатов введем матрицу-столбец rem, тогда

В программе и подпрограммах для этой матрицы в качестве формальных параметров используются обозначения re, re1, re2 и т.д. Зададим матрицу для времен постановки заявки в очередь Och (формальный параметр O, O1 …).

Основным алгоритмом моделирования выберем, так называемый, «просмотр активностей». Этот алгоритм заключается в том, что на каждом шаге моделирования просматриваются времена «механизмов» составляющих систему, и выбирается тот, время которого на текущий момент модельного времени наименьшее и который должен произвести действие. В нашем примере моделирования СМО, такими «механизмами» являются: 1) входной поток, 2) каналы обслуживания (по их числу) и 3) очередь. Действиями являются: для входного потока – приход заявки, для канала – начало обслуживания и окончание обслуживания, для очереди – постановка в очередь и уход из очереди в канал. Например, пусть следующая заявка должна поступить в систему в = 12.42, первый канал освободится в 12.56, второй канал свободен, (тогда его время ), третий обслужит заявку в 12.39, а четвертый в 13.05. Минимальное из этих времен 12.39. Следовательно, будет выполнено действие - третий канал освободится, к числу обслуженных заявок прибавится единица, суммарное время обслуживания Tob увеличится на интервал времени, в течение которого заявка была в канале.

(Более подробное описание пошагового моделирования приведено в начале данной главы).

Времена срабатывания «механизмов» записываются в матрицу so (в качестве формальных параметров подпрограмм s, s1 ит.д.).

Для просмотра активностей используется функция,

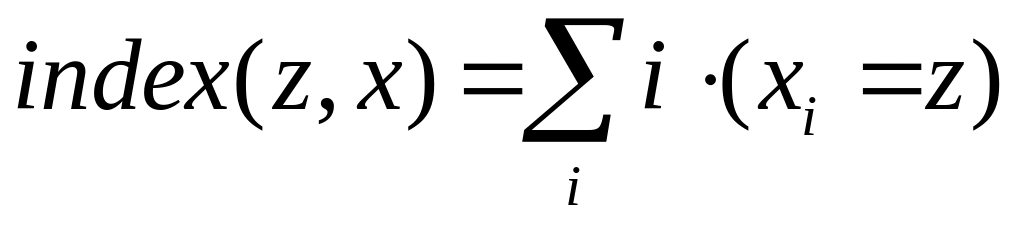
которая определяет номер элемента массива x при выполнении условия , где ”=” логическое равенство. Например, операция

определит минимальный элемент массива s , выделит этот элемент и присвоит переменной ind номер этого элемента. Ниже приведена программа моделирования и ее описание. Заметим, что иногда для большей наглядности и удобства работы с программой ее можно разделить на ряд подпрограмм. Например, выбор канала, в который попадет следующая пришедшая заявка можно осуществить в виде подпрограммы vk

Тогда, при обращении из основной программы к vk(kz,B), эта подпрограмма определит наличие свободных каналов и укажет его номер kz. Здесь В индикатор занятости канала Bk = 0, если k-ый канал свободен Bk = 1 – занят.

Зададим модельное время t = 0 и число занятых мест в очереди m = 0 – очереди нет. Построим цикл while , который будет выполняться пока модельное время, не превысит времени моделирования tm. Обсуждение выбора tm приведено в разделе анализа результатов.

Цикл

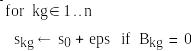
предназначен для исключения возможного зацикливания программы при простое СМО. В этом фрагменте времена срабатывания каналов приводятся к времени прихода следующей заявки плюс некоторая малая положительная величине eps, которая должна быть на 3-4 порядка меньше промежутка между поступающими заявками и не оказывать влияния на процесс моделирования. Этой же цели служит строка

в завершающей части программы.

Блок, связанный с поступлением новой заявки в систему.

Если переменная ind равна нулю, то активным «механизмом» является входной поток и ближайшим действием будет приход заявки. Сначала проверим, превышено ли предельное значение занятых мест в очереди mo.

Если очередь равна или превышает число мест, то фиксируется приход заявки и ее потеря. Если очередь не превысила предельное значение, то запоминаем время прихода предыдущей заявки, увеличиваем число пришедших заявок и определяем время прихода следующей.

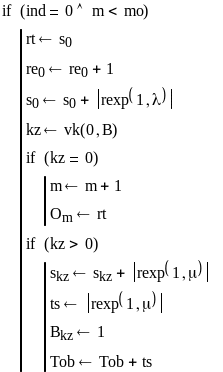
С помощью подпрограммы vk находим свободный канал kz , если их нет, то kz = 0, заявка встает в очередь m = m+1 и запоминается время постановки в очередь Om = rt.

Если свободный канал есть, то находим время обработки заявки ts, назначаем время конца работы этого «механизма», устанавливаем признак занятости этого канала и суммируем время обслуживания Tob = Tob + ts.

Блок, связанный с обслуживанием заявки в канале.

Пусть теперь активен один из каналов обслуживания (ind > 0).

Если, при этом очереди нет, то корректируется время активного канала, к числу обслуженных заявок прибавляется единица и канал с номером ind становится свободным.

.

Если, очередь есть, то к числу обслуженных заявок прибавляется единица, заявка из очереди мгновенно занимает этот канал. Находится время tp пребывания в очереди заявки, которая на данный момент была в очереди первой и вся очередь сдвигается на одно место вперед. Определяется время ts обслуживания пришедшей заявки и корректируется время канала, суммарное время обслуживания и суммарное пребывания в очереди Toch (re4).

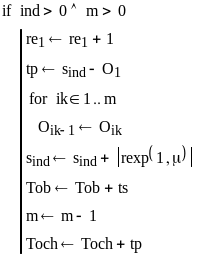
Для определения времени моделирования tmm необходимо провести некоторое число прогонов модели, установить с помощью методов статистики оптимальную длину прогона и количество опытов (пример с вычислением площади круга главы 4). Полный текст программ и расчеты параметров эффективности работы СМО различных типов приведены в Приложении.

Вычисление параметров эффективности системы по результатам прогона модели.

Абсолютную пропускную способность А вычисляем как отношение числа пришедших в систему заявок к времени моделирования. Вероятность отказа находим как число заявок получивших отказ от обслуживания отнесенных к полному числу поступивших требований. Тогда относительная пропускная способность системы (или отношение обслуженных заявок к полному их числу). Существует ряд способов расчета среднего числа заявок в очереди (метод интервалов, метод повторений и т.д.), однако, в виду того, что эти методы достаточно громоздки при расчетах, здесь принят другой подход. Среднее время пребывания требования в очереди легко подсчитать, разделив полное время пребывания в очереди на полное число заявок. А среднее число заявок в очереди можно найти используя формулу Литлла, справедливую для всех типов СМО ,

Аналогично можно поступить и для среднего времени в системе и среднего числа заявок в системе .

5.3 Моделирование СМО с отказами.

Построение программы для этого случая незначительно отличается от описанного выше. Так как очереди нет, то заявка, пришедшая в момент, когда все каналы заняты, покидает систему не получив обслуживания. Соответствующий оператор имеет вид,

.

(Операторы типа не выполняют никаких функций и включены в программу только для сохранения ее структуры).

4. Моделирование простейшей СМО с неограниченной очередью.

Системы с неограниченной очередью, не работают, если коэффициент загрузки , что с формальной точки зрения вызвано расходимостью ряда при вычислении вероятности p0, а фактически соответствует неограниченному возрастанию длины очереди. Отметим, что данный вывод справедлив только для систем, с простейшими потоками, при других законах распределения, например, времени обслуживания, СМО может иметь финальные вероятности состояний и стационарный режим работы и при .

Для исключения ситуаций с неограниченным возрастанием числа заявок в очереди в моделирующей программе имеется блок

.

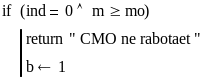Команда “return” прекращает выполнение программы и показывает причину сбоя. Выбор предельного значения mo, при достижении которого моделирование прекращается, формально не обосновывается, но из общих соображений величина 100-200 требований в очереди «достаточна».

5.5 Моделирование СМО с неограниченной очередью при различных законах распределения для входного потока и времени обслуживания.

Пусть случайный промежуток времени между заявками входного потока распределен по произвольному закону f1(t) с математическим ожиданием mot1 и средним квадратичным отклонением sk1. Случайное время обслуживания распределено по закону f2(t) c соответствующими числовыми характеристиками mot2 и sk2. Ограничимся в этой работе тремя законами, а именно, показательным, равномерным и цензурированным нормальным. (Так как промежуток времени не может принимать отрицательные значения, то для нормального распределения нужно либо отбрасывать отрицательные реализации случайной величины, либо брать их по модулю – в этих случаях говорят о цензурированном нормальном законе). Случайные числа для выбранных законов генерируются программами пакета MathCad rexp(n,λ), если распределение показательное, runif(n,a.b) – равномерное, rnorm(n,m,σ) – нормальное. Здесь n – число реализаций, λ, a, b, m, σ параметры распределений.

Для дальнейших сравнений результатов, сначала проведем расчет параметров простейшей СМО.

Тогда, - интенсивность входного потока, - среднее время обслуживания и . Число каналов n , каналы нумеруются индексом k . Вероятности состояний находим по обычным формулам [5]

,

где m, номер занятого места в очереди.

Построение моделирующей программы не отличается от приведенного в предыдущем разделе. Меняются лишь выражения для вычисления случайных времен событий.

Результаты моделирования простейшей СМО, получены при времени моделирования , где − характерное время задачи. При изучении СМО, характерным (определяющим) временем является среднее время между поступающими в систему заявками. Принятая здесь величина tmm в практике моделирования считается приемлемой.

Предварительно проведем расчет параметров эффективности простейшей СМО по точным формулам и определим те же величины при помощи ИМ (здесь все потоки простейшие − времена распределены по показательному закону).

Оценим дисперсию случайной величины - среднего времени в очереди. Для этого проведем 10 прогонов при неизменных параметрах системы и модели.

Результаты удовлетворительны и модель можно считать адекватной.

Переходим к моделированию СМО с другими законами распределения потоков. Пусть входной поток характеризуется равномерным законом, а время обслуживания – нормальное, тогда

Сравнение результатов будем проводить с простейшей системой имеющей те же входные характеристики.

Число обслуженных заявок сократилось на 14%, поэтому параметры СМО, связанные с очередью заметно улучшились. Поменяем использованные выше законы местами.

Результаты моделирования практически не изменились (поэтому здесь не приводятся). В заключение проведем анализ использования детерминированного выходного потока с фиксированным временем обслуживания поступающих заявок tф = mot2. Входной поток простейший.

Абсолютная пропускная способность системы практически не меняется, а параметры очереди заметно лучше.

Таким образом, при законах распределения со временем обслуживания отличном от показательного, параметры эффективности связанные с очередью улучшаются. Это, по-видимому, связано с тем, что вероятность появления очень большого промежутка (более 3σ) обслуживания заявки для показательного закона много больше, чем для нормального и тем более равномерного и детерминированного.

В приложении приведена основная моделирующая программа.

Индивидуальные задания по теме «Системы массового обслуживания».

Задание № 1. Системы массового обслуживания с отказами.

АТС имеет 4 линии связи. Поток вызовов простейший с интенсивностью вызовов в минуту. Время переговоров распределено по показательному закону, среднее время составляет t мин ( ). Информация об исходных данных приведена в таблице.

1. Описать состояния СМО, построить граф состояний.

2. Найти предельные вероятности состояний системы. Найти показатели эффективности работы АТС, проанализировать эти показатели.

3. Изучить зависимость среднего числа занятых каналов и абсолютной пропускной способности АТС от интенсивности входного потока, зависимости представить в виде таблиц и графиков.

4. Определить, сколько линий должна иметь АТС, чтобы вероятность отказа не превышала 0,01.

5. Провести моделирование системы. Сравнить полученные результаты с точными значениями функциональных характеристик.

	№ варианта
	1	2	3	4	5	6	7	8	9	10
	0.9	0.7	0.8	1.3	0.7	0.8	0.9	1.2	1.3	1.1
t	2.9	2.4	0.9	2.6	2.5	2.4	2.5	2.6	2.8	2.3