2. Случайные числа (сч) и методы их получения.

Моделирование систем требует учета стохастических воздействий на систему (случайных событий в случайные моменты времени). Случайные события и случайные промежутки времени можно моделировать с помощью случайных чисел. Методы формирования массивов СЧ можно разделить на физические (аппаратные), табличные и алгоритмические. В машинном статистическом эксперименте, как правило, используют алгоритмический метод. Во всех современных пакетах прикладных программ и языках программирования имеются встроенные функции позволяющие получать массивы СЧ с заданным законом распределения и заданными параметрами. Необходимо иметь в виду, что любая алгоритмическая процедура использует для вычисления СЧ некоторую формулу и, следовательно, получаемая последовательность полностью определена начальными значениями параметров (детерминирована). Такие числа называют псевдослучайными. При дискретном моделировании в качестве базовой выбирают последовательность случайных чисел , равномерно распределенных на интервале (0, 1). Непрерывная случайная величина X имеет равномерное распределение, если ее функция плотности и функция распределения имеют вид

математическое ожидание М(X)=1/2 и дисперсия D(X)=1/12.

Наиболее распространенным методом получения такой последовательности является мультипликативная конгруэнция (в различных модификациях). Два целых числа x и y называются конгруэнтными по модулю m (m –целое число), если |x–y| = km. Таким образом, y конгруэнтно x по модулю m, если |x–y| делиться на m без остатка. Например, при x = 12589 и m = 10, y = 9 конгруэнтно x по модулю 10, а при x = 1223 и m = 2, y = 1 конгруэнтно x по модулю 2. Метод состоит в получении последовательности по рекуррентной формуле

, k = 0,1,2,…

где входные параметры. Такой алгоритм приводит к повторению псевдослучайных чисел начиная с некоторого k. Можно доказать [1], что при

a = 100003, и – девятизначном целом нечетном числе не делящимся на 5, получится не повторяющихся случайных чисел. Очевидно, что при решении задачи необходимо, чтобы полученной последовательности было достаточно для прогона модели.

Продемонстрируем получение первых трех псевдослучайных чисел на примере,

пусть

Тогда, последовательно имеем

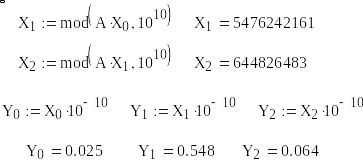и т.д.

Здесь операция mod(Z,V) определяет остаток от деления Z на V.

Число неповторяющихся случайных чисел можно существенно увеличить следующим простым способом. После выбора вычисляются значения и вырезаются числа стоящие, например, в 11,12 и 13 разрядах. Пусть в этих разрядах оказались числа 2, 0, 7 тогда 0,207 следующее случайное число. Этот метод может использоваться и самостоятельно для небольших выборок. После этого находим , описанным выше способом мультипликативной конгруэнции, и получаем последующую серию из чисел. Угол α выбирается произвольно, но меньше 0,5 угловой секунды.

При любом способе получения выборки встает вопрос о качестве этого статистического материала. Тестирование последовательности псевдослучайных чисел должно включать проверки на равномерность, стохастичность и независимость.

Тест на равномерность последовательности проводится по обычной схеме обработки опытных данных. Интервал (0;1) делится на k частей, определяются частоты и по критерию согласия (например, Пирсона) принимаем гипотезу о равномерном законе с некоторым уровнем значимости.

Тест на стохастичность обычно проводят по методу серий. При этом вся исследуемая последовательность делится на элементы первого и второго рода

Серией называется любой отрезок последовательности, состоящий из следующих друг за другом элементов одного рода. Число элементов в этом отрезке называется длиной серии. После таких действий получим, например

…aaabbbbaabaaabbbbbabab…

Так как случайные числа в этой последовательности предполагаются независимыми и равномерно распределенными на интервале (0, 1), то теоретическая вероятность появления серии длиной j в последовательности длиной L в N опытах определяется формулой Бернулли

.

В случае экспериментальной проверки оцениваются частоты появления серий некоторой определенной длины j и сравниваются теоретические и экспериментальные частоты таких появлений, затем по известным критериям согласия делается вывод о принятии или отклонении гипотезы стохастичности получаемых СЧ. В простейшем случае можно ограничиться единственным значением вероятности p, равным, например, медиане последовательности. При более строгом исследовании проделывают указанную процедуру при различных p и различных длинах серий j.

Проверка независимости элементов последовательности псевдослучайных чисел {xi} проводится на основании вычисления корреляционного момента. Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина. Введем в рассмотрение случайную величину , где τ − величина сдвига последовательности. Корреляционный момент двух случайных величин X и Y с реализациями и определяется по формуле

,

где − вероятность того, что величина (X,Y) примет значение . Если случайные числа независимы, то Фактически, при таком анализе, вычисляют коэффициент корреляции . При любом τ ≠ 0 и достаточно больших N , если эмпирическое значение , то с вероятностью β можно утверждать, что полученная последовательность чисел удовлетворяет гипотезе о корреляционной независимости.

Общим подходом построения последовательностей случайных чисел с произвольными законами распределения является метод обратной функции. Пусть требуется создать выборку СЧ, имеющих закон распределения . Если случайное число, из последовательности, имеющей равномерное распределение на интервале (0,1), то возможное значение непрерывной случайной величины X c заданной функцией распределения , является корнем уравнения

или .

Пример 1. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения

.

Требуется найти формулу для нахождения реализаций , соответствующих данным значениям . Запишем , разрешая это уравнение относительно , получим

.

Пусть случайная величина R приняла значения , тогда, при

, получим числа распределенные по показательному закону с заданным параметром λ .

Пример 2. Непрерывная случайная величина Х распределена по закону равномерной плотности на интервале (a,b), заданному функцией распределения

.

Подставляя функцию в уравнение и разрешая его относительно , получим

.

Пример 3. Известно, что если случайная величина представляет собой суперпозицию достаточно большого числа независимых случайных величин с произвольными законами распределения, то она подчиняется нормальному закону. Поэтому для генерирования, нормально распределенного СЧ используют формулу,

,

где m и σ математическое ожидание, и среднее квадратичное отклонение получаемой случайной величины, − СЧ равномерно распределенные на интервале (0,1). Для практических целей достаточно просуммировать 12 таких чисел (n=12).

Задания для лабораторных работ по теме «Случайные числа».

1. Методом мультипликативной конгруэнции сформировать последовательность из n=100 случайных чисел, равномерно распределенных на интервале (0,1). В качестве взять число 3st5st937, где s − первая, а t − вторая цифра по номеру студента в журнале.

2. Провести проверку гипотезы о равномерном законе для полученной выборки (статистический тест).

3. Рассмотреть методом серий вопрос о стохастичности полученных случайных чисел (длина серии j для студента задается преподавателем).

4. Доказать независимость элементов полученной последовательности.

При выполнении лабораторной работы можно использовать примеры программ приводимых в Приложении.

Замечание. Все другие задания следует выполнять, используя случайные числа, получаемые с помощью внутренних функций MathCad.