4.2 Марковская цепь с непрерывным временем

Рассмотрим систему с k состояниями . Переходы между состояниями происходят мгновенно в случайные моменты времени. Вероятности переходов из любого состояния Si в любое другое Sj являются функциями от времени pij(t). Если случайный процесс, протекающий в системе, обладает свойством отсутствия последействия, то говорят, что задана Марковская цепь с непрерывным временем. Интенсивностью перехода из состояния Si в состояние Sj называется предел ,

где вероятность перехода на интервале времени .

Рассмотрим, для примера, Марковскую цепь с тремя состояниями. Пусть задана матрица интенсивностей переходов Λ и начальное распределение вероятностей состояний

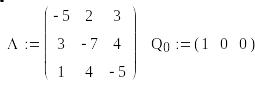
Требуется:

1. Составить размеченный граф состояний этой Марковской цепи, определить, является ли цепь регулярной.

2. Найти стационарное распределение вероятностей состояний.

3. Выполнить моделирование системы и сравнить полученные результаты моделирования с результатами, полученными в пункте 2.

Решение.

1. Составим граф состояний.

2

S1

S2

3

3 1 4 4

S3

По графу видно, что все состояния системы существенны и связаны между собой, поэтому цепь регулярна.

2. По формулам [5] найдем стационарное распределение вероятностей:

,

Тогда стационарное распределение вероятностей состояний Sq [5]

Моделирование процесса, протекающего в данной системе.

Введем переменный массив sj, элементы которого – суммарное время пребывания системы в данном состоянии j, матрицу В – индикатор состояний (каждый столбец соответствует одному состоянию). Например, при выборе столбца 3 система находится в состоянии 2. Напомним, что в этой главе элементы массивов нумеруются так 0,1,2,3…

Моделирующая программа.

Рассмотрим операторы программы по порядку. Задается начальное значение модельного времени t. Вводится матрица iw соответствующая начальному состоянию системы по индикатору состояний и строится цикл while до достижения времени моделирования tm. Определяется номер состояния k, в котором система находится в текущий момент времени. В цикле вычисляем все времена , через которые система может перейти в другое состояние. Находим минимальное из этих времен . Так как цепь Марковская, то

она удовлетворяет условию отсутствия последействия, и случайные времена между переходами распределены по показательному закону. Они могут быть найдены с помощью оператора . Здесь 1 показывает, что вычисляется одно значение, а − интенсивность соответствующего перехода. Полученное время суммируется с временем, которое система провела в текущем состоянии s. Определяется номер ind состояния, в которое переходит система, и этот номер присваивается индикатору В. Отношения времени пребывания в каждом состоянии к полному времени моделирования, принимаются за оценки стационарных вероятностей состояний. Для рассмотренного примера и времени моделирования получим

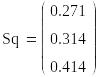
Сравнивая результаты моделирования при различных прогонах с различными числами шагов и точные значения стационарных вероятностей состояний, делаем вывод о хорошей сходимости результатов.

Индивидуальные задания по данному разделу.

Вариант задания следует взять в работе [5] по номеру студента в журнале.

Построить граф состояний Марковской цепи. Показать, что цепь регулярна и имеет финальные вероятности. Решить систему уравнений для вероятностей состояний в стационарном случае. Составить моделирующую программу и провести расчет для своего варианта. Сравнить результаты расчетов по теоретическим формулам и по методу ИМ. В качестве основы для программирования можно использовать разработку программы, приведенную в этом параграфе.