§15 Условное математическое ожидание линии регрессии.
Р
ассмотрим
векторную величину Х(ξ,η).
Условное мат. ожидание
Мат. Ожидание, посчитанное при условии, что одна координата зафиксирована
зафиксирована η.
l – линия регрессии, состоящая из условных мат. ожиданий (регрессия y по х).
l:
- условное мат ожидание.
Вид зависимости между двумя случайными величинами определяется формой линии регрессии.
Пример:
Л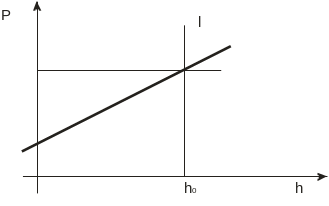
иния
регрессии – ориентировочный средний
вес в данном примере.
§16 Числовые характеристики двумерных случайных величин Корреляционный момент
Двумерная случайная величина X(ξ,
η),
,
Начальным моментом порядка k,l – называется мат ожидание от произведения.
Центральные моменты – это мат ожидание центрированных величин.
Корреляционный момент.
- основная формула корреляционного
момента.
Дисперсия корреляционного момента:
Теорема:
Если две случайные величины независимы между собой, то их корреляционный момент равен 0.
Доказательство:
Дано:
Две независимые случайные величины.
Теорема доказана.
Обратное утверждение неуместно!
Если корреляционный момент двух случайных величин отличен от нуля, то они называются коррелированными.
Корреляционный момент служит для определения являются ли две случайные величины зависимы между собой.
На практике если определили, что k≠0 то случайные величины зависимы, а если k=0 , то либо независимы, либо коррелированны.
Коэффициент корреляции:
- среднеквадратические отклонения.
§17 Виды зависимости между случайными величинами.
Существует 3 основных типа связи между случайными величинами.
Независимые случайные величины.
Стохастическая зависимость. Закон распределения одной случайной величины зависит от того, какие значения принимают другая случайная величина.
Функциональная зависимость между случайными величинами есть функциональная связь, которая выражается формулой.
Функциональная зависимость:
- функциональная зависимость.
Н
а
плоскости все точки не образуют облако.
Точки для лежат на параболе, - на синусоиде.
Для независимых случайных величин облако точек будет в форме прямоугольника.
Стохастическая зависимость:
Есть линия регрессии, которая эту форму определяет.
Точки разбросаны вдоль линии регрессии.
Среди зависимых случайных величин есть коррелированные случайные величины. Геометрически это означает, что линия регрессии близка к прямой линии.
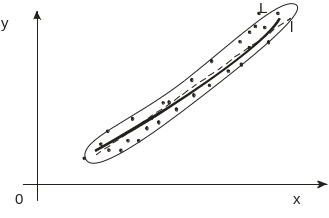
Для нахождения l используют формулу:
l:
- уравнение прямой линии регрессии у по
х.
L=l, L – истинная линия регрессии
Знак перед коэффициентом корреляции
определяет наклон линии. От величины
зависит разброс точек возле линии
регрессии.
Если около 1, то точки практически на прямой.
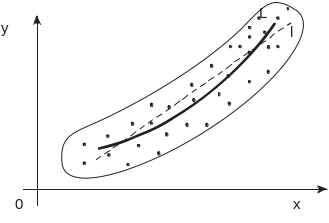
Если
все точки лежат на линии регрессии и
она прямая, зависимость переходит в
функциональную.
Теорема:
Пусть есть двумерная случайная величина X(ξ,η), где ξ,η – имеют нормальный закон распределения, тогда если ξ,η – являются зависимыми , то они являются коррелированными, линия регрессии является прямой.
Коррелированные =зависимые (только для нормального распределения)