§ 3. Этапы составления и исследования моделей.

1. Составление физической модели. Используются принципы идеализации и абстрагирования

Идеализация – это упрощение свойств изучаемых объектов.

Пример:

F=-k·x

Рассматривается идеальная пружина и на всей поверхности действует закон Гука.

Абстрагирование – это отбрасывание некоторых свойств объекта

Пример: пренебрежение трением или давлением воздуха.

2. Составление математической модели - это описание свойств физической модели в математических терминах.

Пример: описание дифференциальными уравнениями.

3. Исследование математической модели математическими средствами.

4. Интерпретация полученных результатов (отношение с физическим и реальным объектом).

5. Определение и оценка точности совпадения полученных результатов в результате моделирования со свойствами реальных объектов.

Пример:

Толкнули груз и он начал колебаться

1. M – материальная точка массы m, действует закон Гука.

F= -k·x, где x – отклонение,

k – жесткость.

Пренебрегаются трение и сопротивление воздуха.

2. Составляются дифференциальные уравнения

Положение груза в момент времени t - x(t)

x’(t) = V

x’(0) = V₀

F(x)= -k·x

З аписывается второй закон Ньютона:

mx”(t) = -k·x;

x(0) = 0;

x’(0) = V₀.

3. Решение уравнений

mx”(t) + k·x=0

mλ² + k·1=0

λ² =-(k/m)

λ_1,2 = ±√(k/m)

x(t)=c₁sin(βt) + c₂cos(βt)

x(0) = 0 = c₁0+ c₂1, => c₂=0

x(t) = c₁sin(βt)

c₁β·1=

- уравнение колебания

3. Получили синусоидальное колебание

,

3. Реального объекта нет, но совпадения будут лучше, если модель будет точнее

§ 4. Имитационное моделирование.

4.1 Статистический эксперимент

З адача: определить значение числа π , бросая камешки.

Бросаем камешки, находясь на расстоянии в квадрат, при этом они равномерно распределены в квадрате.

N – попали в квадрат

k – попали в круг

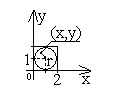
Составим программу, которая покажет, сколько камешков нужно бросить.

N=100

k=10

for n=1:N

x=2·random;

y=2·random;

r=sqrt((x-1)²+ (y-1)²)

if r<=1

k=k+1

end

end

p=4*k/N;

Каждый прогон этой программы для разных N выполняет некий статистический эксперимент. Эта программа есть математическое описание имитационной модели.

4.1 Определение имитационной модели

Имитационная модель – это формальное, т.е. выполненное на формальном языке, описание логики функционирования исследуемой системы и взаимодействие отдельных её элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, обеспечивающие проведение статистического эксперимента.

Отсутствует ограничение по применению и речь может идти только о целесообразности применения. Наибольший эффект применения имитационных моделей, у которых на функционирование оказывают влияние внешние факторы.

Применение имитационного моделирования целесообразно в следующих случаях:

• можно найти аналитическую зависимость выходных параметров системы от количественных характеристик внешних факторов;

• можно находить оптимальные параметры функционирования модели или системы;

• если есть влияние внешних факторов на поведение модели и системы, которое она моделирует.