Пример выполнения задачи 4

Электродвигатель 1 через редуктор 2 приводит в движение из состояния покоя барабан 3 подъемного механизма. Канат 4, укрепленный на барабане и в неподвижной точке О, охватывает подвижный блок 5, к обойме которого на крюке подвешен поднимаемый груз 6 весом Q. В период пуска до достижения номинальной скорости ω_н момент двигателя 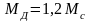, где М_с – момент от веса груза, приведенный к валу двигателя. По достижении ω_н момент двигателя принимает значение 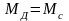и подъем груза осуществляется с постоянной скоростью.

Решая дифференциальное уравнение движения вала двигателя, определить время разгона двигателя до ω_н и время подъема груза на высоту h. Рассчитать и построить диаграммы скорости и перемещения груза в зависимости от времени.

Передаточное отношение редуктора u₁₂, диаметр барабана D, моменты инерции барабана и ротора двигателя J_б и J_р. Массой и толщиной каната пренебречь.

Д ано:

Рис. 5.4, вариант 4
Q, кН	10
D, м	0,2
h, м	20
u12	50
Jб, кг·м2	2
Jп, кг·м2	0,1
ωн, рад/с	100

Решение

Момент на валу барабана

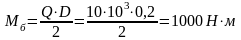
Приведенный момент от груза к валу двигателя

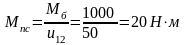
Приведенный момент инерции барабана к валу двигателя

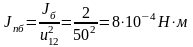
Приведенный момент инерции (суммарный)

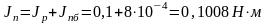
Составим дифференциальное уравнение движения при пуске двигателя

;

;

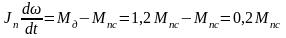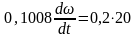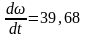
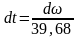
Интегрируем

, где с₁ – постоянная интегрирования, которую определяем с помощью начальных условий:

при t=0 ω=0 – начало движения

,

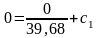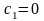
Получили,

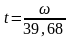
Определим отсюда ω: (*)

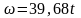Определим время разгона t_р

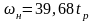
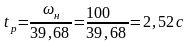– время разгона

при t > t_p, 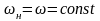– установившиеся движение

т.к. 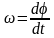, то имеем

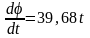
Проинтегрируем

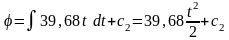, где с₂ – постоянная интегрирования, которую определяем из начальных условий:

при t=0 φ=0

,

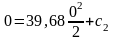Отсюда

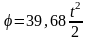– закон движения ротора двигателя при разгоне

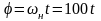– установившиеся движение

При h=20м барабан должен повернуться на угол

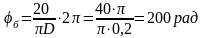
Двигатель должен повернуться на угол

Найдем максимальный угол, на который повернется двигатель при разгоне

Тогда время поднятия груза (t’) при установившимся движении:

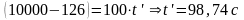
Полное время поднятия груза на высоту h=20м:

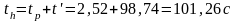– время подъема груза

т.к. 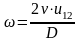, то из уравнения (*), получим

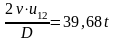
или

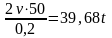
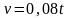– закон изменения скорости груза при разгоне

При t =2,52с – установившаяся скорость

Т.к. 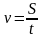, то имеем

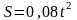или – закон изменения высоты подъема груза

– закон при установившимся движении

Построим диаграммы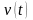 и

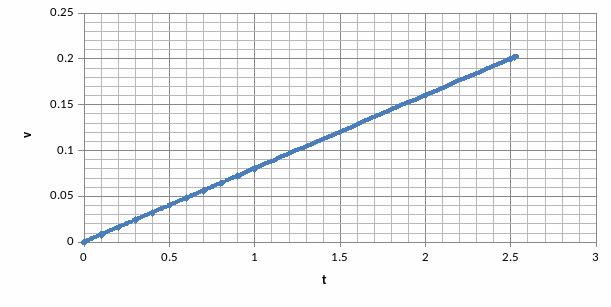
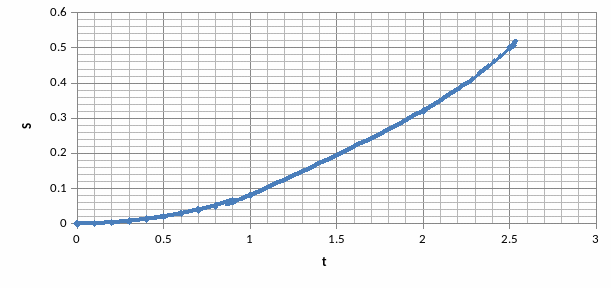
Литература

1. Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1975. – 640 с.

2. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. – М.: Наука, 1973. – 256 с.

3. Под общ. Ред. Девойно Г.Н. Курсовое проектирование по теории механизмов и машин. – Мн.: Выш. шк., 1986. – 286 с.

4. Машков А.А. Теория механизмов и машин. – Мн.: Выш. шк., 1971. – 470 с.

5. Левитский Н.И. Курс теории механизмов и машин. – М.: Наука, 1990. – 592 с.

6. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. – М.: Высш. шк., 1986. – 295 с.: ил.