2 Динамический анализ рычажного механизма

2.1 Постановка задач

При выполнении второго листа КП решаются две задачи:

– определение реакций и уравновешивающей силы методом планов сил, а так же определение уравновешивающей методом Жуковского;

– определение потери и определение мощности двигателя необходимого для привода данного механизма.

К основным задачам динамики относятся следующие:

– определение неизвестных сил действующих на звенья механизма, включая реакции, возникающие в кинематических парах, при этом закон движения входного звена известен;

– определение движения механизма под действием заданных сил приложенных к звеньям механизма.

К первой задаче относят вопросы по уравновешиванию масс в механизме. Ко второй относят исследование колебаний и виброзащиту машин.

Решение обеих задач основывается на принципе Д’Аламбера: звено, диада или механизм в целом можно рассматривать, как находящиеся в равновесии, если к внешним силам, действующим на механизм, условно приложить силы инерции.

Силы, действующие на механизм, классифицируются следующим образом:

– движущие силы – это силы, приложенные к входному звену;

– силы Q полезного сопротивления – силы для преодоления которых создан данный механизм;

– силы вредного сопротивления F: силы сопротивления среды, силы трения;

– веса звеньев G;

– силы инерции Ф – силы обратного воздействия ускоряемого тела на тела, ускоряющие его;

2.2 Построение плана скоростей и ускорений рычажного механизма

На лист 2 графической части курсового проекта (лист 2 ГЧ КП) вычерчиваем схему механизма методом засечек в заданном положении ₁= 150⁰ при выбранном масштабном коэффициенте _S= 0,002 м/мм. К этому положению вычерчиваем план скоростей (не повернутый), учитывая масштабный коэффициент _V= 0,01 ^м/с/мм. Методика построения плана скоростей, а так же методика построения плана механизма и масштабные коэффициенты рассматривались ране в пунктах 1.3 – 1.4.

Рассмотрим несколько основных и необходимых понятий.

Свойство подобия – фигура на плане скоростей (ускорений) звена, образованная векторами относительных скоростей подобно и соответственно расположена с фигурой на звене, образованной теми же точками.

Чтобы определить величину угловой скорости звена следует относительную скорость между точками звена разделить на расстояние между этими двумя точками.

Чтобы определить направление угловой скорости звена, необходимо вектор относительной скорости между двумя точками звена перенести параллельно самому себе в точку звена, не являющуюся полюсом, и повернуть звено вокруг полюса.

Чтобы определить величину углового ускорения звена, необходимо относительное касательное ускорение между двумя точками звена разделить на расстояние между этими точками.

_i = a^_AB/ l_AB, (2.2.1) с.56 [2]

где _i – угловое ускорение звена;

a^_AB – относительное касательное ускорение между двумя точками звена.

Чтобы определить направление _i необходимо относительное касательное ускорение между двумя точками звена перенести параллельно самому себе в точку звена не являющуюся полюсом и повернуть звено в направлении вектора вокруг полюса.

План ускорений строится в той же последовательности, что и план скоростей.

Сначала найдем ускорение точки А конца кривошипа. Точка принадлежит звену 1, совершающему неравномерное вращательное движение, следовательно, ее ускорение будет рассчитываться по следующей формуле:

_ _ _

а_А12= аⁿ_A12 + a^_A12 (2.2.2) c. 73 [5]

где аⁿ_A12 – нормальное ускорение, вектор которого направлен по звену к центру вращения, рассчитывается по формуле (2.2.3)

аⁿ_A12= ₁² * l_OA = 7,54² * 0,09 = 5,11 м/с² (2.2.3) с. 46 [2]

a^_A12 – касательное ускорение, вектор которого направлен перпендикулярно звену и направлен в обратную сторону угловой скорости, т.к. угловое ускорение  получили со знаком «-», рассчитывается по формуле (2.2.4)

a^_A12 = ₁* l_ОА = 1,67 * 0,09 = 0,15 м/с² (2.2.4) с. 46 [2]

О

м/с²

мм

пределяем масштабный коэффициент плана ускорений:

_а = аⁿ_A12/ [n₁] = 5,11/102,2 = 0,05 (2.2.5) c. 46 [2]

Определяем длину отрезка [n₁a₁₂] по формуле (2.2.6):

[n₁a₁₂]= a^_A12/ _а = 0,15/0,05 = 3 мм (2.2.6) с. 46 [2]

На чертеже производим построения. Из произвольного полюса  откладываем в

масштабе вектор аⁿ_A12 параллельно звену ОА. Из конца вектора откладываем ему перпендикулярный отрезок [n₁a₁₂] в направлении обратном угловой скорости входного звена

Конец отрезка соединяем с полюсом и получаем отрезок [a₁₂], характеризующий ускорение звена 1. Используя масштабный коэффициент получаем ускорение а_А12=5,11 м/с².

Ускорение внутренней точки А₃ кулисного камня найдем из системы уравнений:

_ _ _

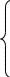a_A3= a_A1,2 + aⁿ_A3A1 + a^k_A3A1 + a^_A3A1

=0 90⁰ //AB

_ _ _ _ (2.2.7) с.46 [2] a_A3= a_В + aⁿ_A3В + a^_A3B

=0 //AВ AB

Кулисный механизм – это звенья, имеющие относительное движение по другим подвижным звеньям. В кулисных механизмах принимаем за относительное движение – движение камня по кулисе, за переносное – движение кулисы.

В формуле (2.2.7) a^k – это ускорение Кориолиса, оно равно удвоенному произведению угловой скорости кулисы ₃ на скорость относительного движения камня по кулисе V_A1A3 (формула 2.2.8):

a^k_A3A1 = 2₃* V _A3A1= 2*1,784* 0,262 = 0,935 м/с² (2.2.8) с. 50 [2]

Определяем отрезок [a₁k] по формуле (2.2.6):

[a₁k] = a^k_A3A1/ _а = 0,935/0.05 = 18,7 мм.

Определяем ускорение aⁿ_A3В по формуле (2.2.9):

aⁿ_A3В = V²_A3B / l_A3B = 0,628²/ 0,35 = 1,13 м/с² (2.2.9) с.50 [2]

Определяем длину отрезка [n₂] по формуле (2.2.6):

[n₂] = aⁿ_A3В / _а = 1,13/ 0,05 = 22,6 мм.

Касательные ускорения a^_A3A1 и a^_A3B находим графическим методом из построений. Из конца вектора ускорения а_А12 откладываем отрезок [a₁k]. Для определения направления кориолисова ускорения (отрезка [a₁k]) необходимо относительную скорость кулисного камня по кулисе повернуть на 90⁰ в сторону вращения кулисы. Из конца отрезка параллельно звену АВ проводим прямую. Далее из полюса  откладываем отрезок [n₂] параллельно звену АВ в направлении к центру вращения звена и из конца отрезка проводим прямую перпендикулярную этому же звену. На пересечении прямых получаем точку а₃. В результате получаем отрезки:

– [а₃к] = 72,9 мм., характеризующий касательное ускорение a^_A3A1

a^_A3A1 = [а₃к] * _а = 72,9 * 0,05 = 3, 65 м/с²

– [а₃n₂] = 17,86 мм., характеризующий касательное ускорение a^_A3B

a^_A3B = [а₃n₂] * _а = 17,86 * 0,05 = 0,89 м/с²

– [а₃] = 28,8 мм., характеризующий ускорение точки а₃

а₃ = [а₃] * _а = 28,8 * 0,05 = 1,44 м/с²

По свойству подобия (аналогично п. 1.4) определяем отрезок [с], а затем, используя масштабный коэффициент, и ускорение точки С – а_с:

[a₃] l_AB

[c ] l_BC (2.2.10) с.57 [4]

откуда

[c ] = l_BC * [a₃] / l_AB = 0,49 * 28,8/ 0,35 = 40,32 мм.,

а_с= [c ] * _а = 40,32 * 0,05 = 2,02 м/с²

Ускорение точки D найдем через систему уравнений по формуле (2.2.11):

_ _ _ _

a _D = a_E + aⁿ_DE + a^_DE

= 0 =0 //DE

_ _ _ _ (2.2.11)с.51[2] а_D= a_C + aⁿ_DC + a^_DC

//DC DC

В системе три величины уже известны. Ускорение точки С из расчетов выше, а ускорение точки Е и нормальное ускорение aⁿ_DE равны нулю. Остается найти три неизвестных. Нормальное ускорение aⁿ_DC рассчитаем по формуле (2.2.9), а

касательные найдем графическим методом.

aⁿ_DC = V²_DC / l_DC = 0,113²/ 0,2 = 0,064 м/с²

Определим длину отрезка [сn₃]:

[сn₃] = aⁿ_DC / _а = 0,064/ 0,05 = 1,3 мм.

На пересечении прямых, полученных графически аналогично ускорению точки а₃, получим точку d. Соединив ее с полюсом, получим отрезок [d], характеризующий ускорение точки d.

[d] = 27,9 мм., откуда, используя масштабный коэффициент:

a_D = [d] * _а = 27,9 * 0,05 = 1,4 м/с²

Касательные ускорения находим также из плана ускорений через длины отрезков:

a^_DE = [d] * _а = a_D = 1,4 м/с²

a^_DC = [dn₃] * _а = 28,2 * 0,05 = 1,41 м/с²

Далее определяем ускорения центров масс звеньев:

– ускорение центра масс звена 1 равно нулю, т.к. масса звена сосредоточена в точке О (полюс), а_S1 = 0;

– точка S₃ лежит на середине звена 3 (ВС), следовательно, соединив на плане ускорений середину отрезка [c] с полюсом, получим отрезок [s₃] характеризующий ускорение центра масс звена 3:

а_S3 = [s₃] * _а = 20,16 * 0,05 = 1 м/с²

– точка S₅ лежит на звене движущемся прямолинейно и поступательно, следовательно ускорения всех его точек будут одинаковы:

а_S5 = а_D = 1,4 м/с²

Определим угловые ускорения по формуле (2.2.1):

₃ = a^_A3B / l _A3B = 0,89 / 0,35 = 2,55 с^-1

₄ = a^_СD/ l_CD = 1,41 / 0,2 = 7,05 с^-1

Все рассчитанные величины заносим в таблицу 2.1

Таблица 2.1 – Значения скоростей и ускорений

V, м/с; , с-1;  с-2; а, м/с2	Положение = 1509
VA12	0,68
VA3	0,628
VC	0,874
VD	0,876
VA1A3	0.262
VCD	0,113
1	7,54
3	1,78
4	0,54
аА12	5,11
aA3B	0,89
atA3A1	3, 65
а3	1,44
ас	2,02
aD = аS5 = atDE	1,4
atDC	1,41
akA3A1	0,935
anA3В	1,13
anDC	0,064
аS3	1
1	1,67
3	2,55
4	7,05
aВ = anA3A1 = anDE= aE= аS1	0

Все построения приведены на лист 2 графической части курсового проекта.