2.8.1. Синтез кулисного механизма по заданному коэффициенту

изменения средней скорости и ходу выходного звена

Пример 2.7

Дано:

H - ход ползуна 5;

К- коэффициент изменения средней скорости;

L - расстояние между осями вращения кривошипа и кулисы.

Определить: длину кривошипа r, длину кулисы R, длину шатуна I и расстояние е.

Решение:

Длины звеньев механизма определяем исходя из крайних положений механизма. По коэффициенту К определим угол размаха кулисы β:

β=180˚∙(К-1) / (К+1).

Из ∆OA”C определим длину кривошипа:

r = L∙ sin(β/2) . (2.48)

Из ∆CFB” определим длину кулисы:

H

R = ———— . (2.49)

2∙sin(β/2)

Длину шатуна и расстояние e выбирают конструктивно, но так, чтобы угол давления а_тах не превышал 30^е.

Поэтому задаемся длиной шатуна / и определяем е:

e≤l∙sin а_тах (2.50)

2.8.2.Синтез механизма с вращающейся кулисой

Пример 2.9.

Дано:

H - ход ползуна;

К- коэффициент изменения средней скорости; О₁О=L

а_тах - максимальный угол давления;

λ=L/R- отношение длин звеньев.

Определить: длину кривошипа г, длину кулисы R, длину шатуна /.

Решение:

Рисунок 2.13 - Механизм с вращающейся кулисой

Представим схему механизма в двух крайних положениях. Из рисунка 2.8 видно, что:

R = L/ λ (2.51)

тогда угол холостого хода

φ_x = 360˚/(K+1) (2.52)

Из ∆O₁OA’ находим:

L

r = ———— (2.53)

cos(φ_x/2)

Длина шатуна:

R

l = ——— (2.54)

sin а_та

3.Кинематический анализ плоских механизмов аналитическим методом.

3.1 Определение положений звеньев методом векторного замкнутого контура.

При определении положений звеньев плоского рычажного механизма удобно применять метод векторных замкнутых контуров. Сущность этого метода заключается в следующем:

– звенья механизма изображают в виде векторов, которые образуют на схеме механизма один или несколько замкнутых векторных контуров;

– составляют для каждого векторного контура уравнение замкнутости в векторной форме;

– проектируя полученные уравнения на оси выбранной системы координат, получают аналитические зависимости параметров, характеризующих положение звеньев относительно обобщенной координаты механизма.

Рассмотрим суть этого метода на примере шарнирного четырехзвенника, изображенного на рисунке 3.1.

Представим каждое звено механизма в виде вектора. Выбор направлений векторов может быть произвольным, но если на звене есть неподвижная точка, то начало вектора целесообразно намечать в неподвижной точке. Например, вектора и 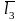выходят из неподвижных точек О и С соответственно, а направления векторов 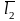и 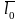могут быть заданы произвольно. Параметры, характеризующие положение всех звеньев механизма (₁, ₂, ₃, ₀), показывают в начале вектора от положительного направления одной из координатных осей, например оси х.

Чтобы записать условие замкнутости контура в векторной форме, необ­ходимо обойти периметр многоугольника в произвольно выбранном направлении и записать вектора этого направления со знаком «+», а направленные против обхода, со знаком «–».

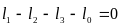^т.е.

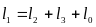^{. (3.1)}

Этому уравнению замкнутости в векторной форме соответствуют два уравнения проекций на оси координат:

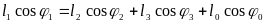^{; (3.2)}

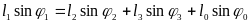^{. (3.3)}

Углы ₁ , ₂ и ₃ являются переменными параметрами, характеризующими соответственно положения звеньев 1, 2 и 3. Угол ₀ – постоянный параметр. При кинематическом анализе этого механизма должны быть заданы длины звеньев 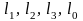и угол ₀,а также закон изменения угла ₁ (обобщенной координаты механизма). Таким образом, уравнения (2) и (3) имеют только два неизвестных параметра (₂ и ₃), которые можно определить при совместном решении этих уравнений.