2.7.1. Синтез кривошипно-ползунного механизма по коэффициенту изменения средней скорости и ходу ползуна
Пример 2.5
Дано:
H- ход ползуна;
К- коэффициент изменения средней скорости;
λ = r/l -отношение длин звеньев.
Рекомендуется: λ =(1/3,5) + (1/4,5).
Максимальный угол давления будет в положении ОА*B*, когда кривошип перпендикулярен направлению движения ползуна. αmах не должен превышать 30°.
Определить: длину кривошипа г, длину шатуна /, величину дезаксиала
Рисунок 2.11 - Кривошишо-ползунный механизм
Решение:
По коэффициенту изменения средней скорости К определим угол θ между крайними положениями шатуна:
θ=180˚∙(К-1) / (К+1). (2.39)
Длину звеньев механизма определим, исходя из крайних положений механизма.
Из
∆О
В'В" запишем:
Н2 = (г +l)2 +(l-r)2 - 2(l+ г)(l - г) cosθ
Н2 =l2 +2lг +г2 +/2 -2!r + r2 -2(l2 -r2) cosθ
H2 = 2l2 + 2lr2-2{l2-r2)cosθ.
Подставим r =λ∙l
H2 =2[l2 + λ2!2 -!2(1-λ2) cosθ].
Тогда
l=H/ (√2[1 + λ2 – (1 - λ2)∙ cosθ]).
Из ∆OCB” находим:
e = (l+r)sinα”.
Из ∆OB’B” следует:
sinα” l- r
—— = —— ,
sinθ H
отсюда
l- r
sinα” = —— - sinθ
H
Тогда
l2- r2
e = —— sinθ . (2.40)
H
2.7.2. Синтез кривошипно-ползунного механизма по заданному ходу ползуна и максимальным углам давления рабочего и холостого ходов
Пример 2.6
Дано:
H-ход ползуна;
αp max, αx max – максимальные углы давления на рабочем и холостом ходу.
Определить: длину кривошипа г, длину шатуна /, величину дезаксиала е (рисунок 2.12).
Решение:
Введем обозначения: λ = r/l, δ = e/l. (2.41)
Из ∆OB’D определим:
DB’= √(OB’)2 - OD2
или
DB’= √(l- r) 2 - e2 .
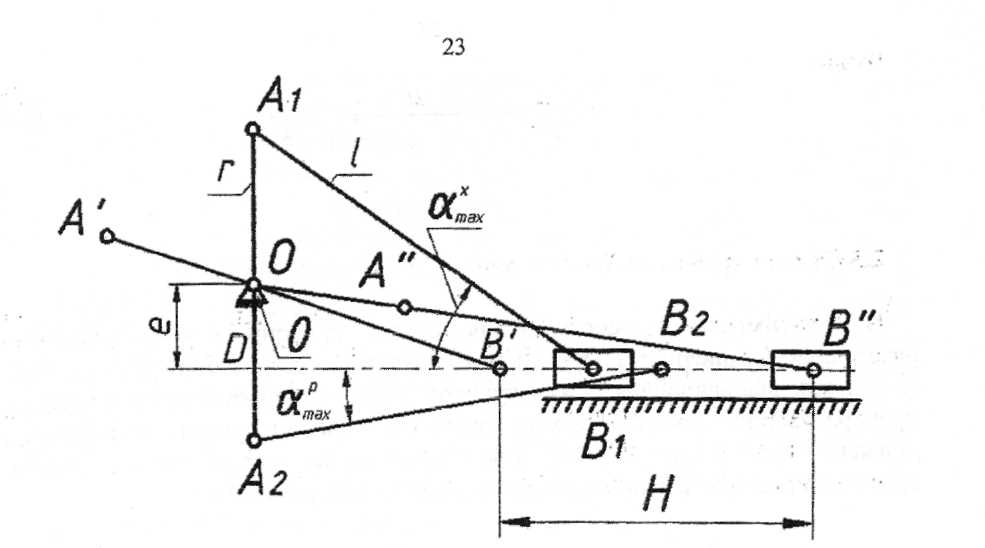
Рисунок 2.12 - Кривошипно-ползунный механизм
Из ∆OB”D: DB”= √(OB”)2 - OD2
или DB”= √(l- r) 2 - e2 .
Тогда H=DB” – DB’
или H=√(l+ r) 2 - e2 - √(l- r) 2 - e2
H=
l(√(1+
λ)
2
- δ2
-
√(1- λ)
2
- δ2
)
. (2.42)
Углы давления: sin αp max = λ- δ; (2.43)
sin αx max = λ+ δ. (2.44)
Решая совместно уравнения (2.43) и (2.44) определим:
sin αx max + sin αp max
λ = ———————— ; (2.45)
2
sin αx max - sin αp max
δ = ———————— ; (2.46)
2
Тогда H
l= ——————————— (2.47)
√(1+ λ) 2 - δ2 - √(1- λ) 2 - δ2 )
2.8. Синтез кулисных механизмов
В зависимости от соотношения длины кривошипа r и межосевого расстояния L (рисунок 2.13) кулисные механизмы могут быть с качающейся (г<1.) или вращающейся (r>L) кулисой. Тогда в первом случае происходит преобразование вращательного движения кривошипа в колебательное движение кулисы (рисунок 2.13), а во втором случае - вращательное движение кривошипа во вращательное движение кулисы (рисунок 2.14).
Рисунок 2.12 - Кулисный механизм