Контрольные вопросы
1. Дайте определение случайной величины.
2. Какая с.в. называется дискретной (непрерывной)? Приведите примеры.
3. Что такое закон распределения случайной величины?
4. Что называется рядом распределения дискретной случайной величины?
5. Что такое функция распределения случайной величины? Какими свойствами она обладает?
6. Что называется функцией плотности распределения вероятностей случайной величины? Перечислите её свойства.
7. Чем различаются графики функций распределения дискретной и непрерывной случайных величин?
8. Что называется математическим ожиданием непрерывной и дискретной случайных величин? Что оно характеризует? Какими свойствами оно обладает? Какие ещё числовые характеристики случайных величин вам известны?
9. Дайте определение дисперсии случайной величины, перечислите её свойства. Что она характеризует?
10. Как определяются математическое ожидание и дисперсия для биномиального, равномерного, показательного, нормального распределений?
Лабораторная работа 3 Линейная регрессия
Цель работы: получить навыки построения регрессионных моделей с помощью системы Maple.
Краткий теоретический материал. Парная регрессия – уравнение связи двух переменных:
,
где
–
зависимая переменная (результативный
признак);
–
независимая
объясняющая переменная (фактор-признак).
Линейная
парная регрессия:
,
где
и
− параметры регрессии,
− случайная переменная или ошибка.
Построение уравнения
регрессии сводится к оценке её
параметров. Для этого используют метод
наименьших квадратов (МНК).
МНК позволяет получить такие оценки
параметров, при которых сумма квадратов
отклонений фактических значений
результативного признака
от теоретических значений
минимальна, т.е.:
.
Для нахождения оценок параметров регрессии решается следующая система относительно и :
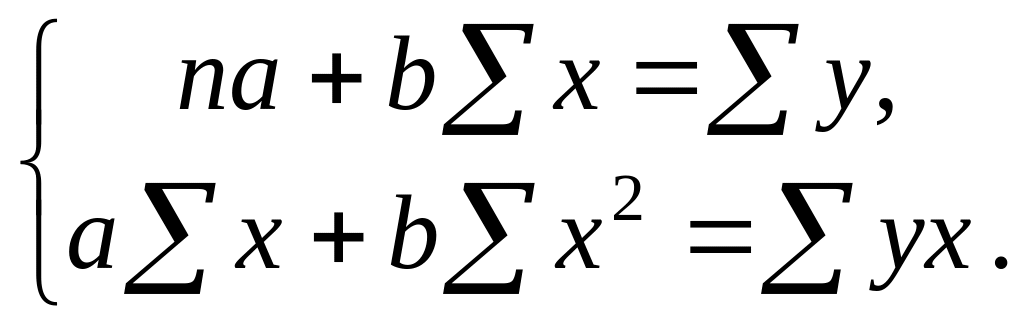
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
,
где
−
общая сумма квадратов отклонений;
–
сумма квадратов
отклонений, обусловленная регрессией
(«объяснённая» или «факторная»);
–
остаточная сумма
квадратов отклонений.
Долю дисперсии,
объясняемую регрессией, в общей дисперсии
результативного признака
характеризует коэффициент детерминации
,
который можно вычислить по формуле:
.
Например, коэффициент
детерминации
свидетельствует о том, что вариация
исследуемой зависимой переменной
на 87,1 % объясняется изменчивостью
объясняющей переменной
.
Уравнение регрессии
значимо на уровне
,
если фактическое значение
– статистики
удовлетворяет
условию
,где
− табличное значение
-критерия
Фишера;
− число оцениваемых параметров уравнения
регрессии (для линейной парной регрессии
);
− число наблюдений;
,
.
Задание. Рассматриваются случайные величины X и Y, между которыми существует статистическая зависимость. Случайная ве-личина X считается независимой переменной, Y – зависимой. По заданным в условии результатам измерения аппроксимировать статистическую зависимость подходящей линейной зависимостью. Уравнение прямой найти методом наименьших квадратов. Определить достоверность полученной зависимости.
Вариант 1
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-1.45 |
-1.83 |
-1.25 |
-1.05 |
-1.24 |
-0.99 |
-0.77 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
-0.50 |
-0.34 |
0.08 |
0.09 |
0.32 |
0.99 |
0.86 |
Вариант 2
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-2.17 |
-1.38 |
-0.97 |
-0.5 |
-0.31 |
-0.72 |
-0.31 |
x |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
0.4 |
y |
0.2 |
0.92 |
0.99 |
1.05 |
1.30 |
1.41 |
1.89 |
Вариант 3
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
0.49 |
0.63 |
0.28 |
0.77 |
1.3 |
1.21 |
1.31 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
1.46 |
1.91 |
2.15 |
2.28 |
2.43 |
2.73 |
2.57 |
Вариант 4
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-0.14 |
0.66 |
1.40 |
0.93 |
1.74 |
1.76 |
1.77 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
2.62 |
2.79 |
2.74 |
2.72 |
3.31 |
3.50 |
4.08 |
Вариант 5
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
2.02 |
2.07 |
2.44 |
2.71 |
2.96 |
2.91 |
3.32 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
3.49 |
3.46 |
3.97 |
4.12 |
3.94 |
4.68 |
4.92 |
Вариант 6
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
2.32 |
2.45 |
2.92 |
2.54 |
3.49 |
3.73 |
4.11 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
4.94 |
4.68 |
4.86 |
5.61 |
6.02 |
5.46 |
6.59 |
Вариант 7
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
3.91 |
3.89 |
4.70 |
4.99 |
4.94 |
5.48 |
5.38 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
5.49 |
5.4 |
5.71 |
6.52 |
6.35 |
6.52 |
7.14 |
Вариант 8
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
3.97 |
4.81 |
4.92 |
5.36 |
5.82 |
5.79 |
6.27 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
6.86 |
6.21 |
6.86 |
7.37 |
7.53 |
7.96 |
8.40 |
Вариант 9
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
2.26 |
1.68 |
1.48 |
1.27 |
1.18 |
1.13 |
0.65 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
0.74 |
0.22 |
0.22 |
0.02 |
-0.38 |
-0.57 |
-0.92 |
Вариант 10
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
2.71 |
2.85 |
2.34 |
2.4 |
1.76 |
2.16 |
1.81 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
1.6 |
1.14 |
1.35 |
0.79 |
0.99 |
0.27 |
0.06 |
Вариант 11
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
4.09 |
3.64 |
3.43 |
3.19 |
3.10 |
3.06 |
2.68 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
2.24 |
2.26 |
2.04 |
1.96 |
1.19 |
1.50 |
1.04 |
Вариант 12
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
4.59 |
4.78 |
4.49 |
4.20 |
3.75 |
3.94 |
3.54 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
3.62 |
3 |
2.78 |
2.77 |
2.51 |
2.48 |
1.80 |
Вариант 13
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
5.89 |
5.34 |
5.62 |
5.19 |
4.75 |
4.65 |
4.25 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
4.25 |
4.23 |
3.96 |
3.82 |
3.56 |
3.24 |
2.89 |
Вариант 14
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
7.69 |
7.51 |
7.31 |
6.95 |
6.63 |
6.52 |
5.65 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
5.61 |
5.08 |
4.77 |
4.50 |
4.22 |
3.35 |
3.87 |
Вариант 15
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
4.87 |
4.99 |
5.07 |
5.44 |
5.36 |
5.43 |
5.50 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
5.64 |
5.86 |
5.79 |
5.92 |
6.36 |
6.08 |
6.5 |
Вариант 16
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-1.46 |
-1.84 |
-1.26 |
-1.06 |
-1.25 |
-0.98 |
-0.78 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
-0.51 |
-0.35 |
0.09 |
0.08 |
0.33 |
0.98 |
0.87 |
Вариант 17
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-2.18 |
-1.39 |
-0.98 |
-0.6 |
-0.32 |
-0.73 |
-0.32 |
x |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
0.4 |
y |
0.21 |
0.93 |
0.98 |
1.06 |
1.31 |
1.42 |
1.88 |
Вариант 18
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
0.48 |
0.64 |
0.29 |
0.78 |
1.31 |
1.23 |
1.32 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
1.47 |
1.9 |
2.14 |
2.29 |
2.44 |
2.72 |
2.56 |
Вариант 19
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
-0.15 |
0.67 |
1.41 |
0.94 |
1.75 |
1.76 |
1.78 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
2.62 |
2.79 |
2.74 |
2.72 |
3.31 |
3.50 |
4.08 |
Вариант 20
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
y |
2.02 |
2.07 |
2.44 |
2.71 |
2.96 |
2.91 |
3.32 |
x |
-0.2 |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
y |
3.49 |
3.46 |
3.97 |
4.12 |
3.94 |
4.68 |
4.92 |
Вариант 21
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
2.33 |
2.46 |
2.91 |
2.54 |
3.48 |
3.74 |
4.12 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
4.95 |
4.69 |
4.86 |
5.62 |
6.03 |
5.45 |
6.58 |
Вариант 22
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
3.91 |
3.89 |
4.70 |
4.99 |
4.94 |
5.48 |
5.38 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
5.49 |
5.4 |
5.71 |
6.52 |
6.35 |
6.52 |
7.14 |
Вариант 23
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
3.97 |
4.81 |
4.92 |
5.36 |
5.82 |
5.79 |
6.27 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
6.86 |
6.21 |
6.86 |
7.37 |
7.53 |
7.96 |
8.40 |
Вариант 24
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
2.26 |
1,68 |
1.48 |
1.27 |
1.18 |
1.13 |
0.65 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
0.74 |
0.22 |
0.22 |
0.02 |
-0.38 |
-0.57 |
-0.92 |
Вариант 25
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
2.71 |
2.85 |
2.34 |
2.4 |
1.76 |
2.16 |
1.81 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
1.6 |
1.14 |
1.35 |
0.79 |
0.99 |
0.27 |
0.06 |
Вариант 26
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
4.09 |
3.64 |
3.43 |
3.19 |
3.10 |
3.06 |
2.68 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
2.24 |
2.26 |
2.04 |
1.96 |
1.19 |
1.50 |
1.04 |
Вариант 27
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
4.59 |
4.78 |
4.49 |
4.20 |
3.75 |
3.94 |
3.54 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
3.62 |
3 |
2.78 |
2.77 |
2.51 |
2.48 |
1.80 |
Вариант 28
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
5.89 |
5.34 |
5.62 |
5.19 |
4.75 |
4.65 |
4.25 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
4.25 |
4.23 |
3.96 |
3.82 |
3.56 |
3.24 |
2.89 |
Вариант 29
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
7.69 |
7.51 |
7.31 |
6.95 |
6.63 |
6.52 |
5.65 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
5.61 |
5.08 |
4.77 |
4.50 |
4.22 |
3.35 |
3.87 |
Вариант 30
x |
-0.11 |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
y |
4.87 |
4.99 |
5.07 |
5.44 |
5.36 |
5.43 |
5.50 |
x |
-0.3 |
-0.2 |
-0.1 |
0. |
0.1 |
0.2 |
0.3 |
y |
5.64 |
5.86 |
5.79 |
5.92 |
6.36 |
6.08 |
6.5 |
Пример выполнения лабораторной работы
Зададим
значения величин
и
.
> restart:X:=[-0.9,-0.8,-0.7,-0.6,-0.5,-0.4,-0.3,-0.2, -0.1,0,0.1,0.2,0.3,0.4]:
>Y:=[-5.32,-5.62,-5.51,-4.72,-4.68,-4.24,-3.74,-3.46,-2.84,-3.39,-3.08,-2.17,-1.69,-1.33]:
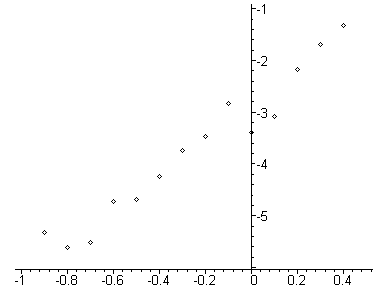
Построим
корреляционное поле. Нанесём точки с
координатами
,
на координатную плоскость.
> with(stats): statplots[scatterplot](X,Y,color=black);
Замечание. В версии Maple V R 4 для построения корреляционного поля нужно вызывать функцию с именем scatter 2d.
Методом
наименьших квадратов найдём прямую
такую,
что сумма квадратов отклонений заданных
точек от прямой будет наименьшей.
> fit[leastsquare[[x,y]]]([X,Y]);
Результат, полученный на экране монитора:
Для удобства определим найденную зависимость как функцию пользователя с именем :
> F:=unapply(-2.888461538+3.243296703*x,x);
Результат, полученный на экране монитора:
Определим
«значимость» полученной нами регрессионной
зависимости. Вычислим значение
коэффициента детерминации R2.
Найдём среднее значение
.
Обозначим эту величину идентификатором
Ysr.
> n:=14:Ysr:=sum(Y[i],'i'=1..n)/n;
Результат, полученный на экране монитора:
Вычислим
значения
,
определяемые уравнением регрессии.
Полученное множество значений обозначим
идентификатором FL.
> FL:=seq(F(X[i]),i=1..n):
Определим
– меру
разброса, объяснённого с помощью
регрессии, и
– меру
общего разброса (вариации) переменной
:
> SR2:=sum((FL[i]-Ysr)^2,'i'=1..n); S2:=sum((Y[i]-Ysr)^2,'i'=1..n);
Результат, полученный на экране монитора:
Вычислим значение статистического коэффициента детерминации R2:
> R2:=SR2/S2;
Результат, полученный на экране монитора:
По величине коэффициента детерминации заключаем, что вариация исследуемой зависимой переменной на 95.13 % объясняется изменчивостью объясняющей переменной х.
Определим значимость уравнения регрессии. Найдём Fst –зна-чение F-статистики:
> Fst:=R2*(n-2)/(1-R2);
Результат, полученный на экране монитора:
Найденное значение Fst сравним с критическим значением критерия Фишера. Уровень значимости примем равным 0.05. По таблице определяем, что Fкр=4.747. Так как Fst>Fкр, то уравнение регрессии значимо на уровне 0.05.
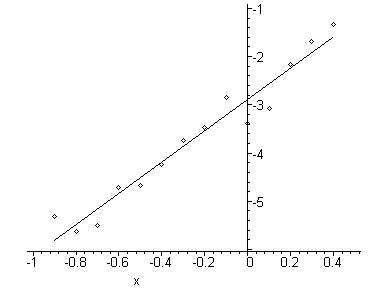
Изобразим корреляционное поле и график полученной прямой на одном рисунке:
> k:=statplots[scatterplot](X,Y,color=green):
> l:=plot(F(x),x=-0.9..0.4):
> plots[display]([k,l]);
Результат, полученный на экране монитора:
