- •Часть 2
- •Режим доступа к электронному аналогу печатного издания: http://www.Libdb.Sssu.Ru
- •Содержание
- •Предисловие
- •Лабораторная работа 1
- •Варианты заданий
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
- •Лабораторная работа 2 Исследование дискретной и непрерывной случайных величин
- •Пример выполнения задания 1
- •Контрольные вопросы
- •Лабораторная работа 3 Линейная регрессия
- •Контрольные вопросы
- •1 Доверительный интервал для м.О. Нормально распределённой с.В.
- •2 Доверительный интервал для дисперсии нормально распределённой г.С.
- •Проверка статистических гипотез
- •1. Предварительная обработка реализации выборки
- •F*(X) – статистическая функция распределения; f(X) – функция распределения
- •2. Основные понятия проверки статистических гипотез
- •3. Критерий согласия
- •Контрольные вопросы к лабораторным работам 4 и 5
- •Библиографический список
- •Приложение 5 (справочное) Критические точки распределения Стьюдента
- •Часть 2
- •3 46500, Г. Шахты, Ростовская обл., ул. Шевченко, 147
3. Критерий согласия
Критерием согласия называют критерии проверки статистических гипотез о виде закона распределения г.с. Примером статистической гипотезы о виде закона распределения г.с. X является: «Г.с. X имеет нормальный (равномерный и т.д.) закон распределения». Такая гипотеза принимается за основную гипотезу H0.
Рассмотрим подробно эффективный критерий согласия Пир-сона .
Пусть проверяется
гипотеза «Г.с. X
имеет
гипотетическую функцию распределения
![]() »,
где
»,
где
![]() –
неизвестные параметры распределения,
вид функции F
известен, l
1.
Рассмотрим случай непрерывного
распределения.
–
неизвестные параметры распределения,
вид функции F
известен, l
1.
Рассмотрим случай непрерывного
распределения.
На первом этапе
по реализации выборки объёма n
строится интервальный статистический
ряд с k
= [1+3.32lg
n]
+1 частичными промежутками (см. п. 1). Пусть
получены равные промежутки с границами
в точках
![]() .
Рассмотрим промежутки:
.
Рассмотрим промежутки:
![]() .
(3)
.
(3)
Пусть по выборке найдены точечные оценки неизвестных параметров (методом максимального правдоподобия). Тогда при помощи гипотетической функции распределения можно найти вероятности
![]()
![]() (4)
(4)
![]() .
.
Известно, что при достаточно больших значениях объёма выборки n случайная величина
![]() (5)
(5)
имеет распределение,
близкое к распределению
![]() (хи-
квадрат) со
степенью свободы
s = k– l – 1,
где k –
число интервалов, l
– число
неизвестных параметров, заменённых их
точечными оценками, mi
– частота
i-го
интервала. Если основная гипотеза верна,
то величина npi
будет близка к частоте ni,
т.е. сумма
(хи-
квадрат) со
степенью свободы
s = k– l – 1,
где k –
число интервалов, l
– число
неизвестных параметров, заменённых их
точечными оценками, mi
– частота
i-го
интервала. Если основная гипотеза верна,
то величина npi
будет близка к частоте ni,
т.е. сумма
![]() будет мала. В качестве статистики
критерия выбирается случайная величина
будет мала. В качестве статистики
критерия выбирается случайная величина
![]() .
Тогда при заданном уровне значимости
основная гипотеза отвергается, когда
.
Тогда при заданном уровне значимости
основная гипотеза отвергается, когда
![]() .
Это равенство эквивалентно
.
Это равенство эквивалентно
![]() .
А это означает, что
.
А это означает, что
![]() – квантиль распределения
– квантиль распределения
![]() порядка
1–
со степенью свободы
s =
k– l – 1.
порядка
1–
со степенью свободы
s =
k– l – 1.
Таким образом,
если выборочное значение
![]() статистики
статистики
![]() окажется меньше квантили
окажется меньше квантили
![]() ,
то основная гипотеза принимается.
,
то основная гипотеза принимается.
Сформулируем кратко критерий проверки гипотезы о виде закона распределения г.с.
1) По данной реализации выборки построить интервальный статистический ряд, найти промежутки (3).
2) Вычислить по реализации выборки точечные оценки неизвестных параметров .
3) Вычислить величины npi (i = 1, …, k) по формулам (4). Проверить выполнение условий npi 5. Если для некоторых интервалов это условие нарушается, то этот интервал объединяется с соседним (при этом складываются вероятности pi и частоты этих интервалов). Эта процедура продолжается до тех пор, пока для всех интервалов не будет выполняться условие npi 5.
4) По формуле (5)
вычислить выборочное значение![]() статистики
.
статистики
.
5) По таблице найти
квантиль
![]() распределения
порядка 1–
со степенью свободы
s =
k– l – 1, где
k –
число интервалов после пересчёта в
пункте 3, l –
число
неизвестных параметров, заменённых их
точечными оценками в пункте 2.
распределения
порядка 1–
со степенью свободы
s =
k– l – 1, где
k –
число интервалов после пересчёта в
пункте 3, l –
число
неизвестных параметров, заменённых их
точечными оценками в пункте 2.
6) Если < , то основная гипотеза принимается на уровне значимости ; если , то основная гипотеза отвергается.
Статистические вычисления в Maple
Пакет stats поддерживает разнообразные статистические вычисления и включает в себя следующие подпакеты:
describe − содержит функции для вычисления статистических характеристик данных;
fit − для регрессионного анализа (аппроксимации данных заданными зависимостями);
transform − для преобразования статистических данных;
random − для генерирования случайных массивов данных с заданными свойствами;
statevalf − для получения численных оценок массивов данных;
statplots − для графического представления данных.
Задание. Для изучения некоторой дискретной случайной величины из генеральной совокупности была извлечена выборка объёма .
Получить статистический ряд частот и относительных частот выборки.
Определить накопленные частоты и накопленные относительные частоты.
Построить полигон частот и кумуляту выборки.
Записать эмпирическую функцию распределения и построить её график.
Получить выборочное среднее, моду, медиану, выборочную дисперсию, несмещённую выборочную дисперсию, выборочное сред-неквадратическое отклонение.
Варианты заданий
0, 3, 1, 2, 2, 0, 3, 3, 0, 1, 3, 2, 2, 1, 0, 3, 1, 1, 3, 0, 2, 2, 3, 2, 3, 2, 1, 3, 1, 3, 0, 3, 1, 0, 0, 2, 0, 2, 0, 1;
3, 3, 1, 3, 1, 1, 1, 3, 1, 3, 1, 1, 3, 1, 4, 4, 3, 1, 4, 1, 2, 2, 4, 2, 2, 4, 3, 1, 4, 3, 4, 4, 4, 3, 1, 1, 3, 1, 2, 2;
4, 5, 2, 4, 2, 3, 4, 4, 5, 4, 5, 5, 4, 2, 2, 5, 2, 5, 2, 5, 5, 5, 5, 3, 5, 3, 5, 2, 2, 4, 4, 3, 3, 4, 3, 4, 4, 5, 3, 3;
5, 4, 6, 4, 3, 3, 3, 4, 5, 3, 4, 6, 4, 3, 3, 5, 6, 5, 5, 5, 3, 3, 4, 6, 4, 5, 5, 5, 3, 6, 3, 4, 3, 6, 6, 4, 3, 4, 6, 5;
5, 7, 6, 7, 7, 7, 4, 5, 5, 7, 7, 6, 4, 5, 5, 4, 5, 4, 7, 7, 5, 5, 7, 7, 5, 6, 6, 5, 7, 7, 7, 7, 7, 6, 7, 5, 5, 4, 7, 6;
5, 5, 6, 5, 5, 7, 8, 5, 8, 6, 8, 6, 7, 5, 6, 8, 7, 5, 8, 7, 7, 7, 8, 8, 8, 6, 6, 5, 5, 7, 5, 8, 7, 5, 5, 8, 7, 6, 5, 5;
6, 7, 8, 7, 7, 8, 7, 6, 8, 7, 8, 7, 6, 8, 8, 8, 7, 9, 9, 7, 7, 7, 9, 7, 6, 9, 6, 7, 7, 7, 6, 7, 6, 9, 8, 9, 8, 8, 6, 6;
8, 10, 8, 9, 8, 9, 8, 7, 10, 7, 8, 7, 7, 10, 8, 7, 9, 9, 10, 8, 8, 8, 10, 9, 7, 7, 10, 10, 9, 7, 7, 9, 7, 9, 10, 8, 7, 7, 10, 7;
9, 10, 9, 9, 8, 8, 11, 11, 9, 8, 9, 11, 9, 10, 9, 11, 8, 9, 10, 10, 8, 8, 8, 9, 10, 10, 9, 10, 10, 11, 9, 11, 8, 9, 11, 8, 10, 10, 11, 11;
12, 10, 10, 10, 10, 10, 12, 12, 12, 12, 10, 12, 12, 10, 9, 11, 10, 11, 9, 9, 9, 11, 12, 11, 9, 10, 10, 12, 11, 12, 12, 9, 10, 10, 9, 9, 10, 11, 12, 10;
13, 11, 10, 10, 11, 10, 11, 12, 11, 12, 12, 12, 10, 13, 10, 12, 10, 11, 11, 10, 10, 13, 11, 10, 13, 12, 12, 13, 12, 11, 12, 10, 11, 10, 13, 10, 13, 10, 13, 12;
13, 14, 12, 13, 14, 11, 13, 13, 11, 13, 13, 13, 12, 12, 11, 12, 14, 14, 11, 13, 12, 14, 11, 13, 12, 14, 13, 11, 11, 12, 11, 12, 11, 13, 11, 12, 13, 13, 11, 13;
14, 14, 15, 12, 14, 12, 14, 14, 14, 14, 13, 13, 15, 15, 12, 13, 12, 14, 14, 12, 12, 13, 14, 13, 12, 13, 13, 15, 14, 12, 14, 14, 14, 14, 13, 12, 14, 12, 15, 12;
15, 15, 14, 16, 13, 16, 15, 13, 15, 16, 15, 14, 14, 16, 13, 13, 15, 15, 15, 13, 15, 16, 14, 16, 16, 14, 13, 16, 13, 14, 14, 16, 15, 13, 13, 15, 15, 13, 13, 16;
17, 15, 17, 15, 14, 15, 16, 14, 17, 15, 16, 14, 15, 16, 16, 14, 15, 15, 15, 14, 15, 17, 14, 17, 15, 17, 16, 15, 14, 15, 17, 16, 15, 17, 14, 16, 17, 17, 14, 17;
17, 16, 18, 16, 18, 15, 18, 17, 17, 16, 17, 17, 16, 16, 16, 18, 16, 17, 17, 16, 18, 17, 17, 16, 16, 18, 17, 18, 17, 18, 16, 17, 18, 16, 15, 18, 16, 16, 17, 18;
17, 16, 18, 18, 19, 18, 19, 17, 19, 16, 17, 16, 18, 17, 19, 19, 16, 18, 16, 18, 17, 17, 17, 16, 18, 17, 18, 18, 17, 18, 19, 17, 17, 18, 19, 18, 17, 17, 17, 17;
17, 19, 17, 19, 19, 20, 19, 17, 17, 18, 20, 19, 19, 19, 19, 18, 18, 19, 20, 20, 19, 19, 19, 19, 18, 19, 17, 18, 18, 19, 17, 18, 19, 17, 18, 20, 19, 19, 20, 17;
21, 20, 18, 19, 21, 21, 18, 18, 21, 20, 21, 21, 19, 19, 21, 21, 19, 21, 21, 18, 19, 18, 18, 18, 19, 21, 19, 21, 19, 19, 21, 18, 18, 19, 20, 19, 18, 20, 21, 19;
20, 22, 21, 21, 21, 21, 19, 22, 20, 20, 22, 22, 22, 20, 19, 20, 20, 22, 21, 21, 22, 19, 22, 21, 22, 22, 22, 22, 22, 21, 22, 22, 20, 19, 20, 19, 22, 21, 20, 19;
20, 21, 23, 22, 21, 20, 22, 21, 21, 20, 23, 23, 22, 22, 22, 20, 23, 20, 22, 20, 21, 22, 21, 22, 22, 22, 20, 21, 20, 22, 20, 21, 22, 22, 22, 22, 20, 23, 23, 23;
21, 22, 22, 21, 22, 23, 24, 23, 24, 23, 24, 24, 23, 24, 23, 24, 24, 23, 23, 24, 21, 23, 24, 21, 21, 22, 23, 24, 21, 21, 24, 23, 23, 21, 23, 21, 23, 23, 23, 21;
24, 23, 23, 22, 24, 23, 25, 23, 25, 24, 25, 24, 25, 24, 24, 25, 25, 25, 23, 23, 24, 25, 24, 22, 23, 22, 25, 25, 24, 24, 23, 25, 23, 22, 22, 22, 22, 23, 24, 25;
23, 25, 25, 24, 24, 23, 26, 26, 23, 26, 23, 24, 24, 25, 24, 23, 24, 25, 26, 24, 25, 24, 24, 26, 24, 25, 25, 23, 25, 26, 26, 25, 25, 25, 23, 26, 26, 25, 24, 23;
25, 27, 26, 26, 25, 27, 26, 25, 24, 27, 27, 24, 27, 26, 26, 24, 24, 25, 24, 26, 27, 24, 24, 27, 25, 26, 27, 26, 27, 27, 26, 27, 24, 24, 26, 24, 25, 27, 27, 27;
28, 27, 28, 25, 27, 25, 25, 25, 28, 26, 27, 25, 25, 25, 26, 25, 26, 28, 25, 27, 27, 28, 27, 26, 25, 28, 25, 26, 25, 25, 27, 25, 25, 28, 28, 25, 28, 27, 25, 27;
27, 28, 26, 28, 27, 28, 28, 29, 27, 27, 28, 29, 28, 28, 27, 27, 28, 28, 28, 29, 27, 29, 26, 26, 26, 29, 29, 28, 26, 29, 26, 29, 28, 27, 27, 28, 27, 28, 29, 27;
30, 28, 30, 28, 27, 28, 27, 29, 28, 28, 30, 27, 29, 27, 30, 28, 28, 27, 30, 28, 27, 28, 27, 27, 27, 28, 28, 30, 28, 27, 29, 29, 29, 30, 28, 29, 28, 27, 28, 27;
30, 29, 28, 31, 28, 30, 30, 31, 28, 28, 31, 30, 28, 31, 29, 28, 31, 31, 31, 29, 30, 31, 30, 28, 31, 29, 30, 29, 30, 28, 28, 31, 29, 31, 28, 28, 30, 28, 29, 30;
30, 31, 32, 29, 30, 32, 31, 29, 30, 32, 30, 30, 30, 32, 32, 31, 32, 31, 32, 30, 30, 29, 30, 31, 32, 30, 31, 31, 29, 32, 29, 30, 30, 30, 29, 30, 30, 32, 31, 31.
Пример выполнения работы
Загрузим пакет stats и подпакеты transform, describe.
> with(stats): with(transform):with(describe):
Введём выборку
![]() :
:
>X:=[39,41,40,42,41,40,42,44,40,43,42,41,43,39,42,41,42,39,41,37,43,41,38,43,42,41,40,41,38,44,40,39,41,40,42,40,41,42,40,43,38,39,41,41,42];
X:=[39,41,40,42,41,40,42,44,40,43,42,41,43,39,42,41,42,39,41,37,43,41, 38,43,42,41,40,41,38,44,40,39,41,40,42,40,41,42,40,43,38,39,41,41,42].
Определим объём выборки (подсчитаем количество значений в выборке):
> n:=count(X);
n=45
Построим статистический ряд частот (варианты расположим в порядке возрастания и каждой варианте поставим в соответствие её частоту − число, показывающее, сколько раз данная варианта встречается в выборке).
> X1:=tally(X);
![]()
![]() .
.
Если работа выполняется в Maple V, R4, то варианты могут оказаться расположенными в произвольном порядке, необходимо ряд переписать так, чтобы они были расположены по возрастанию.
> X2:= statsort(X1);
.
Получим статистический ряд относительных частот (каждой варианте поставим в соответствие её относительную частоту, т.е. частоту, делённую на объём выборки).
> X3:= scaleweight[1/n](X2);
.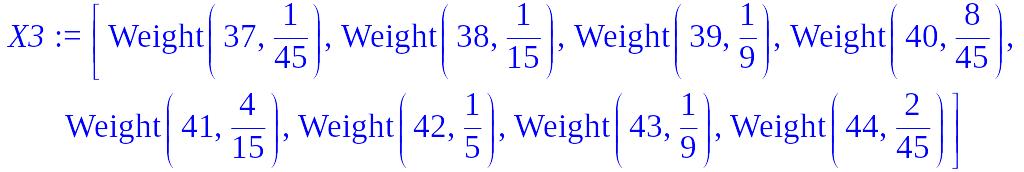
Найдём накопленные частоты. Накопленная частота показывает, сколько наблюдалось значений, меньших заданного x:
> X4:=cumulativefrequency(X2);
.![]()
Найдём относительные накопленные частоты:
> X5:=cumulativefrequency(X3);
.![]()
Построим полигон частот. На координатной плоскости отметим точки, абсциссами которых являются варианты, а ординатами – их частоты, и соединим эти точки последовательно отрезками прямых:
> a:=plots[pointplot]([[37,1],[38,3],[39,5],[40,8],[41,12],[42,9],[43,5],
[44,2]]):> b:=plot([[37,1],[38,3],[39,5],[40,8],[41,12],[42,9],[43,5],[44,2]]):
> plots[display]([a,b]);

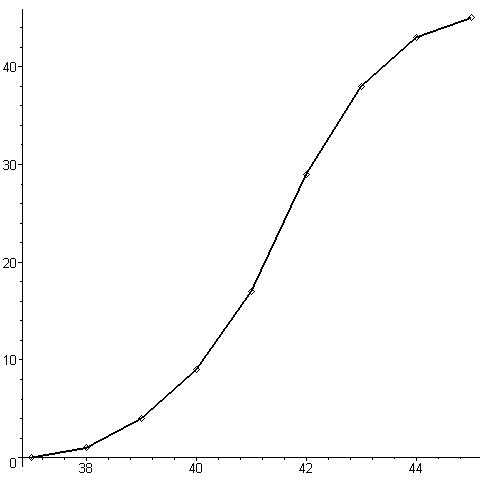
Построим кумуляту. На координатной плоскости построим точки, абсциссами которых являются варианты, а ординатами – их накопленные частоты, и соединим эти точки отрезками прямых:
a1:=plots[pointplot]([[37,0],[38,X4[1]],[39,X4[2]],[40,X4[3]],[41,X4[4]],[42,X4[5]],[43,X4[6]],[44,X4[7]],[45,X4[8]]], color=black):
b1:=plot([[37,0],[38,X4[1]],[39,X4[2]],[40,X4[3]],[41,X4[4]],[42,X4[5]],[43,X4[6]], [44,X4[7]],[45,X4[8]]],color=green):
plots[display]([a1,b1]);
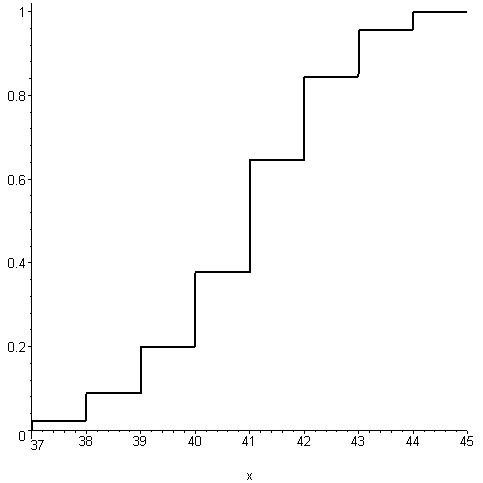
Запишем эмпирическую функцию распределения.
> F:=piecewise(x<=37,0,x>37 and x<=38,X5[1],x>38 and x<=39,X5[2],x>39 and x<=40,X5[3],x>40 and x<=41,X5[4],x>41 and x<=42,X5[5],x>42 and x<=43,X5[6],x>43 and x<=44,X5[7],x>44,X5[8]);

Теперь построим её график.
> plot(F,x=37..45,color=blue);
Найдем выборочную среднюю и её значение в виде числа с плавающей точкой:
> M:=mean(X);evalf(M);
M:=613/15
40.86666667
Определим выборочную моду:
> mode(X);
41
Определим выборочную медиану:
> median(X);
41
Найдём выборочную дисперсию:
>S:=variance(X);evalf(S);
S:=586/225
2.604444444
Найдём несмещённую выборочную дисперсию:
> S1:=n/(n-1)*S; evalf(S1);
S1:=293/110
2.663636364
Вычислим среднеквадратическое отклонение (корень квадратный из дисперсии):
> sigma:=standarddeviation(X);evalf(sigma);
![]()
1.613829125
Лабораторная работа 5
Обработка результатов экспериментов, определение точечных оценок числовых характеристик и параметров распределения.
Проверка гипотезы о законе распределения
генеральной
совокупности по критерию согласия
![]()
Цель работы: выработать практические навыки элементарной статистической обработки результатов экспериментов. Научиться поль-зоваться критерием согласия Пирсона для проверки гипотезы о виде распределения генеральной совокупности.
Задание. Для изучения некоторой случайной величины из генеральной совокупности была извлечена выборка объёма n = 80 (см. данные своего варианта).
Определить число отрезков разбиения, построить интервальный статистический ряд. Построить гистограмму относительных частот и график эмпирической функции распределения.
Выдвинуть гипотезу о виде распределения. Найти состоятельные несмещённые оценки математического ожидания и дисперсии, оценки среднеквадратического отклонения, оценки параметров распределения.
Проверить выдвинутую гипотезу по критерию Пирсона на уровне значимости α =0,01.
На одном рисунке начертить гистограмму относительных частот и график плотности гипотетического распределения.
Построить график функции гипотетического распределения.
Варианты заданий
Вариант 1
59.49 44.71 51.50 37.23 40.32 49.31 27.52 45.73 40.97 49.26
62.47 44.35 50.89 55.05 44.90 67.64 51.06 44.25 45.68 56.50
51.64 51.13 56.53 34.69 59.04 48.13 36.27 42.86 45.09 47.30
36.44 53.07 44.85 45.05 49.97 62.43 34.29 37.52 34.40 41.45
48.60 66.47 38.80 49.02 58.96 52.63 49.23 54.76 64.32 39.98
45.32 45.54 53.35 44.08 41.45 63.07 53.35 36.52 52.49 54.88
46.71 41.44 46.70 46.53 48.91 45.91 48.24 60.20 49.00 60.78
38.50 61.58 54.53 60.94 41.62 33.84 44.05 33.88 64.14 37.44
Вариант 2
20.58 20.75 17.88 20.66 17.62 16.56 16.82 19.75 17.13 20.62
16.65 17.22 20.49 17.08 21.18 22.42 20.54 17.30 21.02 17.34
18.58 19.10 21.89 19.41 18.03 22.21 20.35 17.42 21.63 20.58
22.27 21.74 21.93 19.79 17.00 16.90 20.23 17.84 18.14 18.96
20.45 21.82 17.90 20.13 16.92 18.43 20.17 20.68 21.23 19.90
22.41 21.36 20.40 17.84 16.85 21.81 17.75 21.68 17.30 21.88
21.45 21.94 21.61 19.05 22.18 18.60 21.72 16.65 17.66 19.79
19.85 18.48 18.04 20.56 18.45 20.92 19.62 21.51 18.73 18.44
Вариант 3
0.75 8.16 1.36 2.23 0.79 1.92 1.48 0.47 3.97 0.15
0.99 0.41 0.32 5.74 0.80 0.31 2.43 2.92 4.20 1.16
1.61 1.09 4.82 2.62 0.40 0.30 6.35 4.05 2.16 0.47
0.10 2.94 0.52 2.43 6.68 0.93 0.29 0.37 5.67 0.62
Окончание варианта 3
1.42 2.93 0.98 1.51 0.15 0.74 3.86 5.79 1.24 0.44
0.86 4.88 1.38 3.37 1.54 13.12 0.13 0.85 2.00 2.29
0.56 0.87 0.15 0.75 2.52 3.36 0.96 3.06 2.37 6.85
1.61 4.60 0.49 1.07 3.68 0.19 2.24 2.26 4.09 4.52
Вариант 4
29.59 41.56 15.58 20.88 35.92 33.87 26.35 23.78 27.54 34.38
27.37 28.57 28.40 42.76 34.04 30.45 29.42 32.16 29.76 21.22
36.26 46.18 27.71 37.80 28.06 33.01 42.07 23.27 31.30 34.72
23.27 35.75 26.52 32.33 22.59 19.85 23.27 40.53 48.40 35.06
19.85 34.21 37.97 33.01 25.83 32.67 38.48 20.88 42.24 39.85
29.76 40.19 33.53 46.52 33.53 51.65 33.70 26.69 37.80 48.91
22.07 34.21 39.51 48.74 21.90 49.76 17.29 16.60 27.03 27.20
47.20 38.31 18.65 18.31 45.66 35.75 31.82 23.10 19.51 28.06
Вариант 5
19.10 27.96 8.93 44.36 25.63 19.95 5.35 6.82 9.85 20.91
21.24 45.21 23.83 36.70 35.18 38.26 39.93 23.85 23.41 47.41
14.29 7.20 45.97 12.51 34.97 35.19 5.99 15.12 27.35 40.19
10.66 14.59 8.76 5.71 36.33 40.26 35.99 25.36 42.86 37.96
14.65 34.17 24.82 41.56 5.99 20.49 48.01 9.70 42.08 41.85
28.64 11.15 8.90 34.71 12.57 16.38 38.83 36.32 30.71 29.35
29.48 35.01 10.96 40.59 47.76 9.78 9.90 42.13 11.81 48.90
10.96 12.81 20.37 42.65 31.21 26.20 16.84 36.41 17.73 27.81
Вариант 6
12.37 16.64 6.85 44.26 4.37 5.64 8.55 5.88 36.01 4.28
4.35 0.54 8.89 19.00 4.30 8.54 8.39 4.83 3.18 0.51
14.96 1.38 9.94 12.78 3.18 31.18 39.60 18.80 17.80 21.13
8.18 15.64 7.00 9.19 3.94 1.82 33.20 1.15 3.55 17.79
5.80 6.57 0.85 14.22 5.46 13.89 11.03 18.11 12.19 27.9
44.60 1.19 5.57 20.87 23.52 4.97 1.95 4.98 5.54 2.56
18.80 4.81 30.51 11.35 4.46 7.19 1.06 14.86 10.41 4.72
1.07 9.33 7.33 10.91 23.71 2.37 2.07 40.38 19.48 16.56
Вариант 7
43.33 44.87 48.13 39.96 43.71 41.02 47.27 33.42 49.19 40.83
49.58 41.79 39.29 40.54 46.88 41.21 41.40 41.60 43.04 41.12
38.52 53.23 43.90 47.65 42.94 38.81 49.38 43.04 36.69 46.69
48.90 46.69 38.13 49.96 48.04 38.71 48.23 44.10 43.23 45.63
Окончание варианта 7
39.58 49.87 46.40 46.69 41.60 48.33 36.98 51.79 47.46 38.23
40.25 42.94 37.65 39.48 50.44 39.67 39.96 43.81 41.02 39.58
49.87 39.87 40.15 39.10 29.96 47.27 46.12 37.08 40.35 43.52
39.48 35.83 48.90 43.52 43.13 41.21 39.48 43.33 48.42 46.50
Вариант 8
8.35 8.07 9.33 9.93 8.88 8.26 8.81 8.59 9.18 9.63
8.12 9.77 8.15 8.05 8.54 9.90 8.59 8.90 8.77 8.71
9.31 9.34 8.60 9.33 8.64 8.40 9.76 9.42 9.27 8.45
8.97 9.04 9.68 8.71 9.65 9.19 8.76 8.18 9.96 9.41
9.15 8.60 8.41 9.40 8.79 9.80 9.40 9.26 9.96 8.93
8.97 9.38 8.02 8.32 8.31 8.57 8.05 9.33 9.51 8.96
8.40 9.80 9.60 8.93 8.78 8.65 8.33 9.40 9.48 9.01
9.71 8.95 8.29 8.94 8.07 8.82 9.77 9.45 9.47 8.82
Вариант 9
2.94 8.82 4.54 4.45 0.24 9.59 3.12 5.73 0.82 18.07
0.94 1.04 3.68 0.28 0.99 2.40 1.91 5.41 3.62 2.26
2.79 18.16 8.91 8.83 10.05 0.36 5.78 12.87 5.19 2.72
1.58 0.59 2.63 8.86 1.29 0.28 16.93 5.37 27.91 5.26
0.59 3.93 1.96 0.74 0.10 1.41 1.39 2.86 2.54 17.97
0.60 4.90 7.89 4.08 3.28 0.09 3.51 2.92 1.90 2.63
2.25 23.70 6.46 6.57 1.43 3.82 3.01 8.88 6.71 14.32
1.14 1.69 1.57 1.65 1.71 0.37 0.23 7.80 3.76 9.17
Вариант 10
50.84 53.77 52.60 49.52 44.83 44.17 50.33 55.16 49.52 43.22
55.38 50.03 50.11 53.11 53.70 51.06 57.07 56.99 44.91 49.60
54.36 45.35 55.46 47.76 47.54 48.35 52.75 52.45 49.82 48.57
49.60 50.77 51.35 50.25 50.77 46.59 42.42 54.43 49.30 51.94
51.13 48.94 45.86 48.13 49.08 46.88 46.23 46.52 53.84 55.02
54.36 51.94 49.96 52.31 52.09 46.74 47.98 45.49 50.55 46.37
49.08 50.77 53.11 51.57 52.09 52.89 47.18 52.16 45.49 50.03
44.10 52.60 59.34 43.51 59.05 54.36 54.21 46.96 54.21 57.21
Вариант 11
39.02 30.67 41.19 19.48 42.66 16.06 22.30 39.78 33.10 44.59
24.39 36.46 44.16 16.30 21.41 20.77 12.00 19.24 29.93 24.67
39.89 37.85 26.06 36.88 38.01 20.48 31.73 20.61 40.34 14.32
32.84 38.45 21.26 17.58 35.91 21.67 32.28 35.48 30.35 29.68
12.89 42.58 20.92 25.67 18.62 13.24 33.78 36.50 41.24 29.77
Продолжение варианта 11
16.51 13.49 21.86 31.96 20.55 17.46 44.61 25.32 26.44 26.60
26.17 15.03 12.07 39.65 32.49 18.43 43.26 20.62 12.15 17.57
41.16 14.23 31.45 18.51 36.25 27.23 23.46 29.55 39.48 15.26
Вариант 12
3.36 5.72 0.61 17.42 4.26 2.37 6.52 2.21 4.13 5.42
5.08 0.64 3.62 0.04 7.79 1.99 11.24 9.92 4.01 12.68
3.02 12.58 2.43 10.88 3.76 0.39 3.32 0.79 0.86 7.47
7.94 3.80 14.81 1.42 9.78 0.16 1.78 1.67 2.28 4.48
2.39 1.76 4.85 0.35 0.63 0.01 8.17 6.92 1.13 0.47
3.71 15.15 5.52 3.80 1.33 2.77 2.64 3.22 0.45 1.64
5.57 8.31 10.88 1.96 3.04 3.59 0.42 4.02 2.72 7.36
0.07 12.95 3.41 5.03 11.55 0.56 5.55 13.96 0.96 3.86
Вариант 13
53.17 50.35 48.56 54.28 51.89 50.86 53.85 50.61 47.19 54.71
53.85 54.54 54.20 62.57 53.60 52.06 51.12 55.99 56.33 50.95
54.45 63.00 59.92 52.15 60.78 49.41 53.00 52.49 49.41 55.05
60.18 56.50 43.94 47.87 52.66 54.20 51.03 53.43 44.88 59.32
54.54 48.47 49.24 46.08 58.13 51.89 43.17 51.55 64.37 56.08
50.18 56.93 55.56 57.79 54.88 51.21 49.92 55.91 51.97 49.24
52.40 43.26 42.74 44.79 62.06 57.44 61.12 55.48 46.68 54.62
53.26 49.84 45.05 51.03 53.34 49.67 49.07 52.83 58.13 50.86
Вариант 14
31.13 21.77 23.16 35.45 55.91 19.26 35.02 61.93 37.42 41.60
37.63 42.16 53.98 49.35 37.83 32.16 48.60 24.92 53.01 52.32
14.86 52.40 34.49 29.86 49.83 45.84 20.62 37.34 49.11 38.12
27.60 41.49 36.03 42.23 53.97 16.34 54.85 51.86 42.84 30.11
60.02 59.78 62.97 20.12 57.41 21.20 62.28 23.63 15.95 48.07
39.26 63.20 39.80 42.31 35.34 63.88 52.99 57.21 17.50 21.05
47.96 29.16 39.17 25.05 14.49 24.92 48.57 32.40 37.59 18.43
55.15 52.84 27.79 14.07 27.26 28.12 56.51 37.41 23.32 24.77
Вариант 15
3.01 1.11 6.17 4.04 5.67 0.31 10.02 3.76 0.93 6.64
1.40 2.92 6.28 0.13 4.82 6.44 1.99 2.42 12.59 3.00
5.03 0.20 0.21 2.14 2.76 2.21 6.87 12.97 1.30 5.21
6.89 2.13 23.33 0.55 3.56 5.06 4.17 2.31 9.41 4.21
13.62 4.41 4.53 5.52 0.29 8.05 2.07 5.11 11.49 2.22
1.52 0.96 0.07 0.00 5.61 1.44 3.41 8.51 2.20 1.41
2.05 7.87 9.15 33.45 26.29 24.93 14.91 14.90 1.76 0.09
1.03 6.20 0.26 1.58 0.65 7.80 9.49 3.93 0.05 0.92
Вариант 16
42.92 46.72 44.64 45.19 41.29 48.81 39.12 42.20 49.26 51.43
57.22 48.99 39.30 40.75 44.10 49.44 48.35 47.09 38.22 49.17
42.29 47.18 49.17 51.52 44.01 49.98 37.58 48.53 43.38 49.80
40.48 42.02 55.23 44.91 46.72 42.20 47.63 45.46 40.66 46.27
44.19 44.64 48.53 48.71 49.44 49.71 48.53 45.73 43.56 47.81
39.67 42.83 49.35 53.06 52.15 51.97 41.20 43.29 38.85 46.27
45.00 44.19 46.36 49.35 55.14 48.53 53.51 47.63 48.99 40.03
39.76 43.65 52.33 42.83 46.00 40.75 44.64 44.01 47.09 46.81
Вариант 17
18.94 22.90 21.80 20.95 21.27 20.89 18.84 19.43 20.83 20.61
22.02 22.64 20.38 18.74 19.70 18.55 19.26 22.42 22.86 17.99
20.07 22.81 19.57 17.73 18.74 22.92 21.21 22.42 18.34 20.43
19.23 20.39 18.43 19.80 21.80 17.80 17.92 22.89 18.07 21.46
18.89 22.74 20.18 17.28 18.70 21.35 17.41 18.11 21.47 21.87
19.03 18.85 18.01 19.02 22.44 19.35 17.89 18.68 18.53 21.14
22.40 22.15 18.67 17.13 20.99 19.73 19.05 19.30 17.27 18.90
17.66 21.55 17.57 17.17 17.48 20.73 19.58 17.77 20.31 18.90
Вариант 18
5.64 6.27 0.36 0.11 0.07 1.67 7.66 10.03 3.82 1.63
4.83 8.28 17.19 5.43 0.38 6.60 0.80 0.72 2.12 0.70
0.28 0.23 7.16 5.13 3.49 0.53 4.27 4.27 0.84 7.02
0.40 12.36 3.35 0.89 0.58 8.08 0.53 1.28 6.88 4.15
0.16 9.92 0.16 5.57 4.53 0.15 1.56 0.02 0.16 0.10
0.70 0.80 2.47 4.61 2.45 3.60 2.09 0.57 1.97 0.23
2.61 1.00 4.09 4.37 0.76 1.73 3.58 4.77 1.80 1.16
3.36 1.72 1.35 4.99 0.24 1.35 0.26 1.42 0.01 4.02
Вариант 19
42.38 54.31 59.12 43.54 41.04 43.73 51.42 40.65 59.31 56.23
56.62 50.65 36.23 51.62 54.12 33.54 42.19 39.50 36.62 43.35
60.27 62.38 63.73 44.12 47.19 51.62 49.12 33.73 48.54 55.27
59.88 50.46 50.08 31.04 37.00 64.31 55.85 61.42 62.38 52.00
41.23 64.12 40.27 46.62 49.88 52.77 49.31 39.12 54.50 63.73
59.88 50.46 46.62 49.69 43.73 34.69 49.50 49.50 71.04 61.62
55.85 59.31 40.65 35.08 46.81 68.92 36.23 65.27 41.62 48.54
42.38 40.08 40.65 44.50 51.62 37.58 32.96 57.19 43.35 55.65
Вариант 20
74.76 67.59 34.98 28.64 72.73 52.53 55.70 31.43 50.44 37.40
40.52 58.53 44.70 38.51 53.21 49.43 29.03 29.89 47.50 71.11
20.76 31.87 54.71 58.33 33.73 32.45 68.85 76.09 57.78 61.84
21.65 51.77 25.72 50.99 46.68 71.28 36.91 62.92 20.43 34.68
22.80 56.38 65.31 77.37 35.59 70.70 73.41 77.88 39.03 54.03
56.09 54.40 68.43 21.89 72.87 36.57 39.98 56.84 35.27 61.65
66.70 34.65 65.85 31.59 29.04 53.53 31.06 32.23 70.33 35.02
51.16 49.33 36.41 66.17 74.09 55.24 29.52 57.86 39.72 23.15
Вариант 21
53.27 34.70 37.77 5.10 33.77 5.64 6.05 11.26 11.48 47.20
58.03 6.00 63.98 2.39 15.29 14.38 6.95 16.72 8.82 5.67
16.26 13.09 56.84 15.35 5.78 28.74 48.66 5.23 7.49 0.87
10.47 3.36 13.10 12.47 3.95 0.23 3.29 35.14 14.15 10.99
6.28 1.08 37.02 36.74 36.36 40.33 14.00 17.66 2.20 10.61
17.08 8.15 11.29 1.27 41.70 53.15 5.97 5.31 10.67 30.57
2.12 17.19 11.48 37.95 5.80 12.54 20.49 25.39 60.58 7.94
3.40 31.94 14.68 3.61 7.74 2.92 50.22 7.62 3.89 71.44
Вариант 22
53.70 43.70 57.43 46.77 50.51 51.17 56.77 58.64 47.43 54.03
51.72 49.52 46.45 41.72 45.90 40.40 51.06 55.24 49.96 46.77
58.75 50.51 57.65 47.43 46.12 49.96 51.06 56.88 52.16 51.17
47.21 51.17 50.62 48.75 51.28 50.18 57.43 54.91 48.86 50.51
55.57 49.63 52.82 55.79 43.37 63.04 47.21 55.46 51.17 59.85
53.59 41.94 58.53 68.64 52.71 52.71 53.92 66.55 40.51 52.49
39.74 55.46 57.10 54.91 51.94 41.17 53.48 34.80 48.86 49.30
41.39 54.25 51.83 50.84 49.41 51.39 46.77 50.73 56.23 47.32
Вариант 23
31.01 23.07 32.21 26.94 45.89 32.76 39.60 45.05 40.51 42.99
35.47 49.75 38.15 42.42 51.41 43.77 36.38 38.37 36.83 37.36
33.36 39.78 36.41 44.99 51.91 45.72 37.73 32.26 38.40 44.39
26.50 51.46 43.67 48.29 44.70 47.14 24.04 54.23 49.36 49.87
47.09 52.24 39.21 51.55 39.59 28.45 33.09 47.47 41.33 37.35
41.10 41.61 25.33 54.32 52.62 52.16 52.42 40.84 43.91 45.78
49.94 43.35 25.68 32.14 32.22 45.41 35.98 41.01 50.08 36.47
43.72 31.84 29.33 32.34 26.73 41.73 39.59 28.10 47.41 36.80
Вариант 24
2.17 1.34 0.68 3.11 1.55 6.98 0.25 3.49 8.66 4.09
7.82 15.50 4.92 6.78 2.56 2.74 4.82 3.44 5.30 0.73
0.33 12.02 1.17 9.85 6.69 4.52 13.17 0.28 2.01 1.64
4.68 0.62 8.80 3.98 4.87 1.74 2.96 0.95 15.33 0.75
6.53 18.95 7.01 12.77 0.04 1.25 9.39 6.78 0.62 2.09
1.35 9.44 3.96 1.35 13.10 0.80 0.25 7.22 4.47 10.78
2.19 0.66 7.44 2.93 2.18 2.03 13.35 8.43 4.83 8.40
0.07 3.71 10.00 8.44 6.15 0.55 1.25 2.24 7.30 0.63
Вариант 25
72.08 72.35 71.21 69.99 71.45 69.43 67.19 67.23 70.26 71.76
71.76 70.46 70.93 66.91 66.75 69.63 72.12 69.99 68.76 67.54
70.11 72.67 69.04 71.05 67.50 73.81 73.18 69.91 71.84 68.41
72.63 68.41 72.16 73.10 71.80 70.26 72.31 67.58 72.47 71.09
68.61 69.00 70.07 69.08 69.83 74.17 69.59 69.12 68.41 68.21
72.55 70.58 68.61 71.29 66.48 68.29 70.38 70.03 74.80 70.34
67.38 71.37 68.29 68.80 66.59 68.25 72.00 69.20 69.91 69.63
69.91 72.63 69.67 70.03 69.71 68.17 70.14 73.06 70.74 71.13
Вариант 26
27.36 26.08 26.03 29.88 26.07 28.93 27.68 36.61 30.24 28.39
33.66 38.91 28.74 28.70 36.02 30.18 34.14 29.26 31.48 39.24
36.27 26.54 27.15 28.18 28.40 30.64 35.34 34.40 38.92 39.97
38.18 32.22 32.99 33.37 36.61 28.82 39.17 32.28 31.98 38.27
34.64 28.73 36.46 30.23 35.51 37.52 28.79 29.33 38.37 38.39
28.79 26.30 32.19 28.85 33.36 31.49 26.51 32.30 32.72 36.31
37.59 30.74 29.29 35.58 35.94 34.57 36.67 36.86 29.38 31.78
35.58 35.05 35.91 32.02 38.85 31.36 28.60 31.04 33.77 30.71
Вариант 27
2.89 24.30 10.85 33.62 7.66 14.12 10.03 12.03 8.70 47.96
18.32 27.45 25.92 0.11 1.72 21.86 28.08 16.86 32.68 17.75
17.30 21.58 6.54 1.67 0.04 6.95 0.05 2.00 7.11 18.04
0.97 16.09 1.31 0.96 26.77 2.35 39.94 5.63 43.95 0.68
13.99 42.90 2.90 8.39 2.51 16.90 4.33 1.79 7.37 21.19
5.61 2.26 17.98 8.97 7.33 9.61 6.53 3.93 25.63 3.07
3.79 17.71 0.52 6.35 15.90 3.49 17.52 9.82 15.00 5.21
14.23 3.21 2.31 3.28 4.99 5.22 8.81 26.79 2.74 18.29
Вариант 28
73.65 72.25 72.25 72.00 71.71 73.06 71.71 73.65 72.29 74.53
74.97 73.54 74.45 74.23 71.78 72.84 68.74 72.99 72.18 70.61
74.42 73.76 75.73 70.50 74.64 73.46 75.40 75.26 75.51 72.66
76.25 72.36 72.44 75.44 68.70 73.35 74.60 75.59 75.00 72.29
75.81 71.19 71.56 73.83 69.80 75.48 73.10 74.20 71.85 77.82
73.10 72.36 74.89 72.62 70.57 74.71 72.99 74.09 75.59 73.79
74.01 71.89 74.78 73.65 72.88 77.60 72.91 74.53 75.77 75.00
74.23 76.83 73.17 74.60 70.86 72.36 73.50 74.93 75.11 68.81
Вариант 29
10.27 10.46 7.11 10.35 6.81 5.57 5.88 9.29 6.24 10.31
5.68 6.34 10.15 6.18 10.96 12.41 10.21 6.43 10.78 6.48
7.93 8.53 11.79 8.89 7.28 12.17 9.99 6.58 11.49 10.26
12.24 11.61 11.84 9.34 6.08 5.96 9.85 7.06 7.41 8.37
10.11 11.71 7.14 9.74 5.99 7.75 9.78 10.38 11.01 9.47
12.39 11.17 10.05 7.06 5.91 11.70 6.96 11.54 6.44 11.78
11.27 11.85 11.46 8.47 12.13 7.95 11.60 5.67 6.86 9.33
9.41 7.81 7.29 10.24 7.78 10.66 9.14 11.35 8.11 7.77
Вариант 30
2.53 1.35 5.00 1.17 0.11 0.10 0.14 2.08 3.62 0.18
1.50 5.84 2.16 0.83 0.61 3.23 6.38 3.32 3.07 2.76
0.95 0.18 1.33 5.11 1.83 4.56 3.94 3.33 0.30 18.65
0.69 2.10 0.32 5.95 6.97 1.00 0.22 1.27 9.38 2.92
1.39 4.94 3.39 7.84 9.06 6.84 0.35 1.16 1.06 5.13
5.98 3.81 0.61 1.14 1.52 0.73 1.03 0.58 19.34 6.98
1.66 1.32 6.47 7.60 1.53 3.83 2.48 1.82 11.56 17.17
6.70 9.28 5.40 2.82 4.87 1.24 1.43 0.26 6.03 3.26
Примеры выполнения работы
Проверка гипотезы о нормальном распределении
Загрузим пакет stats и подпакеты transform, describe.
> restart:with(stats):with(transform):with(describe):
Вводим реализацию выборки (см. данные своего варианта):
> Y:=[15.41,13.32,14.28,12.26,12.70,13.97,10.89,13.46,12.79,
13.96,15.83,13.27,14.19,14.78,13.35,16.56,14.22,13.26,13.46,
14.98,14.30,14.23,14.99,11.90,15.34,13.80,12.13,13.06,13.37,
13.69,12.15,14.50,13.34,13.37,14.06,15.82,11.85,12.30,11.86,
12.86,13.87,16.39,12.49,13.93,15.33,14.44,13.96,14.74,16.09,
12.65,13.40,13.44,14.54,13.23,12.86,15.91,14.54,12.16,14.42,
14.76,13.60,12.86,13.60,13.58,13.91,13.49,13.82,15.51,13.92,
15.59,12.44,15.70,14.71,15.61,12.88,11.79,13.23,11.79,16.06,
12.29];

![]()
Определим объём выборки (подсчитаем количество значений в выборке) и рассчитаем количество интервалов разбиения k:
> n:=count(Y);k:=round(1+1.4*ln(n));
![]()
![]()
Проведём сортировку выборки (варианты расположим в порядке возрастания):
> Y1:=statsort(Y);

![]()
Находим минимальное и максимальное значения выборки и длину интервала разбиения:
> ymin:=Y1[1];ymax:=Y1[n];h:=(ymax-ymin)/k;
![]()
![]()
![]()
Вычислим границы интервалов разбиения:
> Y2:=[seq(ymin+(i-1)*(h+0.0001)..ymin+i*(h+0.0001),i=1..k)];

Находим вектор точек разбиения:
> Z:=[seq(ymin+(i-1)*(h+0.0001),i=1..k+1)];
![]()
Составляем интервальный ряд частот Y3 (каждому интервалу поставим в соответствие частоту ni, т.е. число элементов выборки, попадающих в данный интервал) и вектор частот Y3f:
> Y3:=statsort(transform[tallyinto](Y1,Y2));

> Y3f:=transform[frequency](Y3);
![]()
Получим интервальный ряд относительных частот (каждому интервалу поставим в соответствие относительную частоту, т.е. частоту, делённую на объём выборки):
> Y4:=transform[scaleweight[1/n]](Y3);
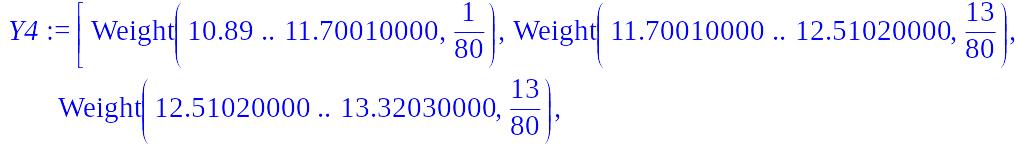


Строим гистограмму относительных частот:
> Hist:=statplots[histogram](Y4,color=green):
> plots[display](Hist);
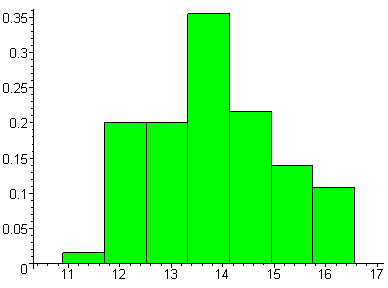
По виду гистограммы выдвигаем гипотезу о нормальном распределении генеральной совокупности.
Находим накопленные частоты Y5 (накопленная частота показывает, сколько наблюдалось значений, меньших заданного x) и относительные накопленные частоты Y6:
> Y5:=transform[cumulativefrequency](Y3);
![]()
> Y6:=transform[cumulativefrequency](Y4);
![]() .
.
Строим график эмпирической функции распределения:
> p:=[seq(plot(Y6[i],Y2[i],color=blue),i=1..k)]:plots[display](p);
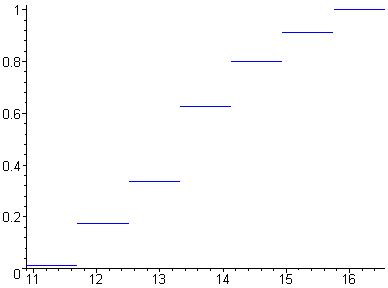
Находим точечные оценки математического ожидания a (выборочное среднее значение), дисперсии S и среднего квадратического отклонения s:
> a:=mean(Y);
![]()
> S:=variance(Y);
![]()
> s:=standarddeviation(Y1);
![]() .
.
Находим исправленные оценки дисперсии (несмещённая оценка дисперсии) и среднего квадратического отклонения:
> S1:=S*n/(n-1);
![]()
> s1:=sqrt(S1);
![]() .
.
Вычислим вероятности попадания значения случайной величины в первый и последний (k-ый) интервалы:
> p[1]:=evalf(1/(sqrt(2*Pi)*s1)*int(exp(-(t-a)^2/(2*S1)),t=-infinity..Z[2]));
![]() .
.
> p[k]:=evalf(1/(sqrt(2*Pi)*s1)*int(exp(-(t-a)^2/(2*S1)),t=Z[k]..infinity));
![]() .
.
Вычислим вероятности
попадания значения случайной величины
во 2, 3, …, k
-1 интервалы по формулам
 ,
где
,
где
![]() :
:
> for i from 2 to k-1 do p[i]:=evalf(1/(sqrt(2*Pi)*s1)*int(exp(-(t-a)^2/(2*S1)),t=Z[i]..Z[i+1])) od;
![]()
![]()
![]()
![]()
![]()
Находим теоретические частоты npi:
> for i from 1 to k do n*p[i] od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Так как на первом и последнем интервалах npi < 5, то объединим 1-й со 2-м и 6-й с 7-м интервалы и пересчитаем соответствующие вероятности и частоты:
> p[2]:=p[1]+p[2]; Y3f[2]:=Y3f[1]+Y3f[2]; p[6]:=p[6]+p[7]; Y3f[6]:= Y3f[6] +Y3f[7];
![]()
![]()
![]()
![]() .
.
Сравним эмпирические
ni
и теоретические npi
частоты, для этого находим наблюдаемое
значение по формуле
![]() ,
где i
= 2,3,…,6, так
как два первых и два последних интервала
объединили.
,
где i
= 2,3,…,6, так
как два первых и два последних интервала
объединили.
> chi2:=sum((Y3f[j]-n*p[j])^2/(n*p[j]),j=2..6);
![]() .
.
По таблице
критических точек распределения
,
по заданному
уровню
значимости
и числу
степеней свободы ν
= s-l-1
(s
– число
интервалов после пересчёта, l
– число параметров в гипотетической
функции распределения) находят критическую
точку
![]() .
В нашем случае
= 0,01(см. задание), s
= 5, l
= 2, т.е. ν
= 5-2-1=2, тогда
.
В нашем случае
= 0,01(см. задание), s
= 5, l
= 2, т.е. ν
= 5-2-1=2, тогда
![]() .
.
Так как
![]() ,
то гипотеза о нормальном распределении
генеральной совокупности принимается.
,
то гипотеза о нормальном распределении
генеральной совокупности принимается.
Запишем гипотетическую
функцию плотности распределения
 и построим на одном рисунке гистограмму
относительных частот и график плотности
гипотетического распределения.
и построим на одном рисунке гистограмму
относительных частот и график плотности
гипотетического распределения.
> f:=evalf(1/(sqrt(2*Pi)*s1)*exp(-(x-a)^2/(2*S1)));
![]()
> f1:=plot(f,x=ymin-2..ymax+2):
> plots[display](Hist,f1);
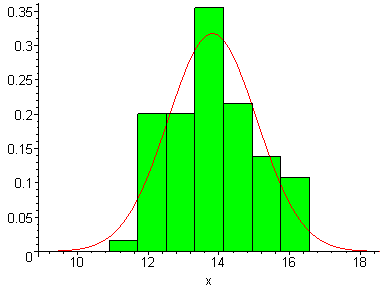
Запишем гипотетическую
функцию распределения
 и построим её график.
и построим её график.
> F:=evalf(1/(sqrt(2*Pi)*s1))*Int(exp(-(t-a)^2/(2*S1)),t=-infinity..x);
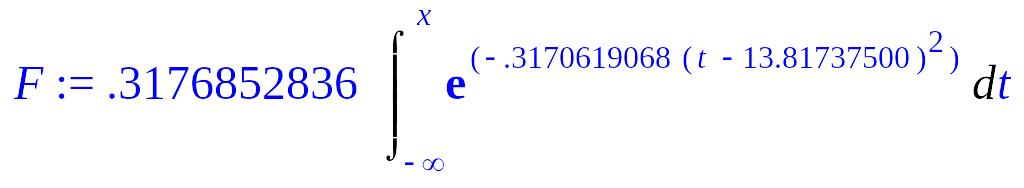
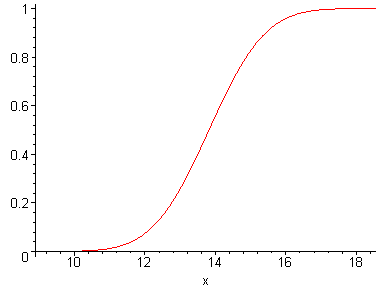
> F1:=plot(F,x=ymin-2..ymax+2):
> plots[display](F1);
Проверка гипотезы о равномерном распределении
Загрузим пакет stats и подпакеты transform, describe.
> restart:with(stats):with(transform):with(describe):
Вводим реализацию выборки (см. данные своего варианта):
> Y:=[10.63,26.04,6.09,23.42,5.25,24.87,3.24,6.24,4.96,13.74,
13.25,21.71,20.96,34.72,8.71,9.06,19.12,20.02,8.58,34.52,
14.29,32.13,13.40,26.62,20.13,6.48,30.30,9.16,12.39,21.48,
5.28,13.82,21.77,32.26,21.70,7.87,29.74,21.11,17.79,17.67,
27.76,27.34,5.87,5.02,12.32,25.43,31.07,24.85,15.14,25.85,
7.14,12.78,24.99,27.51,22.59,29.00,34.62,17.65,9.02,21.51,
11.24,22.13,10.48,13.20,12.34,25.25,31.73,28.72,14.11,9.62,
17.54,12.87,27.15,18.08,19.94,29.86,30.53,10.30,33.13,23.41];

![]()
Определим объём выборки (подсчитаем количество значений в выборке) и рассчитаем количество интервалов разбиения k:
> n:=count(Y);k:=round(1+1.4*ln(n));
Проведём сортировку выборки (варианты расположим в порядке возрастания):
> Y1:=statsort(Y);

![]()
Находим минимальное и максимальное значения выборки и дли-ну интервала разбиения:
> ymin:=Y1[1];ymax:=Y1[n];h:=(ymax-ymin)/k;
![]()
![]()
![]()
Вычислим границы интервалов разбиения:
> Y2:=[seq(ymin+(i-1)*(h+0.0001)..ymin+i*(h+0.0001),i=1..k)];

Находим вектор точек разбиения:
> Z:=[seq(ymin+(i-1)*(h+0.0001),i=1..k+1)];
![]()
Составляем интервальный ряд частот Y3 (каждому интервалу поставим в соответствие частоту ni, т.е. число элементов выборки, попадающих в данный интервал) и вектор частот Y3f:
> Y3:=statsort(transform[tallyinto](Y1,Y2));

![]()
> Y3f:=transform[frequency](Y3);
![]()
Получим интервальный ряд относительных частот (каждому интервалу поставим в соответствие относительную частоту, т.е. частоту, делённую на объём выборки):
> Y4:=transform[scaleweight[1/n]](Y3);
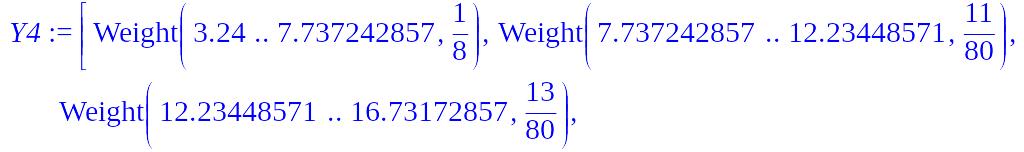


Строим гистограмму относительных частот:
> Hist:=statplots[histogram](Y4,color=green):
> plots[display](Hist);
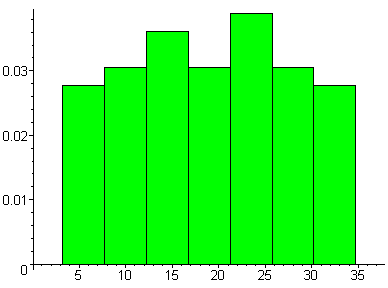
По виду гистограммы выдвигаем гипотезу о равномерном распределении генеральной совокупности.
Находим накопленные частоты Y5 (накопленная частота показывает, сколько наблюдалось значений, меньших заданного x) и относительные накопленные частоты Y6:
>Y5:=transform[cumulativefrequency](Y3);
![]()
>Y6:=transform[cumulativefrequency](Y4);
![]()
Строим график эмпирической функции распределения:
> p:=[seq(plot(Y6[i],Y2[i],color=blue),i=1..k)]:plots[display](p);
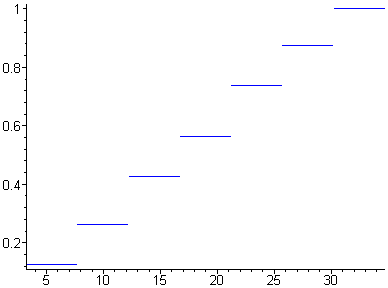
Находим точечные оценки математического ожидания m (выборочное среднее значение), дисперсии S и среднего квадратического отклонения s:
> m:=mean(Y);
![]()
> S:=variance(Y);
![]()
> s:=standarddeviation(Y1);
![]()
Находим исправленные оценки дисперсии (несмещённая оценка дисперсии) и среднего квадратического отклонения:
> S1:=S*n/(n-1);
![]()
> s1:=sqrt(S1);
![]()
Находим
точечные оценки параметров равномерного
распределения:
![]() ,
где
,
где
![]()
> a:= m-sqrt(3.0)*s1; b:= m+sqrt(3.0)*s1;
![]()
![]()
Вычислим вероятности попадания значения случайной величины в первый и последний (k-ый) интервалы:
> p[1]:=(Z[2]-a)/(b-a);
![]()
> p[k]:=(b-Z[k])/(b-a);
![]()
Вычислим
вероятности попадания значения случайной
величины во 2, 3, …, k-1
интервалы по формулам
![]() :
:
> for j from 2 to 6 do p[j]:=(Z[j+1]-Z[j])/(b-a) od;
![]()
![]()
![]()
![]()
![]()
Находим теоретические частоты npi:
> for j from 1 to k do n*p[j] od;
![]()
![]()
![]()
![]()
![]()
Так как все npi > 5, то пересчёт не делаем, число интервалов остаётся прежним: k = 7.
Сравним
эмпирические ni
и теоретические npi
частоты, для этого находим наблюдаемое
значение по формуле
![]() .
.
> chi2:=sum((Y3f[i]-n*p[i])^2/(n*p[i]),i=1..7);
![]()
По таблице
критических точек распределения
,
по заданному
уровню
значимости
и числу
степеней свободы ν = s-l-1
(s
– число
интервалов после пересчёта, l
– число параметров в гипотетической
функции распределения) находят критическую
точку
.
В нашем случае
= 0,01(см. задание),
s
= k
= 7, l
= 2, т.е. ν = 7-2-1=4, тогда
![]() .
.
Так как , то гипотеза о равномерном распределении генеральной совокупности принимается.
Запишем гипотетическую
функцию плотности распределения
![]()
и построим на одном рисунке гистограмму относительных частот и график плотности гипотетического распределения.
> f:=piecewise(x<a,0,x>=a and x<=b,1/(b-a),x>b,0);

> f1:=plot(f,x=ymin-1..ymax+1):
> plots[display](Hist,f1);
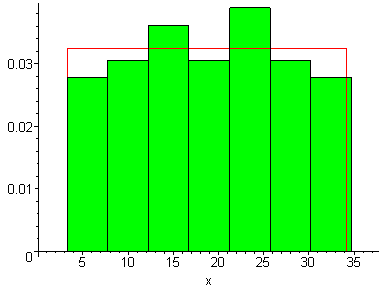
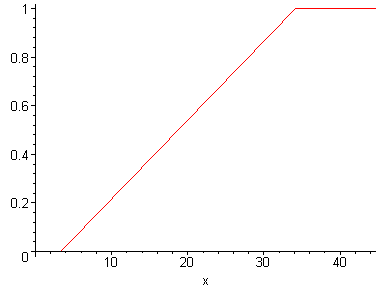
Запишем гипотетическую функцию распределения
![]()
и построим её график.
> F:=piecewise(x<a,0,x>=a and x<=b,(x-a)/(b-a),x>b,1);

> F1:=plot(F,x=0..ymax+10):
> plots[display](F1);
Проверка гипотезы о показательном распределении
Загрузим пакет stats и подпакеты transform, describe.
> restart:with(stats):with(transform):with(describe):
Вводим реализацию выборки (см. данные своего варианта):
> Y:=[0.63,16.04,6.09,3.42,9.25,2.87,1.34,11.24,4.96,3.74,
9.25,1.71,20.96,6.72,8.71,1.06,19.12,0.02,8.58,31.52,
0.29,8.13,17.40,1.62,3.13,18.48,30.30,9.16,2.39,1.48,
5.28,13.82,1.77,2.26,1.70,7.87,9.74,21.21,7.79,.67,
18.76,8.34,1.87,7.02,2.32,2.43,3.07,4.85,5.14,5.85,
1.14,2.78,4.99,7.51,2.59,2.00,11.62,1.65,9.02,1.51,
11.21,22.13,0.48,13.20,12.34,5.25,5.73,0.72,14.11,9.62,
13.54,12.87,27.11,1.08,5.94,1.86,30.53,6.30,20.13,3.41];

![]()
Определим объём выборки (подсчитаем количество значений в выборке) и рассчитаем количество интервалов разбиения k:
> n:=count(Y);k:=round(1+1.4*ln(n));
Проведём сортировку выборки (варианты расположим в порядке возрастания):
> Y1:=statsort(Y);

![]()
Находим минимальное и максимальное значения выборки и длину интервала разбиения:
> ymin:=Y1[1];ymax:=Y1[n];h:=(ymax-ymin)/k;
![]()
![]()
![]()
Вычислим границы интервалов разбиения:
> Y2:=[seq(ymin+(i-1)*(h+0.0001)..ymin+i*(h+0.0001),i=1..k)];

Находим вектор точек разбиения:
> Z:=[seq(ymin+(i-1)*(h+0.0001),i=1..k+1)];
![]()
Составляем интервальный ряд частот Y3 (каждому интервалу поставим в соответствие частоту ni, т.е. число элементов выборки, попадающих в данный интервал) и вектор частот Y3f:
> Y3:=statsort(transform[tallyinto](Y1,Y2));

> Y3f:=transform[frequency](Y3);
![]()
Получим интервальный ряд относительных частот (каждому интервалу поставим в соответствие относительную частоту, т.е. частоту, делённую на объём выборки):
> Y4:=transform[scaleweight[1/n]](Y3);
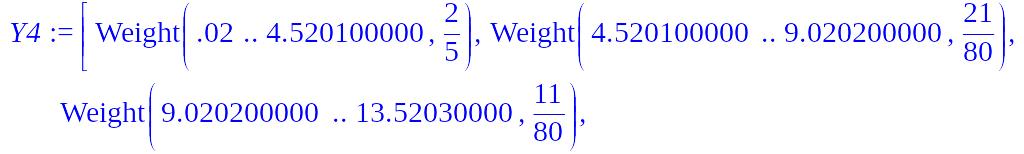
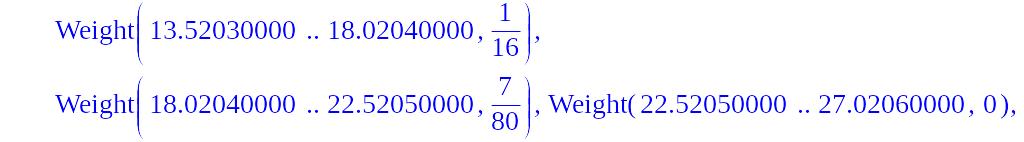
![]()
Строим гистограмму относительных частот:
> Hist:=statplots[histogram](Y4,color=green):
> plots[display](Hist);
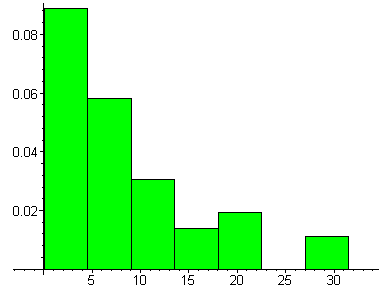
По виду гистограммы выдвигаем гипотезу о показательном распределении генеральной совокупности.
Находим накопленные частоты Y5 (накопленная частота показывает, сколько наблюдалось значений, меньших заданного x) и относительные накопленные частоты Y6:
> Y5:=transform[cumulativefrequency](Y3);
![]()
> Y6:=transform[cumulativefrequency](Y4);
![]()
Строим график эмпирической функции распределения:
> p:=[seq(plot(Y6[i],Y2[i],color=blue),i=1..k)]:plots[display](p);
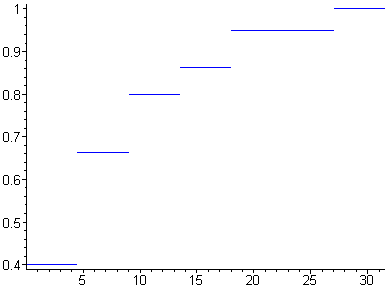
Находим точечные оценки математического ожидания a (выборочное среднее значение), дисперсии S и среднего квадратического отклонения s:
> a:=mean(Y);
![]()
> S:=variance(Y);
![]()
> s:=standarddeviation(Y1);
![]()
Находим исправленные оценки дисперсии (несмещённая оценка дисперсии) и среднего квадратического отклонения:
> S1:=S*n/(n-1);
![]()
> s1:=sqrt(S1);
![]()
Находим точечную оценку параметра показательного распределения:
> lambda:=1/a;
![]()
Вычислим вероятности попадания значения случайной величины в первый и последний (k-ый) интервалы:
> p[1]:=int(lambda*exp(-lambda*t),t=0..Z[2]);
p[k]:=int(lambda*exp(-lambda*t),t=Z[k]..infinity);
![]()
![]()
Вычислим вероятности
попадания значения случайной величины
во 2, 3, …, k
-1 интервалы по формулам
 :
:
> for j from 2 to k-1 do p[j]:=int(lambda*exp(-lambda*t),t=Z[j]..Z[j+1]) od;
![]()
![]()
![]()
![]()
![]()
Находим теоретические частоты npi:
> for j from 1 to k do n*p[j] od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Так как на трёх последних интервалах npi < 5, то объединим эти интервалы и пересчитаем соответствующие вероятности и частоты, при этом число интервалов будет 5:
> p[5]:= p[5]+p[6]+p[7];Y3f[5]:=Y3f[5]+Y3f[6]+Y3f[7];
![]()
![]()
Сравним эмпирические
ni
и теоретические npi
частоты, для этого находим наблюдаемое
значение по формуле
![]() ,
где i
= = 1,2,…,5, так
как три последних интервала объединили.
,
где i
= = 1,2,…,5, так
как три последних интервала объединили.
> chi2:=sum((Y3f[i]-n*p[i])^2/(n*p[i]),i=1..5);
![]()
По таблице
критических точек распределения
,
по заданному
уровню
значимости
и числу
степеней свободы ν = s-l-1
(s
– число
интервалов после пересчёта, l
– число параметров в гипотетической
функции распределения) находят критическую
точку
.
В нашем случае
= 0,01(см. задание), s
= 5, l
= 1, т.е. ν = 5-1-1=3, тогда
![]() .
.
Так как , то гипотеза о показательном распределении генеральной совокупности принимается.
Запишем гипотетическую
функцию плотности распределения
![]() и построим на одном рисунке гистограмму
относительных частот и график плотности
гипотетического распределения.
и построим на одном рисунке гистограмму
относительных частот и график плотности
гипотетического распределения.
> f:=piecewise(x<0,0,x>=0,evalf(lambda*exp(-lambda*x)));
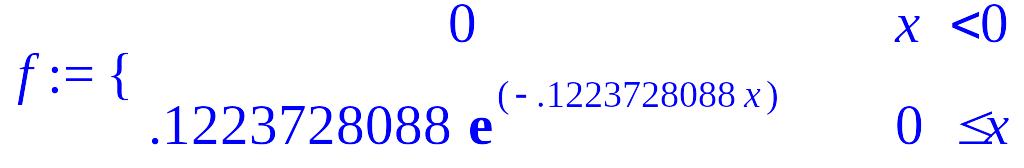
> f1:=plot(f,x=-10..ymax+10):
> plots[display](Hist,f1);
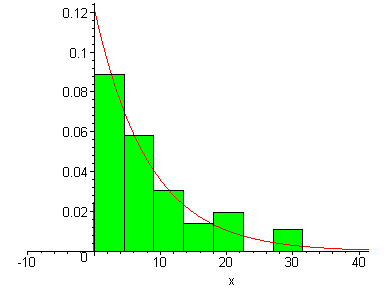
Запишем гипотетическую функцию распределения
![]()
и построим её график.
> F:=piecewise(x<0,0,x>=0,1-exp(-lambda*x));
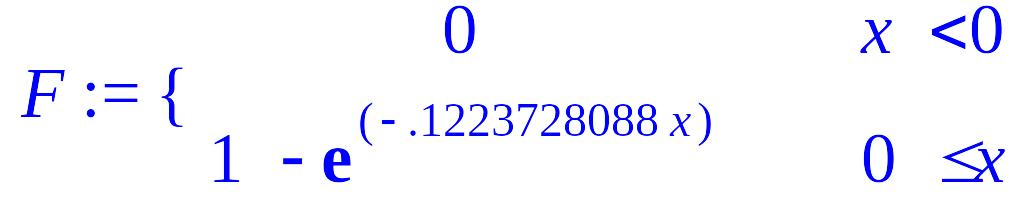
> F1:=plot(F,x=-10..ymax+10):
> plots[display](F1);