Контрольные вопросы
Какие испытания называются независимыми? Приведите при-меры независимых испытаний.
Что понимают под схемой Бернулли? Приведите примеры ситуаций, в которых присутствует схема Бернулли.
Что такое «успех» и «неудача» в схеме Бернулли? Как связаны их вероятности?
Запишите формулу Бернулли. Какую вероятность вычисляют по этой формуле? Приведите примеры задач, в которых используется формула Бернулли.
В каких случаях и какие приближённые формулы используют в схеме Бернулли ?
При каких условиях более точный результат даёт та или иная приближённая формула?
Приведите примеры задач, в которых используются формула Пуассона и локальная теорема Муавра – Лапласа.
Как найти вероятность того, что в п испытаниях схемы Бернулли «успех» наступит: а) не более m раз; б) более m раз; в) не менее m раз; г) менее m раз.
Сформулируйте интегральную теорему Муавра – Лапласа. Приведите примеры задач, в которых используется эта теорема.
Каким образом нужно решать следующую задачу: найти вероятность того, что в 450 независимых испытаниях «успех» наступит не менее 10 и не более 15 раз, если вероятность «успеха» в каждом испытании равна 0,3 (если вероятность «успеха» в каждом испытании равна 0,03).
Лабораторная работа 2 Исследование дискретной и непрерывной случайных величин
Цель работы: научиться использовать закон распределения случайной величины для нахождения вероятностей и числовых характеристик исследуемой случайной величины.
Краткий теоретический материал. Случайной величиной (с.в.) называется величина, которая в результате опыта со случайным исходом принимает то или иное значение. Случайная величина называется дискретной (д.с.в.), если множество её значений конечно или счётно. Случайная величина называется непрерывной, если множество её значений занимает некоторый промежуток.
Законом распределения с.в. называется правило, которое связывает значения с.в. и соответствующие им вероятности. Закон распределения д.с.в. можно задать с помощью ряда или функции распределения. Рядом распределения д.с.в. ξ называется таблица, в верхней строке которой перечислены все значения с.в., а в нижней – вероятности этих значений.
ξ |
х1 |
x2 |
… |
xn |
… |
P |
р1 |
р2 |
… |
pn |
… |
При этом
.
Функцией
распределения с.в. ξ
называется вероятность того, что она
примет значение меньше, чем заданное
x:
.
Закон распределения
непрерывной с.в. можно задать с помощью
плотности или функции распределения.
Плотностью
распределения
непрерывной с.в. называется первая
производная от функции распределения:
(предполагается,
что функция распределения дифференцируема
при всех действительных х
за исключением,
быть может, конечного числа точек).
Отметим некоторые свойства плотности и функции распределения.
Математическим
ожиданием
дискретной с.в. ξ называется её среднее
значение
(если множество значений с.в. счётно, то
рассматривается числовой ряд).
Математическим
ожиданием
непрерывной с.в. ξ называется её среднее
значение
.
Дисперсией
с.в. ξ называется среднее значение
квадрата отклонения с.в. от
её математического ожидания:
.
Для дискретной
с.в.
(если
множество значений с.в. счётно, то
рассматривается числовой ряд).
Для непрерывной
с.в.
.
Примеры распределений с.в.
1)
Пусть Х –
число успехов в схеме Бернулли (n
– число испытаний, p
– вероятность успеха, q=1–p).
Тогда закон распределения случайной
величины Х
задаётся соответствием
,
i=0,
…, n.
Этот закон называется биномиальным.
Для этого
распределения математическое ожидание
и дисперсия
,
.
2) Случайная величина Х называется равномерно распределённой на отрезке [a, b], если её плотность распределения имеет вид:
График плотности и функции распределения приведены на рисунке 1.
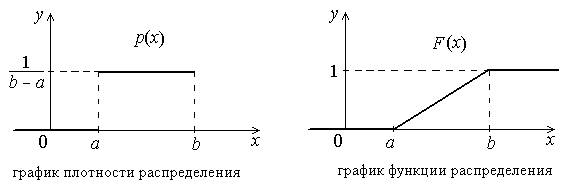
а)
б)
Рис. 1. График плотности и функции распределения:
а – график плотности распределения; б – график функции распределения
Для
равномерного распределения
,
.
Экспоненциальное (или показательное) распределение имеет пло-тность распределения вида:
Например, из практики известно, что время безотказной работы телевизора распределено по показательному закону. Смысл параметра в том, что число 1/ равно среднему времени безотказной работы телевизора.
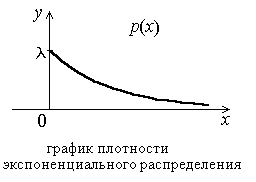
Рис. 2. График плотности экспоненциального распределения
Математическое
ожидание и дисперсия показательного
распределения, соответственно, равны:
,
.
Случайная величина Х называется нормально распределённой (имеющей распределение Гаусса), если её плотность вероятности имеет вид:
.
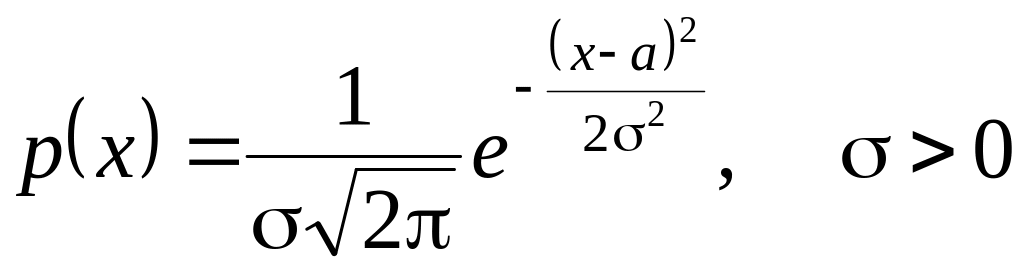Нормальное распределение будем обозначать N (a,). Тогда XN(a,) означает, что с.в. X имеет нормальное распределение с параметрами a, . Плотность зависит от двух параметров a и > 0. Если параметры a = 0, σ = 1, то такая нормально распределённая случайная величина называется стандартной нормальной случайной величиной.
Математическое
ожидание и дисперсия нормального
распределения, соответственно, равны:
,
.
Функция распределения равна:
.
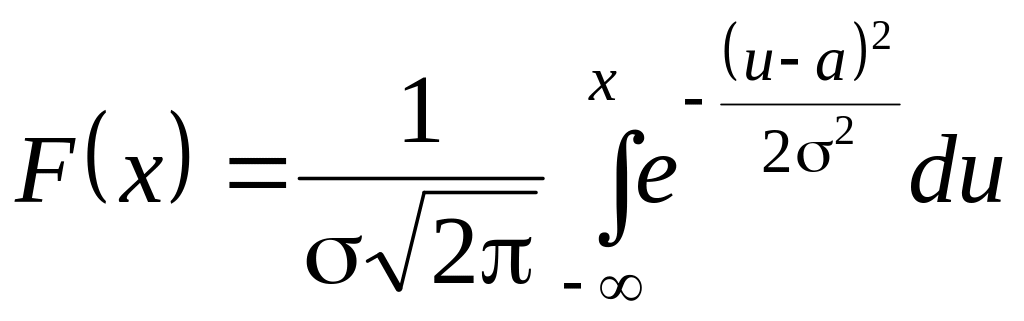График плотности нормального распределения изображён на рисунке 3.
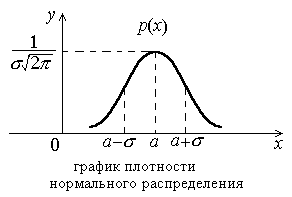
Рис. 3. График плотности нормального распределения
В природе часто встречаются нормально распределённые с.в. Так, «естественные» размеры человека (рост, вес и т.д.), деревьев (высота, диаметр ствола) распределены нормально.
Задание1. Для данной дискретной случайной величины построить многоугольник распределения, найти функцию распределения и построить её график. Найти математическое ожидание и дисперсию.
Варианты заданий
Вариант 1
X |
-5 |
2 |
4 |
7 |
13 |
P |
0,3 |
0,1 |
0,25 |
0,15 |
0,2 |
Вариант 2
X |
-4 |
-2 |
0 |
1 |
3 |
P |
0,2 |
0,25 |
0,2 |
0,15 |
0,2 |
Вариант 3
X |
-5 |
-2 |
0 |
7 |
8 |
P |
0,2 |
0,3 |
0,1 |
0,25 |
0,15 |
Вариант 4
X |
-7 |
-4 |
-2 |
0 |
3 |
P |
0,35 |
0,15 |
0,2 |
0,1 |
0,2 |
Вариант 5
X |
-6 |
-3 |
0 |
2 |
5 |
P |
0,25 |
0,2 |
0,1 |
0,2 |
0,25 |
Вариант 6
X |
0 |
2 |
4 |
7 |
8 |
P |
0,3 |
0,1 |
0,2 |
0,05 |
0,35 |
Вариант 7
X |
-5 |
-2 |
0 |
7 |
8 |
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 8
X |
-2 |
-1 |
4 |
5 |
7 |
P |
0,3 |
0,15 |
0,2 |
0,1 |
0,25 |
Вариант 9
X |
1 |
2 |
4 |
5 |
8 |
P |
0,3 |
0,3 |
0,15 |
0,05 |
0,2 |
Вариант 10
X |
-6 |
-5 |
-3 |
-2 |
0 |
P |
0,2 |
0,2 |
0,1 |
0,35 |
0,15 |
Вариант 11
X |
-3 |
-1 |
0 |
2 |
3 |
P |
0,1 |
0,2 |
0,15 |
0,05 |
0,5 |
Вариант 12
X |
-5 |
-4 |
-2 |
0 |
1 |
P |
0,4 |
0,2 |
0,1 |
0,1 |
0,2 |
Вариант 13
X |
-1 |
0 |
3 |
5 |
8 |
P |
0,3 |
0,15 |
0,2 |
0,05 |
0,3 |
Вариант 14
X |
-5 |
-3 |
0 |
3 |
9 |
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 15
X |
-4 |
0 |
2 |
3 |
5 |
P |
0,3 |
0,1 |
0,25 |
0,15 |
0,2 |
Вариант 16
X |
-2 |
-1 |
0 |
1 |
4 |
P |
0,2 |
0,25 |
0,2 |
0,15 |
0,2 |
Вариант 17
X |
-5 |
-1 |
0 |
4 |
5 |
P |
0,2 |
0,3 |
0,1 |
0,25 |
0,15 |
Вариант 18
X |
-8 |
-6 |
-4 |
-3 |
1 |
P |
0,35 |
0,15 |
0,2 |
0,1 |
0,2 |
Вариант 19
X |
-3 |
-2 |
0 |
2 |
3 |
P |
0,25 |
0,2 |
0,1 |
0,2 |
0,25 |
Вариант 20
X |
-1 |
2 |
4 |
5 |
9 |
P |
0,3 |
0,1 |
0,2 |
0,05 |
0,35 |
Вариант 21
X |
-3 |
-2 |
1 |
3 |
5 |
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 22
X |
-3 |
-1 |
1 |
2 |
6 |
P |
0,3 |
0,15 |
0,2 |
0,1 |
0,25 |
Вариант 23
X |
-11 |
-6 |
-2 |
0 |
2 |
P |
0,3 |
0,3 |
0,15 |
0,05 |
0,2 |
Вариант 24
X |
-1 |
0 |
1 |
4 |
10 |
P |
0,2 |
0,2 |
0,1 |
0,35 |
0,15 |
Вариант 25
X |
-3 |
-1 |
1 |
2 |
5 |
P |
0,1 |
0,2 |
0,15 |
0,05 |
0,5 |
Вариант 26
X |
-2 |
-1 |
0 |
2 |
4 |
P |
0,1 |
0,2 |
0,15 |
0,15 |
0,4 |
Вариант 27
X |
-2 |
-1 |
1 |
3 |
6 |
P |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
Вариант 28
X |
-3 |
-1 |
1 |
2 |
5 |
P |
0,3 |
0,1 |
0,1 |
0,3 |
0,2 |
Вариант 29
X |
-4 |
-1 |
1 |
3 |
5 |
P |
0,2 |
0,1 |
0,15 |
0,15 |
0,4 |
Вариант 30
X |
-2 |
0 |
1 |
2 |
4 |
P |
0,3 |
0,1 |
0,2 |
0,1 |
0,3 |