О писание эксперимента

Экспериментальная часть этой работы включает два опыта. В первом исследуется плоский конденсатор с различными диэлектриками. Схема эксперимента изображена на Рис.3.

Конденсатор С – разборный, С₀ смонтирован в том же модуле и имеет емкость 10.2нФ. В качестве вольтметров V₁ и V₂ используется GDM‑8135, подключенный либо к съемной пластине, либо к точке соединения конденсаторов.

Генератор GFG-8216A выдает синусоидальный сигнал с частотой 2-3кГц.

Конденсаторы С и С₀ образуют емкостной делитель напряжения. Зная выходное напряжение генератора U и напряжение U₀ на эталонном конденсаторе С₀, емкость разборного конденсатора С находят по формуле:

(6)

Найдя емкость конденсатора с воздушным зазором С_В, емкость конденсатора с диэлектриком С и считая диэлектрическую проницаемость воздуха за единицу, можно определить диэлектрическую проницаемость ε различных веществ из соотношения:

(7)

где d₀ = 2мм – толщина воздушного зазора, d – толщина диэлектрика.

Порядок выполнения работы

1. Согласно описанию эксперимента и рисунку собрать схему.

2. После проверки собранной схемы преподавателем, включить питание приборов. Меняя напряжение U от 3В до максимального значения, троекратно измерить U и U₀.

3. Установить выходное напряжение генератора 5–6В. Для различных диэлектриков (стекло, оргстекло, текстолит) измерить напряжения U₀. Толщина диэлектрика указана на образцах.

4. По формуле плоского конденсатора рассчитать теоретическое значение емкости воздушного конденсатора. Пластины считать прямоугольниками размером 16.8х13.5 см.

5. Используя измерения п.2, рассчитать для трех значений U согласно (6) емкость воздушного конденсатора C_В, найти среднее значение и погрешность. Сравнить с теоретическим значением.

6. Для измерений п.3, используя формулы (6), (7) и найденное экспериментальное значение C_В, определить диэлектрическую проницаемость ε для каждого диэлектрика.

Контрольные вопросы

1. Какие бывают виды диэлектриков и виды поляризации?

2. Что такое диэлектрическая проницаемость вещества?

3. Как понимается "физически малый объем"?

4. В каких единицах измеряется поляризованность вещества?

Литература

И.В. Савельев. Курс общей физики, т. 2, М. “Наука”, 1988 г. §§21-23.

Работа №3. Гистерезис сегнетоэлектрика

Цель работы: Изучение свойств сегнетоэлектрика, исследование петли гистерезиса сегнетоэлектрика.

Краткая теория

Особый класс диэлектриков составляют сегнетоэлектрики, которые в некотором интервале температур даже в отсутствие внешнего электрического поля имеют области самопроизвольной (спонтанной) поляризованности. Такие области называются доменами, в них дипольные моменты молекул ориентированы параллельно друг другу. В кристаллах сегнетоэлектрика имеется множество доменов с линейными размерами от 10^-4 до 10^-1 см, векторы спонтанной поляризованности которых имеют различные ориентации. Поэтому в отсутствие внешнего электрического поля суммарная поляризованность сегнетоэлектрика может быть равна нулю. При наложении на сегнетоэлектрик электрического поля происходит переориентация доменов, и суммарный вектор спонтанной поляризованности получает преимущественное направление, которое совпадает с направлением электрического поля либо образует с ним острый угол. Величина спонтанной поляризованности сегнетоэлектриков нелинейным образом зависит от внешних условий: напряженности электрического поля, температуры, механических напряжений. Наличием доменной структуры объясняются специфические особенности сегнетоэлектриков.

Диэлектрическая проницаемость сегнетоэлектриков ε намного больше, чем у обычных диэлектриков, и может достигать тысяч и десятков тысяч единиц. В отличие от обычных диэлектриков диэлектрическая проницаемость сегнетоэлектриков существенным образом зависит от напряженности электрического поля и температуры.

С

Рис.1

увеличением напряженности электрического поля Е диэлектрическая проницаемость ε сегнетоэлектриков вначале возрастает, достигая максимального значения при определенной напряженности, различной для разных сегнетоэлектриков, а затем уменьшается (Рис.1). Аналогичный вид имеет зависимость диэлектрической проницаемости от температуры. При нагревании сегнетоэлектрика диэлектрическая проницаемость достигает максимального значения при температуре Кюри, после которой разрушаются домены, сегнетоэлектрик теряет свои специфические свойства и переходит в состояние обычного диэлектрика. При охлаждении ниже температуры Кюри свойства сегнетоэлектрика полностью восстанавливаются.

Описанные свойства сегнетоэлектриков позволяют использовать их в малогабаритных конденсаторах и в специальных конденсаторах-варикондах, емкость которых в зависимости от приложенного напряжения и температуры может изменяться почти в 10 раз. Благодаря высокому значению пьезоэлектрической постоянной сегнетоэлектриков, широкое распространение получили сегнетоэлектрические пьезоэлементы.

Электрическое смещение (электрическая индукция) в диэлектрике о

(1)

пределяется соотношением:

= ε_о + ,

где – напряженность поля, - поляризованность диэлектрика (вектор поляризации).

В

(2)

сегнетоэлектриках поляризованность складывается из двух компонент:

= +

где – спонтанная поляризованность, – индуцированная поляризованность.

Индуцированная поляризованность сегнетоэлектриков происходит за счет смещения центров отрицательных и положительных зарядов атомов и молекул относительно друг друга под действием внешнего электрического поля и при не слишком сильных полях почти пропорциональна .

При изменении напряженности внешнего электрического поля поляризованность сегнетоэлектриков изменяется за счет изменения как спонтанной, так и индуцированной поляризованности.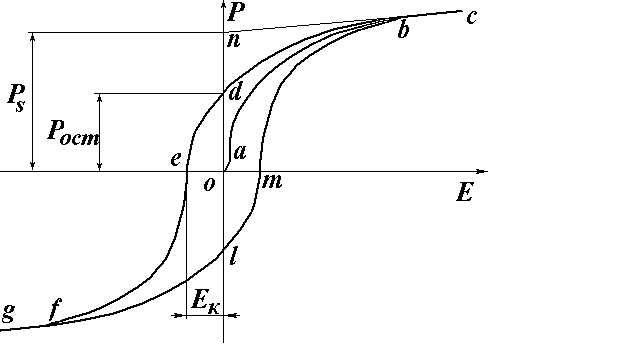

П

Рис.2

роцесс поляризации сегнетоэлектриков носит необратимый характер. В них наблюдается явление диэлектрического гистерезиса, заключающееся в том, что поляризованность сегнетоэлектрика определяется не только существующим электрическим полем, но зависит от предыдущих значений поляризованности; при этом происходит отставание изменений поляризованности и, следовательно, электрического смещения , от изменений напряженности электрического поля (Рис.2).

Первоначальная поляризация полидоменного сегнетоэлектрика происходит по кривой oabc. В слабых электрических полях наблюдается в основном индуцированная поляризованность напряженности (участок оа). При дальнейшем увеличении напряженности происходят одновременно индуцированная и спонтанная поляризация (участок ab). При некотором значении все домены окажутся ориентированными по направлению внешнего поля (точка b) и спонтанная поляризованность достигает насыщения. При дальнейшем увеличении поляризованность сегнетоэлектрика будет возрастать линейно лишь за счет индуцированной поляризованности _i. Индуцированную поляризованность можно графически вычесть, если принять во внимание, что в области не очень сильных полей она линейно зависит от напряженности поля . Тогда, экстраполируя линейный участок bc до пересечения с осью ОР, получим величину поляризованности в точке n, которая будет равна спонтанной поляризованности сегнетоэлектрика  _s (отрезок оn). Очевидно, что такой метод определения спонтанной поляризованности является приближенным. Тем не менее во многих случаях его точность оказывается достаточной.

При уменьшении поляризованность сегнетоэлектрика будет изменяться не по начальной кривой, а по кривой cbd. При значении = 0 в сегнетоэлектрике останется некоторая остаточная поляризованность _ост (отрезок оd), для снятия которой необходимо наложить поле противоположного направления до значения, называемого коэрцитивным полем или коэрцитивной силой _к (отрезок ое). При дальнейшем циклическом изменении напряженности график = f ( ) замкнется по кривой сbdefglmbc, называемой петлей гистерезиса. Форма петли гистерезиса зависит от температуры кристалла. При температурах, значительно превышающих температуру Кюри, гистерезиса нет, и поляризованность в области не очень сильных полей линейно зависит от напряженности поля.