А. В. Мальцева

Методические указания

к выполнению лабораторных работ по дисциплине "Математическое моделирование

систем электроснабжения"

Омск 2011

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

–––––––––––––––––––––––––––––––––––

А. В. Мальцева

Методические указания

к выполнению лабораторных работ по дисциплине

"Математическое моделирование

систем электроснабжения"

Утверждено редакционно-издательским советом университета

Омск 2011

УДК 621.311.001.57(075.8)

ББК 32.97 я73 + 39.217 я73

М21

Методические указания к выполнению лабораторных работ по дисциплине "Математическое моделирование систем электроснабжения" / А. В. Мальцева; Омский гос. ун-т путей сообщения. Омск, 2011. 39 с.

Изложены краткие теоретические сведения о принципах расчета и математического моделирования систем электроснабжения и их элементов. Приведены основные приемы составления и расчета параметров схем замещения линий электропередачи, силовых трансформаторов, а также матричных уравнений состояния электрической системы.

Методические указания предназначены для студентов пятого курса специальности 101600 – "Энергообеспечение предприятий", могут быть полезны студентам электромеханического факультета и слушателям факультета повышения квалификации в приобретении навыков проведения моделирования и расчетов систем электроснабжения и их элементов.

Библиогр.: 6 назв. Табл. 7. Рис. 11.

Рецензенты: доктор техн. наук, профессор

канд. техн. наук

________________________

© Омский гос. университет

путей сообщения, 2011

ОГЛАВЛЕНИЕ

Введение …………………………………………………………………………	5
Лабораторная работа 1. Исследование режима холостого хода линии электропередачи …………………………………………………………….	6
Лабораторная работа 2. Расчет линейной цепи электрической системы…..	11
Лабораторная работа 3. Моделирование силовых трансформаторов ………	17
Лабораторная работа 4. Расчет установившегося режима работы
электрической системы……………………………………………………...	25
Лабораторная работа 5. Формирование матричных уравнений состояния
электрической системы и их решение ..........................................................	31
Контрольные вопросы…………………………………………………………...	36
Библиографический список……………………………………………………..	37

Введение

Энергетика – одна из самых больших на планете искусственных систем. Её основное назначение: производство, преобразование, передача, распределение и потребление энергии (тепловой, электрической и т.д.). Важнейшей частью большой системы энергетики являются электроэнергетические системы, которые относятся к категории сложных систем.

Сложные системы – это системы, имеющие глубокие внутренние связи и состоящие из большого количества взаимосвязанных и взаимодействующих между собой элементов (генераторы, трансформаторы, линии электропередачи, электроприемники и т.д.). Любая сложная техническая система в целом обладает новыми качествами, не свойственными её отдельным элементам: например, элементы электроэнергетической системы – линии электропередачи (ЛЭП), трансформаторы, электростанции – подчиняются различным законам и алгоритмам функционирования.

Современные электроэнергетические системы (ЭЭС) содержат большое количество элементов, имеют многообразные внутренние и внешние связи и требуют большого объёма информации для описания режимов их работы.

Все это определяет целесообразность и возможность использования при управлении ЭЭС методов математического моделирования, реализуемых с использованием вычислительной техники.

Цель проведения лабораторных работ по дисциплине "Математическое моделирование систем электроснабжения" – помочь студентам приобрести практические навыки по определению характеристик компонентов электрических систем, расчету и моделированию систем электроснабжения промышленных предприятий в целом и их элементов в отдельности. Для этого в работе используется принцип "от простого – к сложному", т. е. на первых этапах идет рассмотрение элементов систем электроснабжения (линии электропередачи, трансформаторы, линейные цепи) и закрепление навыков их расчета на основе теоретической электротехники, а затем следует моделирование энергетической системы на макроуровне и ее расчет.

Выполнение изложенных в методических указаниях заданий возможно как вручную, так и с применением вычислительной техники. К защите лабораторных работ студент должен знать ответы на контрольные вопросы и уметь пояснить любые расчеты и зависимости, приведенные в отчетах.

Лабораторная работа 1

Исследование режима холостого хода линии электропередачи

Цель работы: ознакомиться со свойствами и математическими моделями линий электропередачи, построить графики напряжения и тока вдоль линии на холостом ходе, дать характеристику полученным зависимостям.

1.1. Краткие теоретические сведения

Параметры фаз линий электропередачи равномерно распределены по ее дли­не, т.е. линия электропередачи представляет собой цепь с равномерно распреде­ленными параметрами [1]. Точный расчет схемы, содержащей такую цепь, приводит к сложным вычислениям. В связи с этим при расчете линий электропередачи в об­щем случае применяют упрощенные Т- и П-образные схемы замещения с сосре­доточенными параметрами. Погрешности электрического расчета линии при Т- и П-образной схемах замещения примерно одинаковы, они зависят от длины линии.

Р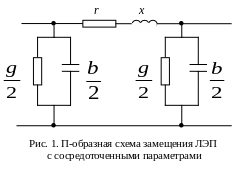 азмерность схемы электрической системы и, соответственно, системы моделирующих уравнений определяется числом узлов схемы. Поэтому в практических расчетах, в особенности с использованием ЭВМ, чаще используют П-образную схему замещения (рис. 1), имеющую одно преимущество – меньшую в 1,5 раза размерность схемы в сопоставлении с мо­делированием ЛЭП Т-образной схемой.

На схеме присутствуют следующие элементы:

r – активное сопротивление;

х – индуктивное сопротивление;

g – активная проводимость;

b – емкостная проводимость.

Допущение о сосредоточенности реально равномерно распределенных па­раметров по длине ЛЭП справедливо при протяженности воздушных линий (ВЛ), не превышающей 300–350 км, а для кабельных линий (КЛ) 50–60 км. Для ЛЭП большей длины применяют различные способы учета распределенности их па­раметров.

Активное сопротивление обуславливает нагрев проводов (тепловые потери) и зависит от материала токоведущих проводников и их сечения, определяется по формуле, Ом:

, (1)

где r₀ – удельное (погонное) активное сопротивление линии, Ом/км; является справочным данным;

l – длина линии, км.

Индуктивное сопротивление обусловлено магнитным полем, возникающим вокруг и внутри проводника при протекании по нему переменного тока. Чем боль­ше изменение потокосцепления, определяемое частотой тока, и величина индуктивности фазы, зависящая от конструкции (разветвленности) фазы и трехфазной ЛЭП в целом, тем больше ин­дуктивное сопротивление элемента. Определяется по формуле, Ом:

, (2)

где x₀ – удельное (погонное) индуктивное сопротивление линии, Ом/км; является справочным данным.

Емкостная проводимость b обусловлена емкостями между фазами, фазными проводами (жилами) и землей. Емкостная проводимость КЛ зависит от конструкции кабеля и указывается заводом-изготовителем. ЛЭП с поперечной емкостной проводимостью, потребляющая из сети опе­режающий напряжение емкостный ток, следует рассматривать как источник ре­активной (индуктивной) мощности, чаще называемой зарядной. Имея емкостной характер, зарядная мощность Q_с (ВАр) уменьшает индуктивную составляющую нагрузки, передаваемой по линии к потребителю.

Активная проводимость воздушных ЛЭП обусловлена потерями активной мощности из-за несовершенства изоляции (утечки по поверхности изоляторов, токов проводи­мости (смещения) в материале изолятора) и ионизации воздуха вокруг проводни­ка вследствие коронного разряда.

В кабельных линиях под влиянием наибольшей напряженности находятся слои поясной изоляции у поверхности жил кабеля. Чем выше рабочее напряжение кабеля, тем заметнее токи утечки через материал изоляции и нарушение ее диэлектрических свойств. Последние характеризуются тангенсом угла диэлектрических потерь, принимаемым по данным завода-изготовителя.

К характеристикам протяженных линий относятся также волновое сопротивление линии Z_c и коэффициент распространения волны γ₀, которые определяются по следующим формулам [2]:

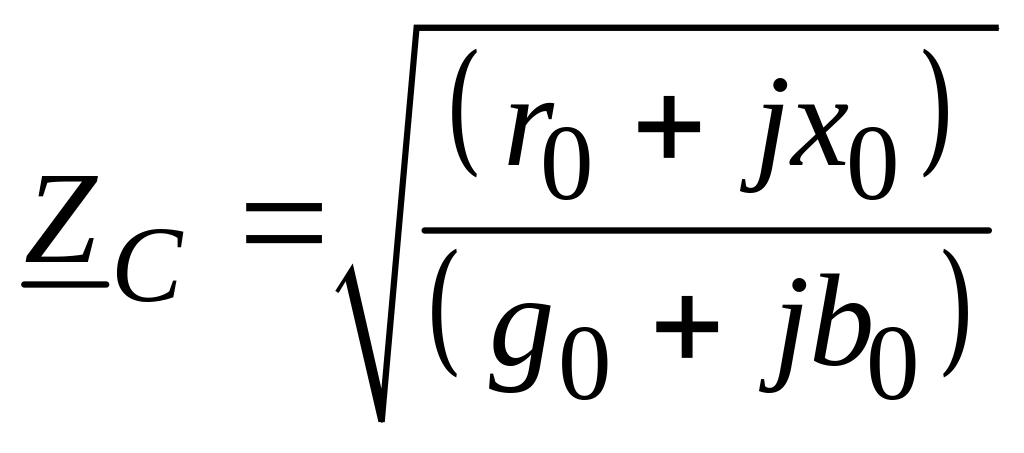(3)

и

, (4)

где g₀ и b₀ – удельные (погонные) активная и емкостная проводимости линии, Ом/км; являются справочными данными;

α₀ – коэффициент затухания волны;

β₀ – коэффициент фазы.

Формально напряжение и ток в любой точке линии можно рассматривать как результат наложения двух волн, движущихся в противоположные стороны. С течением времени волна напряжения перемещается от начала линии к ее концу; она носит название прямой или падающей волны. Волна напряжения, которая перемещается от конца линии к ее началу, носит название обратной или отраженной волны.

Напряжение в конце линии U₂ зависит от коэффициента распространения волны вдоль линии электропередачи γ₀, длины линии l и напряжения в начале линии U₁ и определяется по формуле:

. (5)

Напряжение и ток в любой точке линии, отстоящей на значение х от ее начала, определяется по формулам соответственно:

(6)

и

. (7)