2.6 Побудова алгоритму пошуку пошкоджень методом “віток і границь”

При пошуку пошкоджень в складному об’єкті, коли необхідно забезпечити мінімальну вартість реалізації алгоритму пошуку, використовують метод “віток і границь” [3].

Задача формування процедури пошуку здійснюється так.

Вважають, що об’єкт складається із довільно з’єднаних елементів, кожен з яких може знаходитись в двох станах: справний і несправний. Задана множина станів , кожен з яких характеризується - мірним вектором. Кожна -а компонента вектора є 1, якщо відсутня несправність в - ому елементі, і 0, якщо несправність є. Ймовірність знаходження об’єкта в стані позначимо через , при цьому .

Задана кінцева множина перевірок , які характеризуються константою типу 0 і 1. Вартість кожної перевірки дорівнює . Множина повністю забезпечує пошук пошкодження. Вартість перевірки не залежить від послідовності їх виконання. При пошуку об’єкт не переходить з одного стану в інший. Необхідно вибрати таку послідовність перевірок, яка забезпечує найменшу вартість пошуку. Середня вартість визначення стану об’єкта

,

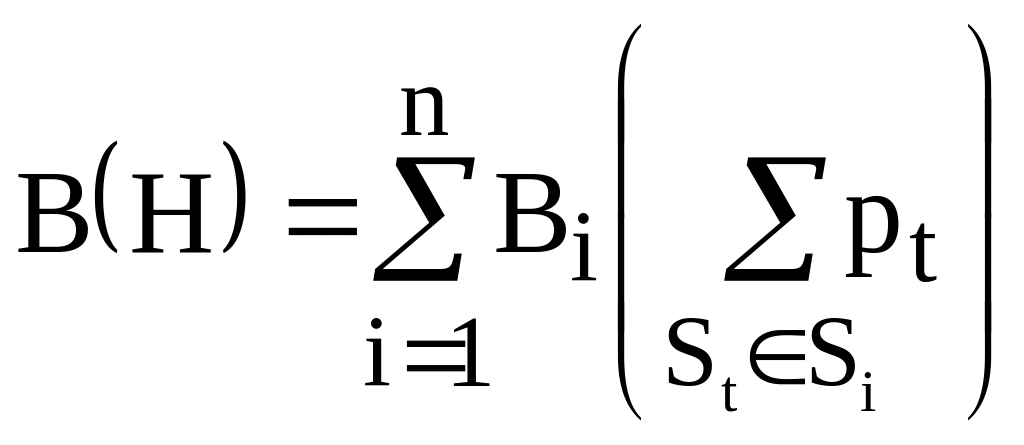де - множина станів, визначення яких здійснюється операціями, які створюють дерево з початковою вершиною .

Застосування методу віток та границь передбачає подання об’єкта у вигляді таблиці станів. Обравши будь-яку перевірку з множини і виконавши її, можна тим самим розділити множину можливих станів на дві підмножини , які відповідають константам 0 і 1 результату перевірки. Оскільки порядок отримання перевірок у вибраних підмножинах невідомий, то знайти середню вартість визначення будь-якого стану в підмножинах не можна. У зв’язку з цим, середня вартість замінюється величиною її нижньої границі:

.

На першому кроці алгоритму пошуку розраховують нижню границю середньої вартості для всіх можливих послідовностей виконання перевірок і вибирають послідовність, яка відповідає мінімальній нижній границі вартості.

На другому кроці алгоритму розраховують нижню границю вартості для кожної пари перевірок при визначенні станів із підмножин і .

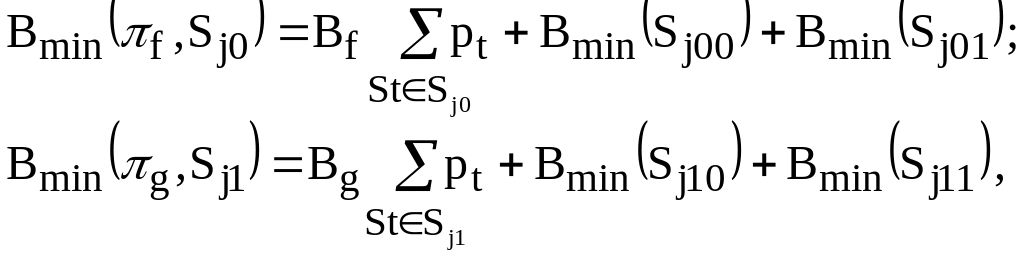
де - вартість фіксованих перевірок в підмножинах і ; подвійні цифрові індекси 00, 01, 10, 11 визначають відношення до підмножин та і, відповідно, результат (0 або 1) перевірок і в цих підмножинах. Значення нижніх границь середньої вартості кожної послідовності перевірок визначимо з виразу

.

Виконуючи аналогічні дії на наступних кроках і вибираючи кожного разу найменшу з нижніх границь вартості, здійснюють поділ до тих пір, доки не будуть в множині виділені всі підмножини, які мають не більше двох станів, і визначена послідовність перевірок. Якщо середня вартість вибраної послідовності перевірок перевищує нижню границю вартості будь-якої вартості з можливих послідовностей на будь-якому кроці, то процес повторюється.

Приклад. Об’єкт заданий таблицею функцій станів (табл. 2.8). Задана вартість окремих перевірок: ; ; ; ; , а також ймовірності станів: ; ; ; ; . Користуючись методом “віток і границь”, визначити оптимальну, за критерієм мінімальної вартості, послідовність перевірок.

Оскільки послідовність перевірок невідома, то потрібно розглянути всі можливі варіанти, і вибрати такий, який має найменшу нижню границю вартості. Побудуємо дерево можливих розв’язків і підрахуємо середню нижню вартість розв’язку. Якщо першою буде перевірка , то можливі варіанти 1-12:

Таблиця 2.8 – Таблиця станів

	0	0	1	1	1
	1	0	1	0	1
	1	1	0	0	1
	1	1	1	0	1
	1	1	1	1	0

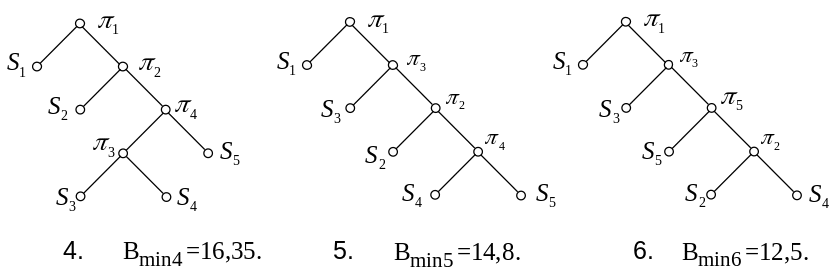
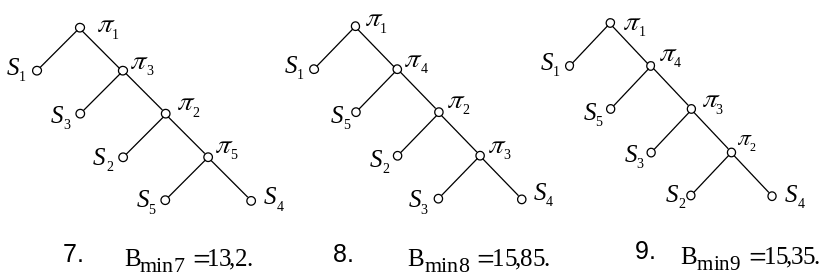
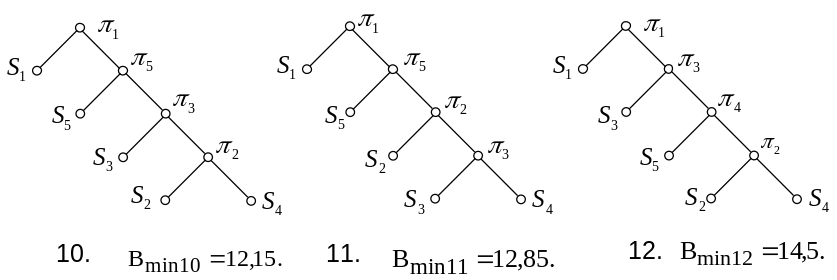
Якщо першою є перевірка , то можливі варіанти 13-18:

Якщо першою буде перевірка , то можливі варіанти 19-30:

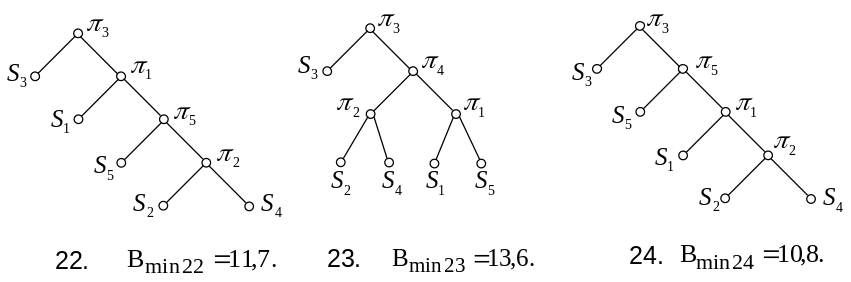
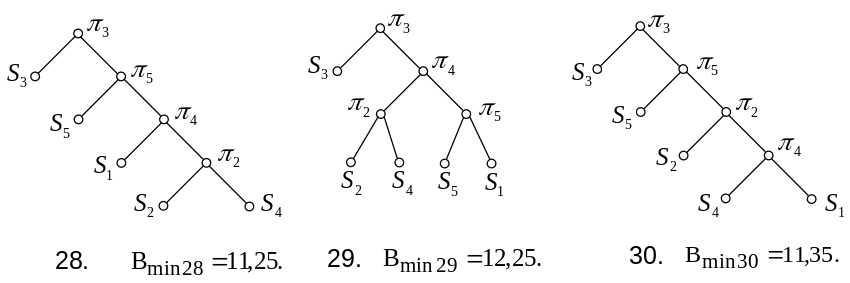
Для четвертої перевірки можливі варіанти 31-34:

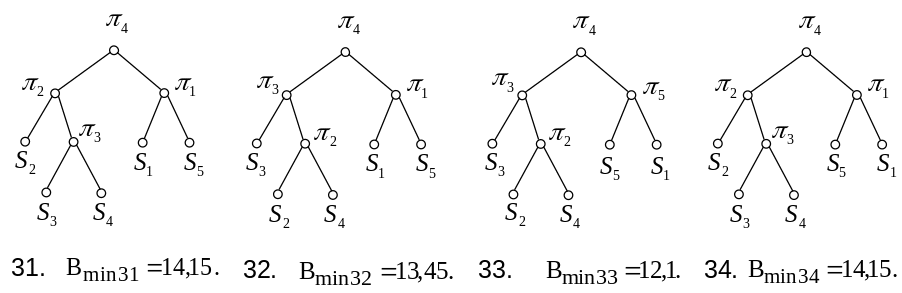
Для п’ятої перевірки можливі варіанти 35-44:

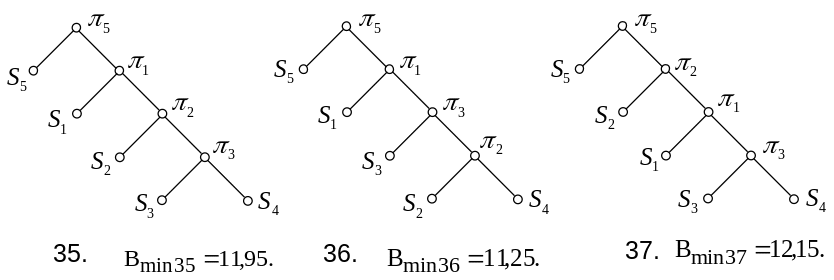
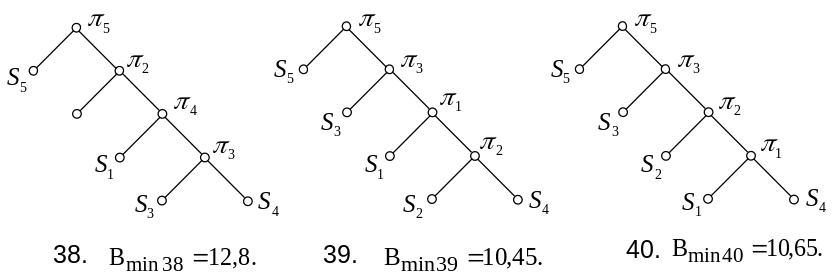
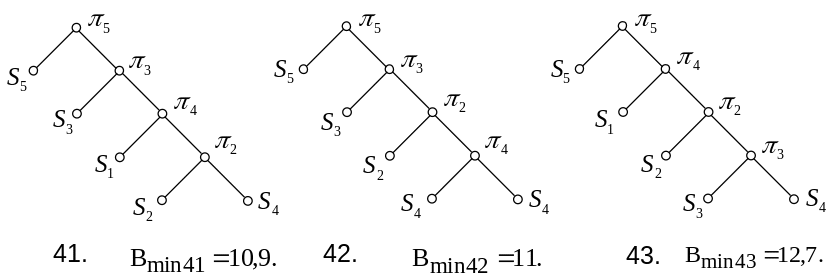
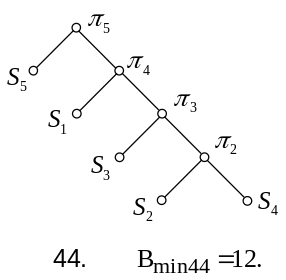
Визначимо середню нижню границю вартості для кожного із варіантів послідовності перевірок (1-44).

Дослідження наведених варіантів показало, що оптимальним є варіант № 13, який має найменшу нижню границю вартості