2. Рассмотреть сходимость гармонического ряда.

3. Решить примеры на достаточные признаки.

Литература: 1 , 4 , 8 , 10 .

Методические рекомендации: Задать ряды – это значит указать правило, закон образования его членов, по которому можно найти любой его член. Поэтому необходимо уметь по заданным членам ряда составить формулу его общего члена и наоборот. Ряды широко применяются для приближенного вычисления значений функции, определенных интегралов.

СРСП-10.

Задания: 1) Исследовать сходимость ряда с общим членом

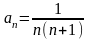
2)Законспектировать теорему Лейбница, понятия об условно и абсолютно сходящихся рядах.

Формы проведения СРСП-10: Решение задач.

Методические рекомендации: В основном мы рассматриваем ряды, члены которых имели одинаковые знаки, а для определенности считались положительными. Теперь будем считать, что члены ряда могут иметь различные знаки. Такие ряды называются знакопеременными, среди знакопеременных рядов выделим их частный случай – знакочередующиеся ряды. Их сходимость определяется теоремой Лейбница.

Литература: 1, 4, 8, 10.

СРС-10:

Задание: 1) Конспект темы «Степенные ряды», «Ряды Маклорена; разложение функций в степенные ряды».

2) Выучить разложение функций y= e^x, y= sin x, y= cos x

Методические рекомендации: Степенные ряды можно почленно дифференцировать и интегрировать, это имеет большое практическое применение. Через разложение функций в ряды Маклорена, можно приближенно посчитать значения многих выражений.

Литература: 1 , 4 , 8 , 10 .

Темы для самостоятельного изучения по дисциплине «Математика для экономистов»

№	ТЕМА	Кол-во часов	Форма контроля
	Элементы линейной алгебры. Элементы векторной алгебры и аналитической геометрии. Система линейных однородных уравнений	7	Письменная работа
	Кривые на плоскости Логарифмическое дифференцирование. Производные функции заданных в параметрическом виде.	7	Научно-исследование работа
	Предел и непрерывность. Классификация точек разрыва Элементарные функции Предел и непрерывность	7	Реферат
	Дифференциал функции. Приложения производной. Функции двух переменных	6	Письменная работа
	Методы интегрирования Приближенное вычисление определенного интеграла Двойной интеграл Неберущиеся интегралы. Приложения определенного интеграла.	6	Тест
ТЕМА	Дифференциальные уравнения. Уравнение Бернулли Ряды. Ряды Тейлора и Маклорена	6	Индивидуальные задания
	Теория вероятности. Случайные события. Случайные величины. Математическая статистика	6	Тесты
	ИТОГО	45

7. Методические указания по изучению дисциплины

Методические указания для практических (семинарских) занятий

При выполнении практических заданий надо строго придерживаться указанных ниже правил. Работа, выполненная без соблюдения этих правил, не зачитывается и возвращается студенту для переработки

1. практические задания следует выполнять в тетради чернилами синего или черного цвета, оставляя поля для замечаний рецензента

2. решения задач следует располагать в порядке номеров, указанных в заданиях

3.перед решением каждой задачи надо полностью вписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.

4.решение задач нужно излагать подробно и аккуратно, объявляя все действия.

5. после получения прорецензированной работы ( как зачтенной, так и не зачтенной) студент должен исправить в ней все отмеченные рецензентом ошибки и недочеты.

Презентация – это (представление) официальное представление вновь созданного вопроса, оценка и анализ определенной темы, который дается на рассмотрение студентам для обсуждения, споров, проведения круглых столов, диспутов. В презентации ставиться главная цель – отстоять и защитить эту тему, показать правильность выбора.

Кейсы составляются по определенным темам, где обсуждаются задачки и ситуации, отраженные в кейсах. Кейсы можно составить индивидуально или группой. После обсуждается и выносится на обзор.

Деловая игра – это целенаправленная игра, основная цель деловой игры является формирование у студентов профессиональных умений и навыков по управлению персоналом при приеме на работу. Деловая игра базируется на активизации познавательной деятельности, обучаемых в учебном процессе.

Тест – это выбор вариантов. Каждый участник данную задачу должен решить самостоятельно. Он поставлен в определенную ситуацию, и ему нужно принять много решений. При этом обстоятельства являются неблагоприятными, и все происходит в жестких временных рамках. Для данного теста участнику отводится один час, и все свои решения он должен обосновать письменно. После оценки результатов упражнения каждому участнику должна быть предоставлена возможность послетестовой беседы, чтобы выяснить и уточнить принятые им решения. Преподавателю также предоставляется возможность определить, как быстро можно заставить участника поменять свою позицию или до каких пор он отстаивает свое решение.

Контрольная работа – это самостоятельная работа студентов на СРСП. Она выполняется письменно. Вопросы можно представить в виде тестов, вопросов по вариантам или каждому индивидуально. Контрольная работа выполняется по пройденным темам. Здесь определяется, насколько студент самостоятельно готовился к определенной теме. Ответы должны быть четкими и краткими, с определенными примерами и оценивается по пятибалльной шкале.

Методические указания по проведения СРСП

С) самостоятельная работа студентов с преподавателями (СРСП)

СРСП выполняет две функции: консультативную и контролирующую. СРСП – это совместная работа студента и преподавателя, поскольку учебные занятия проводятся в диалоговом режиме, например тренинг, дискуссия, деловая и дидактические игры, презентация, составление кейса, разработка индивидуального, группового проектов и т.п.

К каждому СРСП должны быть подготовлены материалы (кейсы, ролевые игры, тесты, кроссворды и т.д.), которые позволяют детализировать какие-либо вопросы, расширять их, отрабатывать навыки анализа тех или иных ситуаций, решать задачи и др.

9. Материалы для самостоятельной работы обучающегося:

- наборы текстов домашних заданий,

- материалы самоконтроля по каждой теме,

- задания по выполнению текущих видов работ, рефератов и других домашних заданий с указанием трудоемкости и литературы

- кейсы

- кроссворды

- решение задач

- упражнения

10. Методические указания по прохождению учебной, производственной и преддипломных практик, формы отчетной документации (если требует специфика дисциплины)

11. Материалы по контролю и оценке учебных достижений обучающихся

- схема оценки знаний

- письменные контрольные задания

- тестовые задания

- перечень вопросов для самоподготовки

- экзаменационные билеты