- •Западно-Казахстанский государственный университет им. М. Утемисова
- •Учебно-методический комплекс дисциплины «Математика для экономистов»
- •Курс – 1
- •Всего – 87 часов Уральск
- •Западно-Казахстанский государственный университет им. М. Утемисова
- •Программа курса (sillabus) «Математика для экономистов»
- •Курс – 1
- •Всего – 87 часов Уральск
- •1.1 Данные о преподавателе Садыкова г.А. – ст. Преподаватель
- •1.2 Данные о дисциплине Математика для экономистов
- •1.3 Введение
- •2. Программа обучения по дисциплине - syllabus
- •Кредит час 2
- •Кредит час 1 Лекция №5
- •Кредит час 3
- •Кредит час 3
- •Кредит час 1
- •Кредит час 2
- •Практическое занятие№ 8
- •Кредит час 1
- •Неделя 11 Кредит час 1
- •Кредит час 2
- •Кредит час 1
- •Кредит час 2
- •Лекция №25
- •Лекция №26
- •Лекция №27
- •3. График выполнения и сдачи заданий по дисциплине Математика для экономистов
- •4. Карта учебно-методической обеспеченности дисциплины
- •Лекционный комплекс:
- •Лекция №1. Тема: «Определители 2,3 порядков. Системы линейных уравнений. Метод Крамера».
- •Свойства определителей 3-го порядка
- •Системы линейных уравнений.
- •Правило Крамера.
- •Миноры и алгебраические дополнения
- •Определители высших порядков, их вычисление.
- •Теорема о разложении определителя
- •Лекция №2. Тема: «Матрицы, матричный метод решения слу».
- •Виды матриц.
- •Действие над матрицами.
- •Обратная матрица.
- •Матричный метод решения слу
- •Лекция №3. Тема: «Ранг матрицы. Метод Гаусса. Система m уравнений с n неизвестными».
- •Системы линейных уравнений.
- •Критерий совместности и единственности решения слу. Теорема Кронекера-Капелли.
- •Лекция №№ 4-7 Векторы, линейные операции над векторами. Линии первого порядка на плоскости.
- •4.1. Векторы. Основные понятия и простейшие действия над векторами. Базис и координаты.
- •4.2. Скалярное, векторное, смешанное произведение векторов. Свойства скалярного произведения.
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •4.3. Понятие об уравнении линии. Различные уравнения прямой.
- •Частные случаи общего уравнения прямой
- •Практические занятия к теме 2.
- •Контрольные вопросы и задания к теме 2.
- •Задачи к теме 2
- •Производная функции в точке. Таблица производных, правила дифференцирования. Дифференциал функции.
- •5.1. Механический, геометрический, экономический смысл производной.
- •5.2. Основные правила дифференцирования.
- •5.3. Производные высших порядков
- •5.4. Дифференциал.
- •5.5 .Геометрический смысл дифференциала.
- •Практические занятия к теме 5.
- •Контрольные вопросы и задания к теме 5.
- •Задания к теме 5.
- •Лекция №№ 15-17 Неопределенный интеграл.
- •7.1. Первообразная и неопределенный интеграл. Основные свойства.
- •Неопределенный интеграл представляет собой семейство функций
- •Из определения неопределенного интеграла следуют следующие свойства:
- •Методы интегрирования
- •7.2. Метод замены переменной.
- •7.3. Метод интегрирования по частям.
- •Проинтегрируем обе части
- •7.4. Интегрирование рациональных дробей.
- •7.5. Метод неопределенных коэффициентов в интегрировании рациональных дробей.
- •1 Случай.
- •2 Случай.
- •7.6. Интегрирование некоторых тригонометрических выражении.
- •7.7. Интегрирование некоторых видов иррациональностей.
- •Практические занятия к теме 8.
- •Контрольные вопросы и задания к теме 8.
- •Задания к теме 7. Вычислить интегралы:
- •Лекция №№ 19-20 Ряды. Числовой ряд. Сходимость и сумма числового ряда. Необходимое условие сходимости числового ряда.
- •Достаточные признаки сходимости: признаки Даламбера, Коши и другие.
- •10 Признак Даламбера.
- •20 Интегральный признак Коши.
- •4О. Признак сравнения.
- •Имеем ряд (2)
- •Функциональные ряды.
- •На основании признака Даламбера
- •Степенной ряд. Разложение функции в ряд Тейлора-Маклорена.
- •Ряд Фурье. Разложение функции в тригонометрический ряд Фурье.
- •Практические занятия к теме 11.
- •Контрольные вопросы и задания к теме 11.
- •Задания к теме 11.
- •Лекция №№ 21-24 Дифференциальные уравнения. Дифференциальные уравнения. Основные понятий, определения и уравнения с разделяющими переменными.
- •Дифференциальные уравнения первого порядка.
- •Уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения первого порядка.
- •Линейные дифференциальные уравнения первого порядка.
- •Уравнение Бернулли.
- •Линейные однородные дифференциальные уравненияс постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения II порядка с постоянными коэффициентами.
- •Системы обыкновенных дифференциальных уравнений.
- •Практические занятия к теме 10.
- •Контрольные вопросы и задания к теме 10.
- •Задания к теме 10.
- •6. Планы семинарских (практических) занятий, планы занятий в рамках срсп и срс
- •Семинар 2 Тема: Матрицы, матричный метод решения слу. Метод Гаусса.
- •Семинар- 3 Тема: « Векторы, линейные операции над векторами. Линии 1- го порядка на плоскости».
- •Семинар-6 (1 ч) Тема: Функции нескольких переменных.
- •Семинар 7 Тема: Интегральное исчисление. Неопределенный интеграл.
- •Семинар 8 Тема: Интегральное исчисление. Определенный интеграл.
- •2. Рассмотреть сходимость гармонического ряда.
- •Темы для самостоятельного изучения по дисциплине «Математика для экономистов»
- •Политика выставления оценки:
- •Знания, умения и навыки студентов оцениваются следующим образом:
- •Вопросы для проведения контроля знаний студентов по темам и экзамена
- •20. Даны координаты вершин треугольника авс
- •Примерный перечень тестовых вопросов для промежуточного и итогового контроля.
- •Примерные экзаменационные тестовые задания Вариант *
- •Список литературы
- •Дополнительная литература.
- •4. Глоссарий по дисциплине Математика для экономистов
Свойства смешанного произведения
1. (а*в)∙c=a(в*c) (сочетательный закон).
2. (а*в)∙c=-(в*а)∙c (закон круговой переместительности).
(в*с)∙а=-(с*в)∙a
(с*а)∙а=-(а*с)∙в
3. (а1+,а2)в∙с=a1∙в∙c+ a2∙в∙c
4. (λа)∙в∙c=a.(λв)∙c=a∙в.(λс)=λ∙(a∙в∙c) (распределительный относительно числового множителя закон).
Если векторы а.в.с заданы своими прямоугольными координатами а={x1; y1; z1} , в={x1; y1; z1}, с={x1; y1; z1}, то их смешанное произведение вычисляется следующим образом:
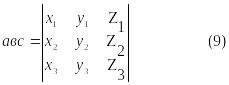
4.3. Понятие об уравнении линии. Различные уравнения прямой.
Пусть дано уравнение
у=ƒ(x), (10)
а в системе ОХУ дана линия Z .
Определение. Если координаты любой точки линии удовлетворяют уравнению у=ƒ(x), а координаты точек, не лежащих на линии , не удовлетворяют данному уравнению, то уравнение (1) называется уравнением линии.
Уравнение вида (10) называется уравнением в явном виде, в неявном виде его вид F(x;y)=o.
Например:у=5/6х –уравнение линии в явном виде, 5х-6у=o-неявный вид этого же уравнения.
Определение. Всякий вектор, перпендикулярный данной прямой, называется нормальным вектором.
 n
ℓ
n
ℓ
Нормальный вектор обозначается через n, каждая прямая имеет бесчисленное множество нормальных векторов.
Пусть задан нормальный вектор n={A;B} и точка М0(x0;y0) некоторой прямой а на координатной плоскости ОХУ.

Требуется составить уравнение прямой по этим данным. Выберем произвольную точку М(x;y) прямой а.Составим вектор М0 М ={x-x0; y- y0 }, n перпендикуляр М0 М, т.к. вектор n нормальный вектор прямой а, то он перпендикулярен любому вектору на прямой а. Отсюда следует, что скалярное произведение n∙М0 М=o, т.е. в координатной форме:
А(x-x0 )+В(y- y0) =0 (11)
Получили уравнение прямой, проходящее через данную точку, перпендикулярно вектору n.
Раскроем скобки в (11):
Ах+Ву-Ах0-Ву0=0, обозначим – Ах0-Ву0=С
Ах+Ву+С=0 (11)- это общее уравнение прямой.
Частные случаи общего уравнения прямой
1. При С=0 уравнение Ах+Ву=0 определяет прямую, проходящую через начало координат
2. При А=0 уравнение Ву+С=0 определяет прямую, параллельную оси Ох.
При В=0 уравнение Ах+С=0 определяет прямую, параллельную оси Оу.
3. При А=С=0 уравнение Ву=0 определяет ось Ох.
При В=С=0 уравнение Ах=0 определяет ось Оу.
Без вывода запишем уравнение прямой, проходящей через две точки М1 (x1;y1) и М2 (x2;y2);
(х -x1)/( x2-x1) =(у -у1)/( у2-у1).
Определение. Всякий вектор параллельный данной прямой, называется направляющим вектором этой прямой.
Пусть задан направляющий вектор прямой а={ℓ;m} и точка М0(x0;y0). Тогда каноническое уравнение прямой записывается следующим образом.
(х –x0)/
ℓ= (у -у![]() )/
m
(12)
)/
m
(12)
Определение. Углом наклона прямой а к оси ОХ называется угол между положительным направлением оси ОХ и направляющим вектором прямой а.

у
а
а
а φ х
φ-угол наклона.
Определение. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси ОХ.
Обозначается k=tgφ.
Тогда уравнение прямой с угловым коэффициентом k и проходящее через данную точку М0(x0;y0) следующее: y- y0= k (х –x0). (13)
Угол между двумя прямыми на плоскости
Условия параллельности и перпендикулярности прямых
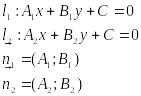
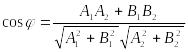
Условие параллельности прямых
![]() и
и
![]()
![]()
Условие перпендикулярности прямых и
![]()
Расстояние от точки до прямой
Т/н: расстояние
![]() от
точки М
от
точки М![]() до
прямой
до
прямой
![]() ,
заданной общим уравнением
,
заданной общим уравнением

Деление отрезка в данном
отношении
![]() .
.
![]()
2.4. Плоскость. Различные виды уравнении плоскости. Прямая в пространстве. Уравнение плоскости, проходящей через заданную точку.
![]()
![]()
![]()
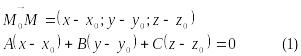
- уравнение плоскости, проходящей через заданную точку и перпендикулярной вектору .
Общее уравнение плоскости
![]()
Раскрыв скобки, и обозначив -![]() ,
,
Получаем
![]() -
общее уравнение плоскости.
-
общее уравнение плоскости.
Уравнение плоскости, проходящей через три точки

Угол между двумя плоскостями.
Условия параллельности и перпендикулярности плоскостей
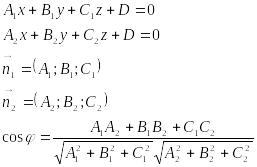
Условие параллельности плоскостей
![]()
Условие перпендикулярности плоскостей
![]()
Расстояние от точки до плоскости
Т/н: расстояние
от
точки М![]() до
плоскости, заданной общим уравнением
до
плоскости, заданной общим уравнением
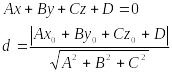
Прямая в пространстве
Прямая может быть задана уравнениями двух плоскостей.
![]()
пересекающихся по этой прямой.
Уравнения прямой, проходящей
через две точки
![]() и
и
![]()
![]()
Канонические уравнения прямой.

Параметрические уравнения прямой в пространстве
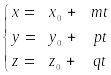
Угол между прямыми.

2.5. Простейшие кривые второго порядка.
Определение. Кривыми второго порядка на плоскости называются линии, которые аналитически определяются уравнениями второй степени относительно переменных координат Х и У.
Общее уравнение линии второго порядка имеет вид :
Ах2+2Вху+Су2+2Dх+2Еу+F=0.
К ним относятся окружность, эллипс, гипербола, парабола.
Определение. Окружностью радиуса R c центром в т. М называют множество всех точек плоскости, равноудаленных от точки М.
Пусть центр окружности задан в точке О1(x1;y1), радиус равен R. Тогда уравнение окружности принимает вид:
( х
–x1)
2+ (у –у1)2=
R2
х
–x1)
2+ (у –у1)2=
R2
у
![]()
![]() х
х
Определение. Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний от двух заданных точек, называемых “фокусами”, есть величина постоянная и равная 2а.
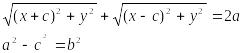
![]() –
каноническое уравнение
–
каноническое уравнение
(х2 /а2 )+(у2 /в2 )=1 –
каноническое уравнение эллипса.
а –большая полуось
в –малая полуось
F1 (-с; о), F2 (с; о)-фокусы.
Определение. Гиперболой называется множество точек плоскости, для каждой из которых разность расстояний до двух данных точек плоскости постоянна и равна 2а. Данные точки называются фокусами параболы.
(х2 /а2)-(у2 /в2 )=1-каноническое уравнение гиперболы.
![]()

Прямые у=±(в/а)х называются асимптотами гиперболы.
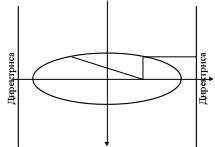
Определение. Параболой называется множество точек плоскости, для каждой из которых расстояние до заданной точки равна расстоянию до заданной прямой, не проходящей через данную точку. Данная точка называется фокусом параболы, данная прямая называется директрисой. Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается р. Канонические уравнение параболы имеют следующий вид:
у2 =2рх (парабола симметрична относительно оси ОХ)
х2 =2ру (парабола симметрична относительно оси ОУ)