Раздел 1. Введение в эконометрику

Тема 1.1. Основные понятия теории вероятностей и статистики, применяемые в эконометрике

Решение типовых задач

Задача 1. На станции технического обслуживания анализи­руются затраты времени на ремонт автомобилей. На основании данных, полученных по 100 автомобилям, выяснилось, что для 25 из них требуется 1 ч для проведения профилактических работ. Мелкий ре­монт требуется для 40 автомобилей, что занимает 2 ч. Для 20 авто­мобилей требуется ремонт с заменой отдельных узлов, что занимает в среднем 5 ч. 10 автомобилей могут быть отремонтированы за 10 ч. Для 5 автомобилей необходимое время ремонта составляет 20 ч.

Задание: Построить закон распределения СВ X — времени обслуживания случайно вы­бранного автомобиля. Определить функцию распределения F(х) и построить ее график.

Решение:

Х	1	2	5	10	20
pi	0,25	0,40	0,20	0,10	0,05

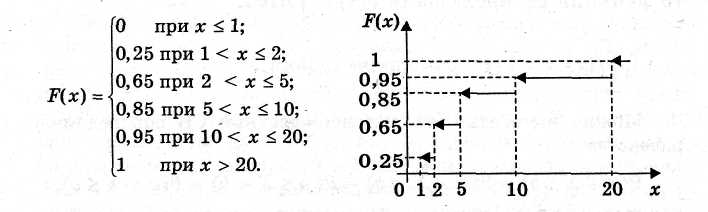Функция распределения F(х) и ее график имеют вид:

Задача 2. На основе продолжительных наблюдений за весом X пакетов орешков, заполняемых автоматически, установлено, что стандартное отклонение веса пакетов σ = 10 г. Взвешено 25 пакетов, при этом их средний вес составил х_ср = 244 г.

Задание: В каком интервале с надежностью 95 % лежит истинное значение среднего веса пакетов?

Решение:

Логично считать, что СВ X имеет нормальный закон распределе­ния:

X ~ N(m, 10). Для определения 95% -го доверительного интервала найдем критическую точку u_α/2 = u₀₀₂₅ по таблице функции Лапласа по соотно­шению

Ф(u_0,0,25)=0,95/2=0,475 => u_0,025= 1,96.

Тогда по формуле Х_ср± u_α/2σ/√n построим доверительный интервал:

(244-1,96*10/5; 244+1,96*10/5) или (240,8; 247,92).

Задача 3. Задание: В условиях задачи 2 проверить гипотезу М(Х) = 250 г при уровне значимости α = 0,05. Если данное утверждение не­верно, то станок-автомат требует подналадки.

Решение:

Н₀: m = 250;

H₁: m ≠ 250.

По формуле U=(x_ср–m₀)/(σ/√n) по данным выборки строим статистику

U = (244-250)/(10/√25)=-3. В данном случае используется двусторонняя критическая область. По таблице функции Лапласа найдем критическую точку u_α/2 = u_0,025= 1,96. Так как |U_набл| = 3 > 1,96 = u_кр, то Н_о долж­на быть отклонена в пользу H₁. Это свидетельствует о том, что станок требует подналадки. Аналогичный ответ можно получить, используя интервальную оценку (240,8; 247,92), найденную в задаче 2. Если гипотетическое значение 250 не принадлежит данному интервалу, то обоснован вывод о ложности гипотезы Н₀.

Задача 4. Анализируется доход X фирм в отрасли, имеющий нормальное распределение. Предполагается, что средний доход в дан­ной отрасли составляет не менее 1 млн. $. По выборке из 49 фирм полу­чены следующие данные: х_ср= 0,9 млн. $ и S = 0,15 млн. $.

Задание: Не противо­речат ли эти результаты выдвинутой гипотезе при уровне значимости α = 0,01?

Решение:

H₀: m = 1;

H₁: m< 1.

Для проверки гипотезы Но строим критерий Т_набл = (х_ср–m ₀)/(S/√n)=

=(0,9-1)/(0,15/7)= -4,67.

Критическую точку левосторонней критической области опреде­ляем по таблице критических точек распределения Стьюдента t_кр = -t_0,01,48=-2,404. Поскольку T_набл = -4,67 < -2,404 = t_кр, то Н_о должна быть отклонена в пользу H₁, что дает основание считать, что средний доход в отрасли меньше, чем 1 млн. $.

Задача 5. В университете проведен анализ успеваемости среди студентов и студенток за последние 25 лет. СВ X и У - соответственно их суммарный балл за время учебы. Получены следующие результаты: х_ср = 400; S_х²= 300; у_ср= 420; S_у²= 150.

Задание: Можно ли утверждать, что девуш­ки в среднем учатся лучше ребят? Принять α = 0,05.

Решение:

Для ответа на данный вопрос фактически необходимо проверить следующую гипотезу:

Н_о : М(Х) = M(Y);

H₁ : M(X) < M(Y).

По формуле 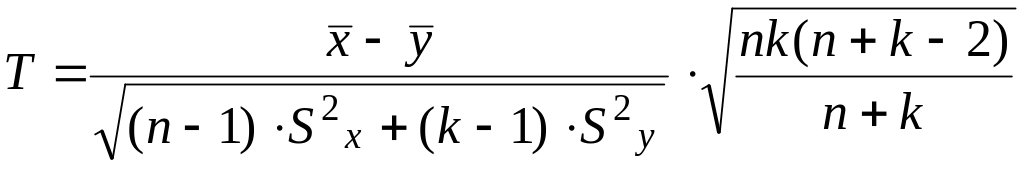строим статистику Т с учетом, что n= k = 25:

t_кр= -t_{0,05; 25+25-2} = -1,68.

Поскольку Т_набл = - 4,71 < -1,68 = t_кр, то Н_о должна быть откло­нена в пользу H₁, что дает основание утверждать, что в данном универ­ситете девушки в среднем учатся лучше ребят.

Задача 6. Задание: В условиях задачи 5 определите, есть ли осно­вания считать, что дисперсии двух СВ X и Y существенно отличают­ся друг от друга (т.е. разброс оценок у студентов больше, чем у сту­денток).

Решение:

Из условий задачи строится следующая гипотеза:

Н₀: σ²_х = σ²_у;

Н₁: σ²_х > σ²_у.

Для проверки гипотезы по формуле F = S²_x / S²_y определяется статисти­ка F_набл = 300/150 = 2. Критическая точка распределения Фишера F_кр= _0,05;24;24= =1,98. Поскольку F_набл = 2 > 1,98 = F_кр, то Н_о должна быть отклонена в пользу Н₁, и имеются основания считать, что разброс в оценках у студентов данного университета существенно больше раз­броса в оценках у студенток.

Задача 7. Точность работы станка-автомата, заполняющего па­кеты порошком, определяется совпадением веса пакетов. Дисперсия веса не должна превышать 25 (г)².

По выборке из 20 пакетов определе­на исправленная дисперсия:

г ².

Задание: Определите, требуется ли срочная подналадка станка. Принять α = 0,05.

Решение:

Сформулируем нулевую и альтернативную гипотезы, соответст­вующие условию задачи:

Н_о : σ² = 25;

H_i : σ² > 25.

Рассчитаем наблюдаемое значение критерия χ² в соответствии с

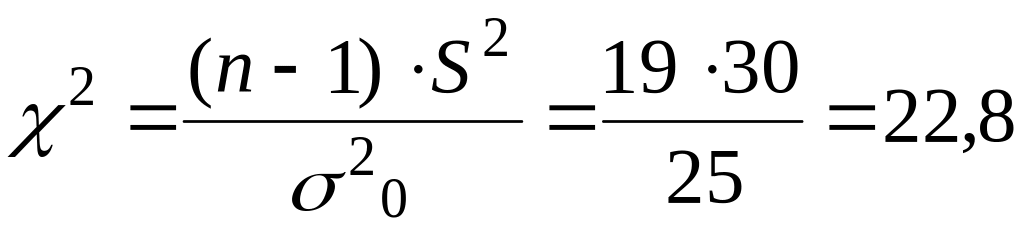
χ²_кр= χ²_0,05;19=30,14.

Так как χ²_набл=22,8 < 30,14 = χ²_кр, то нет оснований для отклонения Н₀. Другими словами, имеющиеся данные не дают основания считать, что станок требует срочной подналадки.

Задача 8. Определяется наличие линейной зависимости между уровнями инфляции (X) и безработицы (Y) в некоторой стране за 11 лет. По статистическим данным рассчитан выборочный (эмпириче­ский) коэффициент корреляции r_ху = -0,34. Задание: Существует ли значимая линейная связь между указанными показателями в данной стране на рассматриваемом временном интервале? Принять α = 0,02.

Решение:

Для ответа на вопрос проанализируем следующую гипотезу:

Н₀: ρ_ху = 0;

Н₁: ρ_ху ≠ 0.

По формуле .

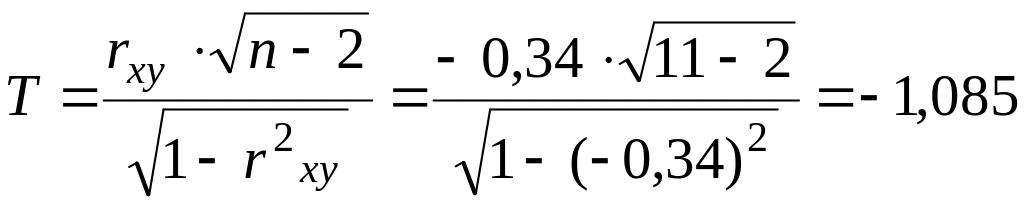С помощью таблицы критических точек распределения Стьюдента определим t _α/2;n-2 = t _0,01;9 = 2,821. Поскольку ‌‌ ‌|Т_набл| = 3,254 < 2,821, то коэффициент корреляции r_ху статистически не значим. Следовательно, ρ_ху существенно не отличается от нуля, и между уровнями инфляции (X) и безработицы (У) не существует определенная отрица­тельная линейная зависимость.

Задача 9. Автомат, работающий со стандартным отклонением σ = 5 г, фасует чай в пачки. Проведена случайная выборка объемом n = 30 пачек. Средний вес пачки чая в выборке Х_ср = 101 г.

Задание: Найдите до­верительный интервал для среднего веса пачки чая в генеральной со­вокупности с доверительной вероятностью р = 95%.

Решение:

р = 0,95 => α = 1 - р = 1 - 0,95 = 0,05 => u_α/2 = u_0,025 => Ф(u_0,025)=0,95/2 = 0,475 => u_0,025 = 1,96.

Х_ср± u_α/2σ/√n = 101 ± 1,96*5/√30 ≈ 101 ± 1,79, то есть искомый интервал (99,21; 102,79).

Задача 10. Задание: По исходным данным задачи 9 определить, каким должен быть объем выборки, чтобы ширина доверительного интервала была ± 1 грамм.

Решение:

u_α/2σ/√n ≤ 1 => √n ≥ u_α/2σ => n ≥ (u_α/2σ)² = (1,96*5)² = 96,04, то есть минимальный объем выборки равен 97. Так как объем первоначаль­ной выборки равен 30, то объем новой выборки равен 97 – 30 = 67 пачек.

Находим среднюю для объединенной выборки в 97 пачек (нахо­дим именно среднюю для выборки в 97 единиц, а не среднее арифме­тическое средних для выборок объемов 30 и 67 пачек) и получаем доверительный интервал для средней в генеральной совокупности Х_ср ±1.

Задача 11. Проведена выборка объема n = 2000 шт. 150 из них оказались бракованными.

Задание: Найти доверительный интервал доли бра­кованных изделий в генеральной совокупности для доверительной вероятности р = 95%.

Решение:

Производится выборка объема n. Для нее вычисляется выборочная доля р - доля объектов, обладающих этим свойством. Тогда при выполнении условий nр^ ≥ 5, n(1-р^) ≥ 5 доверительный интервал для ге­неральной доли задается формулой р^ ± u_α/2(√p^(l-p^)/n).

p^ = 150/2000 = 0,075

nр^ = 2000*0,075 = 150 > 5.

n(1-p^)= 2000*(1-0,075) = 1850 > 5

Оба условия выполнены.

р = 0,95 => α = 1 - р = 1 - 0,95 = 0,05 => u_α/2 = u_0,025 => Ф(u_0,025)=0,95/2 = 0,475 => u_0,025 = 1,96.

р^ ± u_α/2(√p^(l-p^)/n)= 0,075 ± 1,96(√0,075(1 - 0,075)/2000) ≈

≈ 0,075 ± 0,012, то есть искомый интервал (0,063; 0,087).

Задача 12. Задание: По исходным данным задачи 11 определить объем выборки, при котором ширина доверительного интервала будет ±0,005.

Решение:

р^ ± u_α/2(√p^(l-p^)/n) ≤ 0,005 => (u_α/2)²p^(l – р^)/n < 0,005² = 0,000025 => n ≥ (u_α/2)²p^(l – р^)/0,000025 ≈ 1,96²*0,075*(1 - 0,075)/0,000025 ≈ 10660, то есть минимальный объем выборки равен 10660.

Так как объем первоначальной выборки равен 2000, то объем но­вой выборки равен 10660 - 2000 = 8660 деталей. Находим выбороч­ную долю бракованных изделий p^ для объединенной выборки в 10660 деталей и получаем доверительный интервал для доли бракованных изделии в генеральной совокупности р ± 0,005.

Задача 13. Проводились испытания нового лекарства. В экспе­рименте участвовали n₁ = 3000 мужчин и n₂ = 3500 женщин. У 50 муж­чин и 110 женщин наблюдались побочные эффекты. Можно ли ут­верждать, что побочные эффекты от нового лекарства у женщин возникают чаще, чем у мужчин? Доверительная вероятность р = 95%.

Выборочные доли р^₁ = 50/3000 ≈ 0,017, р^₂ = 110/3500 ≈ 0,031.

H₀: p₁=p₂ (генеральные доли одинаковы).

H₀: p₁<p₂

Проведем левостороннюю проверку. α = 1- р = 1- 0,95 = 0,05 => u_α = =u_0,05 => Ф(u_0,05)=0,90/2 = 0,450 => u_0,05 = 1,645 => граничная точка -1,645. Выборочная доля для объеди­ненной выборки p_ср = (50 + 110)/(3000 + 3500) ≈ ≈0,025.

Статистика u = (p₁^-p₂^)/КОРЕНЬ(p_ср*(1- p_ср)*(1/n₁+1/n₂))=

=(0.017-0.031)/КОРЕНЬ(0,025*(1-0,025)*(1/3000+1/3500))≈-3,604

Отсюда, поскольку u_набл < u_крит (-3,604<-1,645) гипотеза Н₀ отклоняется в пользу альтернативной гипотезы Н₁ на уровне значимости 5%. Побочные эффекты от нового лекарства у женщин возникают чаще, чем у мужчин.