11.5. Определение и вычисление поверхностных интегралов II-го рода

Пусть в точках двухсторонней поверхности задана непрерывная функция . Выберем на поверхности определенную сторону. Разобьем поверхность сетью произвольно проведенных кривых на части с площадями , , …, .

В каждой части выберем по произвольной точке и вычислим в них значения данной функции. Эти значения умножим на площади проекций частей на плоскость Оху. При этом числу приписывается определенный знак, а именно, если в точках нормаль, отвечающая выбранной стороне поверхности, составляет с осью Oz острый угол, то через обозначаем площадь проекции , взятую со знаком плюс, если же эта нормаль составляет с осью Oz тупой угол, то под будем понимать площадь этой проекции, взятую со знаком минус. Составим интегральную сумму всех таких произведений:

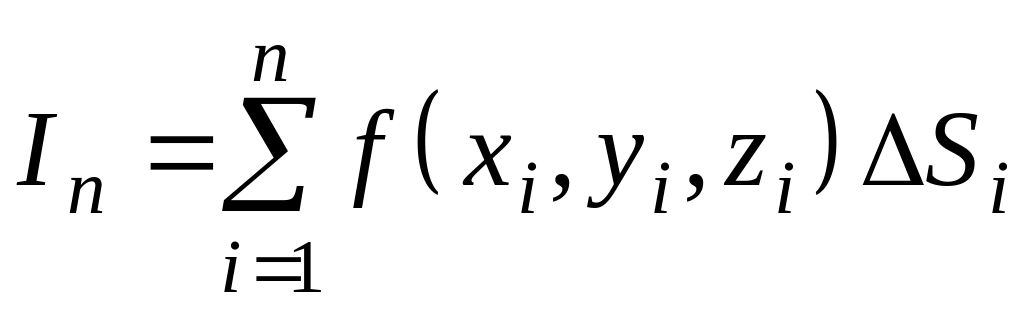. (11.5.1)

О п р е д е л е н и е. Интегралом 2-го рода от функции по поверхности называется предел суммы (11.5.1) при , где - наибольший из диаметров элементарных частей .

. (11.5.2)

Аналогично определяются интегралы:

, ,

причем для выбора знака проекции служит угол между нормалью, отвечающей выбранной стороне, и осью Оу или Ох.

Наиболее общим интегралом 2-го рода является интеграл

,

где P, Q, R – функции от x, y, z, определенные и непрерывные в точках двухсторонней поверхности .

Интегралы 2-го рода вычисляются следующим образом. Если поверхность однозначно проецируется в область плоскости Оху и - ее уравнение, то

, (11.5.3)

где справа в этой формуле стоит двойной интеграл по области . Знак плюс берется в этом случае, когда на выбранной стороне поверхности , и знак минус, когда .

Аналогично, если однозначно проецируется в область

(или ) на плоскости Oxz (или Oyz), т. е. может быть задана уравнением (или , то

, (11.5.4)

, (11.5.5)

где в случае (11.5.4) берется знак , а в случае (11.5.5) – знак .

, , - направляющие косинусы нормали, направленной в ту сторону поверхности, по которой берется интеграл 2-го рода.

Пример. Вычислить , где - верхняя сторона поверхности , отсеченной плоскостями , .

Решение.

, , т.е.

- верхняя часть цилиндрической поверхности с образующей, параллельной оси Оу и направляющей – окружностью в плоскости Oxz. - плоскость Oxz, - плоскость, параллельная плоскости Oxz.

Нормаль в точке М, соответствующая указанной стороне поверхности, составляет с осью Oz острый угол , поэтому в формуле для вычисления этого интеграла надо взять плюс. Проекцией данной поверхности на плоскость Oxу является прямоугольник, определяемый неравенствами , .

.

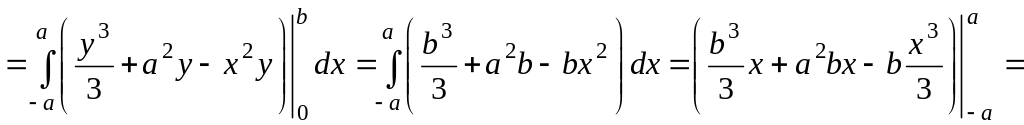
11.6. Площадь поверхности. Определение поверхностных интегралов I-го рода, их свойства и вычисление

Пусть дана функция непрерывная на некоторой гладкой поверхности . Разобьем эту поверхность сетью произвольно проведенных кривых на части с площадями , , …, .

В каждой из этих частей выберем произвольно по точке , вычислим значения функции в этих точках и составим интегральную сумму

. (11.6.1)

Обозначим через - наибольший их диаметров элементарных частей поверхности .

О п р е д е л е н и е. Интегралом 1-го рода от функции по поверхности называется предел интегральной суммы (11.6.1) при .

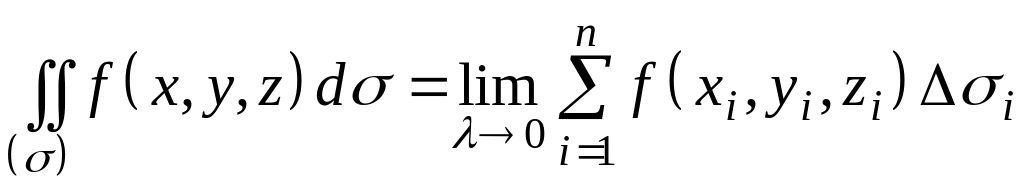. (11.6.2)

Интеграл 1-го рода обладает свойствами, аналогичными свойствам криволинейных интегралов 1-го рода.

Если и функцию f рассматривать как поверхностную плотность массы материальной поверхности , то интеграл (11.6.2) определяет массу этой поверхности (пусть ):

. (11.6.3)

Когда поверхность задана уравнением и она проектируется на плоскость Оху в область , то

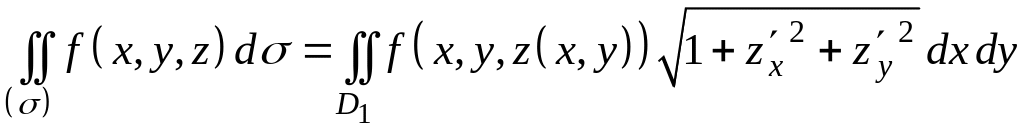, (11.6.4)

т. е. вычисление поверхностных интегралов сводится к вычислению двойных интегралов.

П ример 1. Вычислить поверхностный интеграл 1-го рода , где - конечная часть поверхности , отсеченная плоскостью .

Решение.

- параболоид вращения с ветвями парабол, направленных вниз, поднятый по оси Oz на 1. Проекцией рассматриваемой части параболоида (до плоскости ) на плоскость Оху является область, ограниченная окружностью . Следовательно, областью является круг .

Так как , , то

.

Для вычисления полученного двойного интеграла перейдем к полярным координатам , , , якобиан . , , .

.

Если поверхность задана уравнением, разрешенным относительно у; , то

, (11.6.5)

где - проекция поверхности на плоскость Oxz.

Если поверхность задана уравнением , то

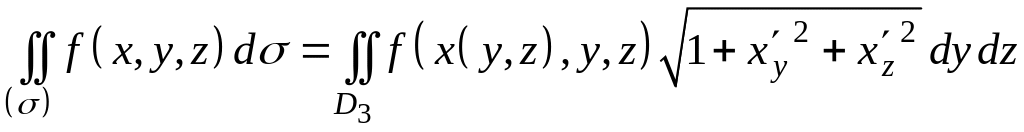, (11.6.6)

где - проекция поверхности на плоскость Oyz.

Если , то дает площадь поверхности .

В первом случае ( - уравнение )

. (11.6.7)

Аналогичные формулы получаются, если поверхность проецируется на другие плоскости координат.

Пример 2. Найти площадь поверхности сферы радиуса R.

Решение. Уравнение сферы .

, .

Тогда

.

.

Перейдем к полярным координатам .

,

а площадь всей поверхности сферы

.