11.2.2. Основные свойства тройного интеграла

1. .

2. , ( ).

3. , то .

4. Если во всех точках области функции и удовлетворяют соотношению , то

.

5. Если функция во всех точках области интегрирования удовлетворяет неравенствам , то

,

где V – объем области .

6. Тройной интеграл равен произведению значения подынтегральной функции в некоторой области интегрирования на объем области интегрирования, т. е.

.

Заметим, что если подынтегральная функция , то

, где V – объем области интегрирования .

11.2.3. Вычисление тройного интеграла в декартовых координатах

Вычисление тройного интеграла так же как и двойного, может быть осуществлено посредством ряда последовательных интегрирований.

Пусть дан тройной интеграл

,

причем область отнесена к системе декартовых координат Oxyz. Разобьем область интегрирования плоскостями, параллельными координатным плоскостям. Тогда частичными областями будут параллелепипеды с гранями, параллельными плоскостям Oxy, Oxz, Oyz. Элемент объема будет равен произведению дифференциалов переменных интегрирования

.

В соответствии с этим будем иметь:

.

Будем считать, что область имеет следующий вид.

Опишем около цилиндрическую поверхность с образующей, перпендикулярной к плоскости Оху. Она касается области вдоль некоторой линии L, которая делит поверхность, ограничивающую область на две части: верхнюю и нижнюю. Уравнение нижней поверхности пусть будет , а уравнение верхней .

Построенная цилиндрическая поверхность высекает из плоскости Оху плоскую область D, которая является ортогональной проекцией пространственной области на плоскость Оху; при этом линия L проектируется в границу области D.

Будем производить интегрирование сначала по направлению оси Oz. Для этого функция интегрируется по заключенному в отрезку прямой, параллельной оси Oz и проходящей через некоторую точку области D(отрезок ).

При данных х и у переменная интегрирования z будет изменяться от - аппликаты точки входа ( ) прямой в области , до - аппликаты точки выхода ( ) прямой из области .

Результат интегрирования представляет собой величину, зависящую от точки , обозначим ее через :

.

При интегрировании х и у рассматривают здесь как постоянные. Мы получим значение исходного тройного интеграла, если возьмем двойной интеграл от функции при условии, что точка изменяется по области D, т. е. . Т. о., тройной интеграл должен быть представлен в виде:

.

Приводя, далее, двойной интеграл по области D к повторному и интегрируя сначала по у, а затем по х, получим:

, (11.2.4)

где и - ординаты точек входа в область D и выхода из нее прямой (в плоскости Оху), а и b – абсциссы конечных точек интервала оси Ох, на которую проектируется область D.

Формула (11.2.4) сохраняется и для областей, имеющих цилиндрическую формулу, т. е. ограниченных цилиндрической поверхностью с образующими, параллельными оси Oz, а снизу и сверху поверхностями, уравнения которых соответственно и .

Если областью интегрирования служит внутренность параллелепипеда с гранями, параллельными координатным плоскостям, то пределы интегрирования постоянны во всех трех интегралах:

.

В этом случае интегрирование можно производить в любом порядке.

П ример. Вычислить , где область ограничена плоскостями , , , .

Решение. Нарисуем область . Это

треугольная пирамида.

Очевидно, что z изменяется от плоскости до наклонной плоскости . Тогда

.

11.3. Общая замена переменных в тройном интеграле.

Приложения кратных интегралов.

11.3.1. Общая замена переменных в тройном интеграле.

Пусть функции , , взаимнооднозначно отображают область в декартовых координатах x, y, z на область в криволинейных координатах t, u, v. Пусть элемент объема области переходит при этом в элемент объема области и пусть

.

Тогда

.

J называется якобианом, он вычисляется по следующей формуле:

11.3.2. Переход в тройном интеграле к цилиндрическим

координатам

Отнесем область к системе цилиндрических координат , в которой положение точки М в пространстве определяется полярными координатами ее проекции Р на плоскость Оху и ее аппликатой . Тогда

, , . (11.3.1)

Вычислим, чему равен якобиан J при переходе к цилиндрическим координатам:

.

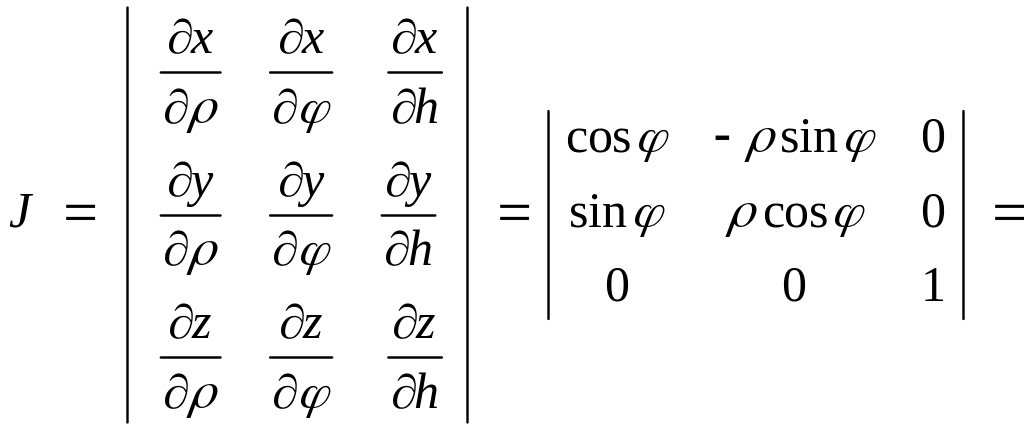
Замечание. При переходе к полярным координатам в двойном интеграле якобиан

.

Теперь . Т. о.

,

т. е., чтобы перейти в тройном интеграле к цилиндрическим координатам, нужно в выражении подынтегральной функции заменить x, y, z по формулам (11.3.1) и взять элемент объема равным . Если, в частности, , то интеграл выражает объем V области .

. (11.3.2)

Вычисление тройного интеграла в цилиндрических координатах приводится к интегрированию по , по и по h на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра , , то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:

.