11.3.3. Переход в тройном интеграле к сферическим координатам

Отнесем теперь область к системе сферических координат . В этой системе координат положение точки М в пространстве определяется ее расстоянием от начала координат (длина радиуса-вектора точки), углом между радиус-вектором точки и осью Oz и углом между проекцией радиуса-вектора точки на плоскость Оху с осью Ох.

При этом может изменяться от 0 до , а - от 0 до ( - долгота точки, - широта точки).

Установим связь между сферическими и декартовыми координатами. Из рисунка имеем:

, ,

, .

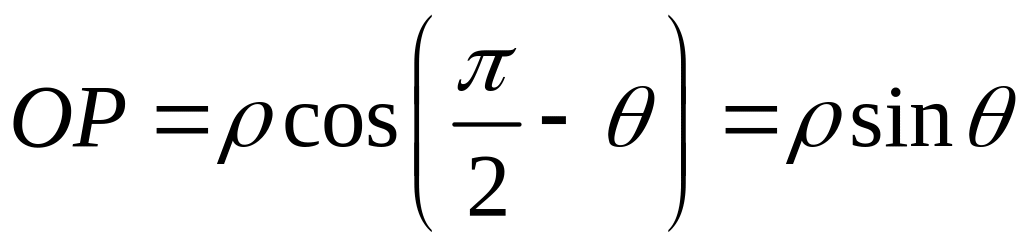Отсюда

(11.3.3)

Найдем якобиан при переходе в тройном интеграле к сферическим координатам.

.

.

. (11.3.4)

Заменив в тройном интеграле х, у, и z по формулам (11.3.3) и взяв элемент объема по формуле (11.3.4), будем иметь:

Особенно удобно применение сферических координат в случае, когда область интегрирования - шар с центром в начале координат или шаровое кольцо. Например, в последнем случае, если радиус внутреннего шара , а внутреннего , пределы интегрирования следует расставить так:

.

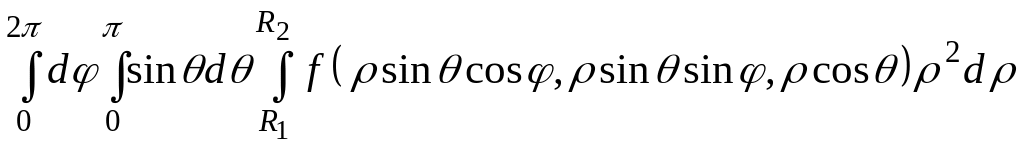Пример. Вычислить объем шара радиуса R.

Решение.

.

Отметим, что трудно дать общие указания, когда следует применять ту или иную систему координат. Это зависит и от области интегрирования, и от вида подынтегральной функции.

11.3.4. Приложения тройных интегралов

Объем тела

. (11.3.5)

Применение тройных интегралов к вычислению статических моментов и моментов инерции пространственных тел основано на тех же принципах, что и для двойного интеграла.

Для вычисления координат центра тяжести нужны статические моменты относительно координатных плоскостей Oxy, Oxz, Oyz; обозначим их соответственно , , . Легко получить следующие формулы для координат , , центра тяжести неоднородного тела, плотность которого задается функцией , занимающего область .

; ;

. (11.3.6)

Если тело однородное, т. е. , то формулы упрощаются:

; ; . (11.3.7)

Перейдем к вычислению моментов инерции тела относительно координатных осей. Т. к. квадраты расстояний от точки до осей Ox, Oy, Oz соответственно равны , , , то, полагая , получим:

, , . (11.3.8)

Аналогично плоскому случаю интегралы

, , (11.3.9)

называются центробежными моментами инерции.

- полярный момент инерции. (11.3.10)

11.4. Определение криволинейных интегралов 1-го и 2-го рода. Их основные свойства и вычисление.

11.4.1. Криволинейный интеграл по длине дуги (I рода).

Пусть функция непрерывна в некоторой области и L – линия целиком расположенная в этой области. Разобьем L на п участков; возьмем на каждом из участков произвольно точки и построим следующую интегральную сумму:

, (11.4.1)

где - длина соответствующего участка линии L.

О п р е д е л е н и е. Криволинейным интегралом по длине дуги называется предел п-й интегральной суммы (11.4.1) при условии, что длина наибольшего участка разбиения .

. (11.4.2)

Свойства криволинейного интеграла по длине совершенно аналогичны свойствам определенного интеграла. Вычисление их производится путем преобразования в обыкновенные определенные интегралы.

П р а в и л о. Для того, чтобы криволинейный интеграл , где линия L задана параметрическими уравнениями и , преобразовать в обыкновенный, нужно в подынтегральном выражении положить , , и взять интеграл по интервалу изменения t, соответствующему линии интегрирования:

. (11.4.3)

Если уравнение линии L задано в виде , , то положив , имеем:

. (11.4.4)

Если уравнение линии L - , , то положив , имеем:

. (11.4.5)

Пример 1. Вычислить , где L – дуга параболы от до . Здесь линию удобней задать в форме разрешенной относительно х:

, , .

.

З а м е ч а н и е 1.

- масса неоднородной линии L с заданной

поверхностной плотностью . (11.4.6)

Пример 2. Вычислить ,

где .

; .

.

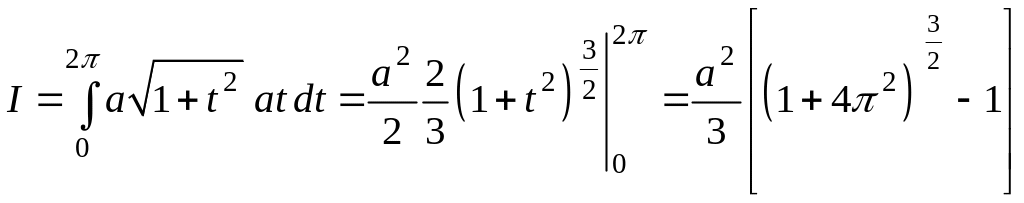З а м е ч а н и е 2. Если линия L расположена в пространстве и задана параметрически уравнениями: , , , то

. (11.4.7)