11.1.4. Двойной интеграл в полярных координатах
Для вычисления
двойного интеграла
мы пользовались до сих пор системой
декартовых координат. Отнесем теперь
плоскость к системе полярных координат
и
и предположим, как обычно, что полюс
лежит в начале координат и полярная ось
совпадает с осью абсцисс. Тогда
,
.
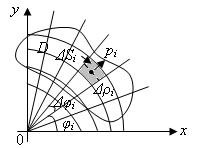
Разобьем область
интегрирования D
на частичные области двумя системами
координатных линий:
,
.
Этими линиями будут соответственно
концентрические окружности с центром
в полюсе и лучи, исходящие из полюса.
При этом частичными областями будут
криволинейные четырехугольники,
ограниченные дугами концентрических
окружностей и их радиусами. Площадь
будет
или
,
где
есть средний радиус между
и
.
Пусть дана функция
,
непрерывная в области D.
Составим для нее интегральную сумму,
разбивая область D
на частичные области и выбирая в качестве
произвольных точек
точки, лежащие на средних окружностях
радиуса
,
т. е. полагая
, 
.
Тогда
.
Так как в правой
части стоит интегральная сумма для
функции
по переменным
и
,
то переходя к пределу, получим:
. (11.1.7)
Это равенство
является формулой преобразования
двойного интеграла от декартовых
координат к полярным. Выражение
называется элементом площади в полярных
координатах.
Для того чтобы
преобразовать двойной интеграл в
декартовых координатах в двойной
интеграл в полярных координатах, нужно
х
и у
в подынтегральной функции заменить
соответственно через
и
,
а произведение
заменить произведением
.
Вычисление двойного интеграла в полярной системе координат так же как и в декартовой, сводится к последовательному интегрированию по переменным и . Укажем правила расстановки пределов.
1. Пусть полюс не
содержится внутри области интегрирования
D,
заключенной между лучами
и
,
и координатные линии
встречают ее границу не более чем в двух
точках.
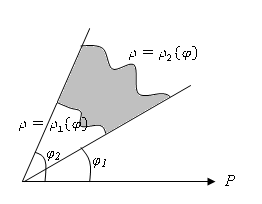
Полярные уравнения
кривых АЕС
и АВС
пусть будут
и
.
Интегрируя сначала
по
в пределах его изменения при постоянном
,
т. е. от
до
,
а затем по
от
до
,
получим:
.
Интегрирование в обратном порядке, т. е. сначала по , а потом по , обычно не встречается.
В частном случае,
когда областью интегрирования служит
часть кругового кольца
,
,
пределы интегрирования постоянны по
обеим переменным:
.
2. Пусть полюс содержится внутри области интегрирования и любой полярный радиус пересекает границу в одной точке (звездная область). Интегрируя сначала по , а затем по , получим:
,
где
есть уравнение границы области в полярных
координатах. В частности, при
,
т. е. когда область интегрирования есть
круг с центром в полюсе, будем иметь:
.
Пример
11.1.3.
Вычислить объем V
общей части шара радиуса а
и кругового цилиндра радиуса
при условии, что центр шара лежит на
поверхности цилиндра.
Решение.
Сверху цилиндрическое тело накрывает
сфера, уравнение которой
.
Имеем
,
где D – полукруг, являющийся половиной основания цилиндра. Здесь очень удобно перейти к полярным координатам. Имеем
.
Отсюда
.