11.1.5. Приложения двойных интегралов
1. Площадь области
интегрирования:
.
(11.1.8)
2. Объем цилиндрического тела: . (11.1.9)
3. Масса плоской пластинки переменной плотности.
Рассмотрим тонкую пластинку, расположенную на плоскости Оху и занимающую область D. Толщину этой пластинки считаем настолько малой, что изменением плотности по толщине ее можно пренебречь.
Поверхностной плотностью такой пластинки в данной точке называется предел отношения массы площадки к ее площади при условии, что площадка стягивается к данной точке.
Определенная таким образом поверхностная плотность будет зависеть только от положения данной точки, т. е. являться функцией ее координат:
.
Если
бы плотность была постоянной (
),
то масса всей пластинки равнялась бы
,
где S
– площадь пластинки. Найдем теперь
массу неоднородной пластинки, считая,
что ее плотность является заданной
функцией
.
Для этого разобьем область, занимаемую
пластинкой, на частичные области с
площадями
,
,
…,
.
Выбирая в каждой частичной области
произвольные точки
,
будем считать, что плотность во всех
точках частичной области постоянна и
равна плотности
в выбранной точке. Составим приближенное
выражение для массы пластинки в виде
интегральной суммы:
.
Для точного выражения массы следует найти предел суммы при условии, что и каждая частичная область стягивается к точке. Тогда
. (11.1.10)
4. Статические моменты и центр тяжести пластинки.
Статическим моментом материальной точки с массой т относительно какой-либо оси называется произведение массы на расстояние от точки до этой оси.
Вычислим сейчас статические моменты рассматриваемой пластинки относительно осей координат. Для этого сосредоточим в точках массы соответствующих частичных областей и найдем статические моменты полученной системы материальных точек относительно осей координат Ох и Оу.
, 
.
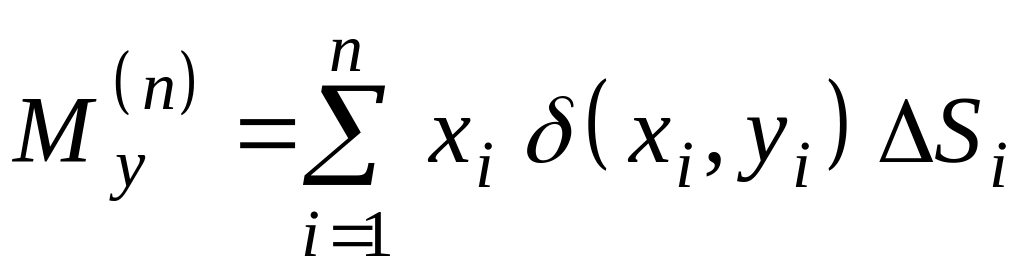Переходя к пределу при обычных условиях и заменяя интегральные суммы интегралами, получим:
, 
. (11.1.11)
Находим координаты
центра тяжести
.
, 
. (11.1.12)
Если пластинка
однородная, т. е.
,
то
, 
, (11.1.13)
где S – площадь пластинки.
5. Моменты инерции пластинки.
Моментом инерции материальной точки Р с массой т относительно какой-либо оси называется произведение массы на квадрат расстояния точки Р от этой оси.
Легко получить формулу:
, 
. (11.1.14)
Для однородной
пластинки (
):
, 
. (11.1.15)
Отметим, что двойной
интеграл
называется центробежным
моментом
инерции и обозначается
.
. (11.1.16)
В механике часто рассматривают полярный момент инерции точки, равный произведению массы точки на квадрат ее расстояния до данной точки – полюса.
. (11.1.17)
Вопрос вычисления площади поверхности пространственных тел с применением двойных интегралов будет рассмотрен на последней лекции данного учебного модуля.
11.2. Тройной интеграл. Вычисление тройного интеграла в декартовых координатах
11.2.1. Масса неоднородного тела. Определение тройного интеграла. Основные свойства тройного интеграла
Рассмотрим тело,
занимающее пространственную область
,
и предположим, что плотность распределения
массы в этом теле является непрерывной
функцией координат точек тела:
.
Единица измерения
плотности -
.
Разобьем тело
произвольным образом на п
частей; объемы этих частей обозначим
через
,
,
…,
.
Выберем затем в каждой части по
произвольной точке
.
Полагая, что в каждой частичной области плотность постоянна и равна ее значению в точке , мы получим приближенное выражение для массы тела в виде суммы:
. (11.2.1)
Предел этой суммы при условии, что и каждое частичное тело стягивается в точку и даст массу тела:
. (11.2.2)
Пусть
- произвольная непрерывная в области
функция. Составим для нее п-ю
интегральную сумму:
.
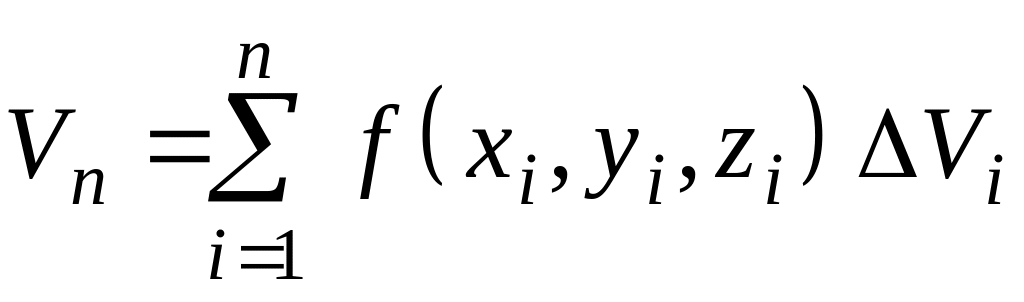По определению тройным интегралом назовем предел п-ой интегральной суммы, если и каждое частичное тело стягивается в точку.
Т. о.,
. (11.2.3)
Если непрерывна в области , ограниченной замкнутой поверхностью, то конечный предел существует, причем он не зависит от способа разбиения области на частичные и от выбора точек .