
- •Глава 3
- •3.1.1 Основные определения
- •3.1.2 Законы алгебры логики
- •Законы нулевого множества
- •Законы универсального множества
- •Законы двойной инверсии
- •9. Законы поглощения
- •11. Законы обобщенного склеивания
- •13. Теорема разложения
- •3.1.3 Элементарные логические функции и принцип двойственности
- •3.1.4 Классификация логических устройств и
- •Контрольные вопросы и задания
- •3.2.2 Представление логических функций (лф)
- •3.2.3 Понятие суперпозиции
- •Метод непосредственных преобразований
- •Метод Карно-Вейча
- •3.3.1 Метод непосредственных преобразований
- •3.3.2 Метод Карно-Вейча
- •Реализация логических функций
- •Особенности построения логических устройств
- •3.4.1 Реализация логических функций
- •3.4.2 Особенности построения логических устройств
3.3.2 Метод Карно-Вейча
Метод диаграмм Вейча (карт Карно) удобен для минимизации ЛФ, содержащих обычно не более пяти переменных.
Метод диаграмм Вейча, усовершенствованный Карно, применяется в том случае, если число аргументов не более 5. Представляют собой определенную таблицу истинности и отличаются друг от друга способом обозначения строк и столбцов таблицы истинности.
Число клеток карты Карно определяется величиной 2n, где п равняется числу входных переменных, с разметкой строк и столбцов переменными.
Например, если переменных 3 (n = 3), то (23 = 8) клеток -8.
Каждой комбинации переменных можно поставить в соответствие клетку карты Карно.
В клетку записывается значение функции (0 или 1) для данной комбинации входных переменных.
Входные переменные располагаются по внешним сторонам карты напротив ее строк и столбцов. При этом значение каждой из входных переменных относится ко всей строке или столбцу и равняется 1, если напротив строки (столбца) стоит под скобкой обозначение этой переменной; для других строк (столбцов) значение этой переменной равняется 0.
|
х2 |
2 |
х1 |
|
|
1 |
|
|
Диаграмма Вейча для двух переменных х1 и х2.
Переменных -2. Число клеток: 22 = 4
|
х2х3 |
х2 3 |
2 3 |
2х3 |
х1 |
|
|
|
|
1 |
|
|
|
|
Диаграмма Вейча для трех переменных х1, х2 и х3
Переменных -3. Число клеток: 23 = 8
|
х3х4 |
х3 4 |
3 4 |
3х4 |
х1х2 |
|
|
|
|
х1 2 |
|
|
|
|
1 2 |
|
|
|
|
1х2 |
|
|
|
|
Диаграмма Вейча для четырех переменных х1, х2 , х3 и х4
Переменных -4. Число клеток: 24 = 16
Каждая из входных переменных делит по-своему любую карту Карно на две равных части, в одной из которых значение этой переменной равняется 1, а в другой 0.
Для минимизации логическая функция (ЛФ) приводится к совершенной дизъюнктивной нормальной форме (СДНФ), после чего заполняется диаграмма для п переменных. При этом в соответствующую клетку диаграммы вписывается 1, если ЛФ = 1 в данном наборе. В остальные клетки вписываются 0 либо эти клетки вообще не заполняются.
В заполненной диаграмме обводят прямоугольными контурами клетки с 1, после чего записывают минимизированную дизъюнктивную нормальную форму (МДНФ) логической функции в виде дизъюнкции простых импликант, описывающих эти контуры.
При проведении контуров придерживаются следующих правил:
-количество клеток с 1 должно выражаться величиной 2i, где i = 0, 1, 2, … (т.е. 1, 2, 4, 8 и т.д.);
-1 в крайних клетках одного столбца или одной строки могут включаться в один контур;
-каждый контур должен включать как можно большее число клеток с 1, а общее число контуров должно быть как можно меньшим.
В простую импликанту, описывающую контур, включаются те переменные, которые во всех клетках контура имеют либо только прямое, либо только инверсное значение.
Пример
1.
Минимизировать ЛФ F
=![]() х2
+
х1
х2
+
х1![]() +
1
+
1![]() с
помощью диаграмм Вейча.
с
помощью диаграмм Вейча.
Заполняем диаграмму Вейча для двух переменных.х2
2
х1
0
1
1
1
1
Проводим два контура, охватывающие клетки с единицами.х2
2
х1
0
 1
11
1

1
Находим простые импликанты описывающие контур, для чего выясняем от каких переменных не зависит данный контур.
а)
вертикальный
контур охватывает строки с х1
и ![]() 1,
следовательно в простую импликанту,
описывающую горизонтальный
контур х1
входить не будет.
1,
следовательно в простую импликанту,
описывающую горизонтальный
контур х1
входить не будет.
б) горизонтальный контур охватывает строки с х2 и 2, следовательно в простую импликанту, описывающую вертикальный контур х2 входить не будет.
4. Следовательно, ЛФ будет иметь МДНФ: F = 1 + 2.
Пример
2. Минимизировать
ЛФ F=х1х2+х1![]() х3+
1
х3+
1х2
х3+
1
х3+
1х2![]() с
помощью диаграмм Вейча.
с
помощью диаграмм Вейча.
Приводим логическую функцию к СДНФ:
F = х1х2 (х3+ ) + х1 х3+ 1 х3 + 1х2 = х1х2х3 + х1х2 + х1 х3+ 1 х3 + 1х2
Заполняем диаграмму Вейча для трех переменных.х2х3
х2 3
2 3
2х3
х1
1
1
0
1
 1
10
1
0
1
Проводим три контура, охватывающие клетки с 1.х2х3
х2 3
2 3
2х3
 х1
х11
1

0

1
1
0
1
0
1
1 контур (зеленый) –охватывает клетки х1х2х3 и х1 х3
2 контур (красный)
–охватывает клетки х1х2![]() 1
х3
1
х3
3
контур
(красный) –охватывает клетки х1
х3![]() 1
х3
1
х3
Находим простые импликанты описывающие контур, для чего выясняем от каких переменных не зависит данный контур.
Для 1 контура это -
х1х
Для 2 контура это -
х2
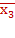
Для 3 контура это -
 х3
х3Следовательно, ЛФ будет иметь МДНФ: F = х1х3 + х2 +
 х3
х3
В
этом примере вместо 1 контура можно было
провести контур охватывающий конъюнкции
х1х2х3
и х1х2![]() ,
тогда
МДНФ
имела бы вид:
F
= х1х2
+ х2
+
х3
. Таким
образом, для этой функции возможны две
тупиковые
формы, равноценные по числу букв и
слагаемых, и каждую из них можно выбрать
для построения комбинационной схемы.
,
тогда
МДНФ
имела бы вид:
F
= х1х2
+ х2
+
х3
. Таким
образом, для этой функции возможны две
тупиковые
формы, равноценные по числу букв и
слагаемых, и каждую из них можно выбрать
для построения комбинационной схемы.
Карты Карно
Для минимизации функции с числом переменных n ≤ 6 используют карты Карно.
Число клеток карты Карно определяется величиной 2n, где п равняется числу входных переменных, с разметкой строк и столбцов переменными.
Например, если переменных 3 (n = 3), то (23 = 8) значит клеток -8.
Карты Карно для функции трех переменных F(х1 х2, х3) показаны на рис. 3.10.
Строки карты отмечены значениями переменной х1, а столбцы -значениями переменных х2, х3.
Каждая клетка карты Карно однозначно соответствует одному набору таблицы истинности для функции трех переменных (рис. 3.10, а) или минтермам этой функции (рис. 3.10, б).
Клетки карты Карно часто нумеруют десятичными цифрами - номерами наборов (рис. 3.10, в).
П
 ри
минимизации для каждого минтерма,
входящего в СДНФ функции, ставится
единица, а другие клетки не заполняются.
ри
минимизации для каждого минтерма,
входящего в СДНФ функции, ставится
единица, а другие клетки не заполняются.
Рисунок 3.10 – Карты Карно для функций трех переменных
Например, заполнение карты Карно для функции, заданной табл. 3.12, показано на рис. 3.6, г.
Таблица 3.12 - Функции трех переменных Р(X1 X2 X3) |
||||
№ строки |
X1 |
Х2 |
X3 |
P |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
1 |
3 |
0 |
1 |
0 |
0 |
4 |
0 |
1 |
1 |
1 |
5 |
1 |
0 |
0 |
1 |
6 |
1 |
0 |
1 |
0 |
7 |
1 |
1 |
0 |
1 |
8 |
1 |
1 |
1 |
1 |
Минтермы в соседних клетках карты Карно в строке (включая верхние и нижние) или в столбце (включая крайние) отличаются значением одной переменной, что позволяет выполнить операцию склеивания по этой переменной.
Например,
на
рис.
3.6, г
минтермы
![]()
![]() X3
и
X3
и
![]() Х2
Х3
(клетки
с
номерами
1
и
3) отличаются
значением
переменной
Х2,
поэтому
они
склеиваются
по
ней
и
представляются
конъюнкцией
двух
переменных
Х3.
Х2
Х3
(клетки
с
номерами
1
и
3) отличаются
значением
переменной
Х2,
поэтому
они
склеиваются
по
ней
и
представляются
конъюнкцией
двух
переменных
Х3.
Аналогично
для
минтермов
Х1
![]() и
Х1
Х2
(номера
клеток
4 и
6) склеивание
происходит
по
переменной
Х2
и
получают
конъюнкцию
Х1
.
и
Х1
Х2
(номера
клеток
4 и
6) склеивание
происходит
по
переменной
Х2
и
получают
конъюнкцию
Х1
.
В результате минимизации функции Р(Х1 Х2, Х3) получают ее минимальное выражение
Р
= ![]() Х3
v
Х2
Х3
v
Х1
Х3
v
Х2
Х3
v
Х1
![]() .
.
Перечислим общие правила минимизации.
Изображают карту Карно для n переменных и производят разметку ее строк и столбцов. В клетки таблицы, соответствующие минтермам (единичным наборам) минимизируемой функции, записывают единицу.
Склеиванию подлежат прямоугольные конфигурации, заполненные единицами и содержащие 2, 4 или 8 клеток. Верхние и нижние строки, крайние левые и правые столбцы карты как бы склеиваются, образуя поверхность цилиндра.
Множество прямоугольников, покрывающих все единицы, называется покрытием. Чем меньше прямоугольников и чем больше клеток в прямоугольниках, тем лучше покрытие.
Из
нескольких
вариантов
выбирают
тот,
у
которого
меньше
коэффициент
покрытия
z
= ![]()
где r — общее число прямоугольников,
s — их суммарная площадь в клетках.
Например, для изображенного покрытия (рис. 3.6,г) имеем z = 3/5.
Формулы, полученные в результате минимизации, содержат r элементарных конъюнкций (по числу прямоугольников в покрытии). Каждая конъюнкция содержит только те переменные, которые не меняют своего значения в склеиваемых наборах в соответствующем прямоугольнике.
Число переменных в конъюнкции называется ее рангом.
При склеивании двух соседних клеток получают ранг конъюнкции n-1, четырех клеток — n-2 , восьми клеток — n-3 и т.д.
Разметка карт Карно для функций четырех переменных показана на рис. 3.11.

Рисунок 3.11 – Карты Карно для функции 4 переменных:
а) двоичное значение минтермов; б) десятичное значение минтермов
В клетки карт записаны значения минтермов в двоичных и десятичных эквивалентах.
Пример. Минимизировать булевы функции L1 , L2 и L3 четырёх переменных.
Функция
L1
задана двумя способами – в СДНФ и с
десятичными эквивалентами минтермов: L1
=
![]()
![]() v
Х4
v
Х3
v
v
Х4
v
Х3
v
![]() Х4
Х4
![]()
![]() v
v
v
![]() v
Х1
Х2
v
X1
X2
X3
Х4
= 0
v
Х1
Х2
v
X1
X2
X3
Х4
= 0 ![]() 1
2
3
4
8
12
15
1
2
3
4
8
12
15
Функции L2 и L3 для упрощения заданы десятичными эквивалентами минтермов:
L2
= 2
3![]() 6
7
8
9
12
13; L3
= 1
3
5
7
9
11
13
15.
6
7
8
9
12
13; L3
= 1
3
5
7
9
11
13
15.
Минимизация функций производится на основе карт Карно (рис. 3.12).
Результаты минимизации:

L1 L2 L3
Рисунок 3.12-Карты Карно для минимизации функций четырёх переменных: L1 , L2 и L3
Результат
минимизации: L1
=
v
v
X1
X2
X3
Х4; z
=
![]() ;
;
L2
=
Х3
v
; z
=
![]() ;
;
L3
= Х4
; z
=
![]() .
.
Контрольные вопросы и задания
В чем заключаются цель и принципы минимизации логических устройств?
В чем заключается минимизация функции алгебры логики (ФАЛ) методом непосредствен-ных преобразований?
В чем заключается минимизация ФАЛ с помощью карт Карно—Вейча?
Приведите свойства карт Карно—Вейча.
Представьте карты Карно—Вейча функции трех, четырех и пяти переменных.
В чем заключается минимизация не полностью определенной ФАЛ?
К чему сводится алгоритм минимизации ФАЛ методом Квайна и Мак-Класки?
Что такое импликанта и покрытие Квайна?
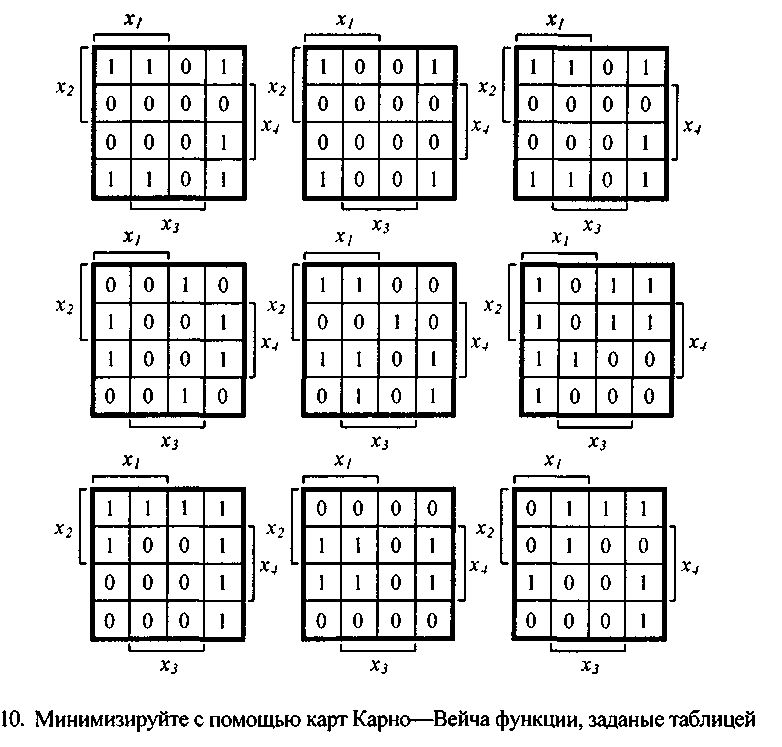 Минимизируйте
функции,
заданные
в
табличной
форме,
по
единичному
значению
функции.
Минимизируйте
функции,
заданные
в
табличной
форме,
по
единичному
значению
функции.
Образуйте СДНФ и СКНФ функции, заданной таблицей
Х3 |
Х2 |
Х1 |
F(x) |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |

