63

Основы теории компьютерной схемотехники

К олесников Л.П.

Глава 3

ФПТ 2009

СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ

Бабич Н.П., Жуков И.А. Компьютерная схемотехника. – Киев. МК-Пресс, 2004 -576 с.

А.В.Кузин, М.А.Жаворонков. Микропроцессорная техника. Учебник – М. Академия, 2006 -301 с.

Г.Р. Грейнер и др. Проектирование бесконтактных управляющих логических устройств промышленной автоматики. М. Энергия 1977. -378 с.

А.Н.Морозевич и др. МикроЭВМ, микропроцессоры и основы программирования. Минск. Высшая школа, 1990 – 348 с.

Н.П.Сергеев, Н.П.Башкевич. Основы вычислительной техники. Учебное пособие для ВУЗов – М. Высшая школа, 1988 – 308 с.

3.1.1 Основные определения

3.1.2 Законы алгебры логики

3.1.3 Элементарные логические функции и принцип двойственности

3.1.4 Классификация логических устройств и основные сведения о дискретных автоматах

3.1.1 Основные определения

Теоретической основой компьютерной схемотехники является алгебра логи­ки — наука, которая использует математические методы для решения логических задач. Алгебру логики называют булевой в честь английского математика Дж. Буля, внесшего наибольший вклад в развитие этой науки.

Основным предметом булевой алгебры является высказывание — простое предложение, о котором можно утверждать: истинно оно (обозначают символом 1) или ложно (обозначают символом 0).

Обычно простые высказывания обозначают малыми буквами латинского алфавита, например, х₁ х₂, ..., х_n, или a, b, c, … z, которые в компьютерной схемотехнике называют переменными (аргументами).

С помощью логических связок НЕ, ИЛИ, И, ЕСЛИ... ТО... строят сложные высказывания, которые называют булевыми (логическими) функциями и обозначают большими буквами латинского алфавита А, F, L, К, М, Р и др.

В настоящее время главная задача алгебры логики — анализ, синтез и струк­турное моделирование любых дискретных конечных систем. Аппарат булевой ал­гебры распространяется на объекты самой различной природы безотносительно их сути, лишь бы они характеризовались двумя значениями или состояниями: контакт включен или выключен, наличие высокого или низкого уровня электрического напря­жения, выполнение или невыполнение некоторого условия работы и т.д.

Использование аппарата алгебры логики в компьютерной схемотехнике осно­вано на том, что цифровые элементы характеризуются двумя состояниями, в общем случае это константы 0 и 1, и благо­даря этому могут быть описаны булевыми функциями.

Стандарт ДСТУ 2533-94 "Арифметические и логические операции. Термины и определения" конкретизировал основные понятия булевой алгебры в системах обработки информации.

Переменную с конечным числом значений (состояний) называют переключа­тельной, а с двумя состояниями — булевой.

Функция, которая имеет, как и каждая ее переменная, конечное число значений, называется переключательной (логиче­ской).

Л огическая функция, число возможных значений которой и каждой ее незави­симой переменой равно двум, является булевой.

Таким образом, булева функция — это частный случай переключательной (логической).

Операция — это четко определенное действие над одним или несколькими операндами, которое создает новый объект (результат). В булевой операции опе­ранды и результат принимают "булево значение 1" (далее просто значение 1) и "бу­лево значение 0" (далее просто значение 0). Булеву операцию над одним операн­дом называют одноместной, над двумя — двуместной и т.д.

Булевы функции могут зависеть от одной, двух и в целом от п переменных.

За­пись F {X₁, X₂, ... ,X_n) означает, что некоторая булева функция F зависит от перемен­ных Х₁, Х₂,...,Х„.

Основными булевыми операциями являются отрицание (операция НЕ, инверсия), дизъюнкция (операция ИЛИ, логическое сложение, объединение) и конъюнкция (операция И, логическое умножение).

Отрицание — это одноместная булева операция F = (читается "не X'), ре­зультатом которой является значение, противоположное значению операнда.

Дизъюнкция (от анг. –разъединение)— это булева операция F = Х₁ + X₂ (читается "Х₁ или Х₂"), резуль­татом которой является значение нуль тогда и только тогда, когда оба операнда имеют значение нуль. Часто исполь­зуют запись Х v Х₂ или Х₁ Х₂

Конъюнкция (от анг. –соединение)— это булева операция F = Х1 ∙ Х2 (читается "Х₁ и Х₂"), результа­том которой является значение единица тогда и только тогда, когда значение каждо­го операнда равно единице. В выражении Х₁∙ Х₂ точку можно опускать, часто исполь­зуют запись Х₁ Х₂ , Х₁ Х₂ или Х₁ & Х₂.

Операции отрицания, дизъюнкции и конъюнкции можно задать с помощью таб­лиц истинности (табл. 3.1, 3.2 и 3.3), в которых слева представлены значения операн­дов, а справа — значения булевой функции.

Табл. 3.1 –Операция отрицания Табл. 3.2 –Операция дизъюнкции Табл. 3.3 –Операция конъюнкции

X	F =		X1	X2	F = X1 + X2		X1	X2	F = X1 ∙ X2
0	1		0	0	0		0	0	0
1	0		0	1	1		0	1	0
			1	0	1		1	0	0
			1	1	1		1	1	1

В таблицах булевы функции ИЛИ, И заданы для двух переменных Х₁, Х₂, а можно и для нескольких X₁, X₂, Х₃ ... ,X_n

Областью определения булевой функции F (X₁, X₂,...,Х_n) является конечное множество различных двоичных наборов длиной п, на каждом из которых указыва­ется значение функции нуль или единица. Количество разнообразных двоичных на­боров равно множеству n-разрядных двоичных чисел m = 2ⁿ.

Например, для функ­ции двух переменных Х₁ и Х₂ имеется четыре двоичных набора:

< 0,0 >; < 0,1 >; <1,0>; <1,1>.

Часто наборы нумеруются десятичными эквивалентами двоичных чисел от ну­ля до 2ⁿ - 1. Например, для п = 4, наборы < 0101 > и < 1001 > имеют соответ­ственно номера 5 и 9.

Две функции отличаются одна от другой, если их значения будут разными, хотя бы в одном наборе. Число различных булевых функций от n пе­ременных равно 2^m, где m = 2ⁿ.

Одной из интерпретаций булевых операций являются схемы, состоящие из ключей, источника напряжения Е и лампочки Л. Для реализации операции дизъ­юнкции двух переменных Х₁ и Х₂ используют два параллельно соединенных нор­мально разомкнутых ключа (рис. 3.4, а).

При нажатии любого ключа (X₁ = 1 или Х₂ = 1) или обеих вместе лампочка горит (значение 1). Для реализации операции конъюнкции двух переменных X1 и Х2 приме­няют два последовательно соединенных нормально разомкнутых ключа (рис. 3.4, б). При нажатии одновременно обоих ключей (Х₁ =Х₂ = 1) лампочка горит (значение 1).

Для реализации операции отрицания применяют нормально замкнутый ключ (рис. 3.4, в). При Х = О ключ замкнут, и лампочка горит; при Х= 1 ключ размыкается, и лампочка не горит.

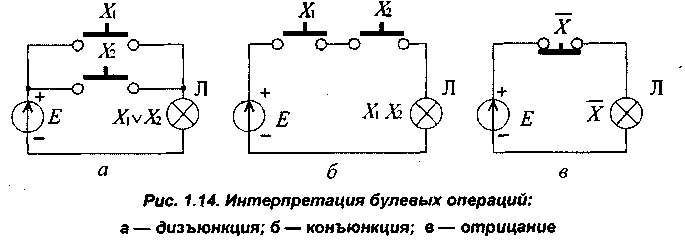
Рисунок 3.4 – Интерпретация булевых операций: а –дизъюнкция; б – конъюнкция; в - отрицание

Произвольную булеву функцию можно задать разными способами:

• словесным описанием,

• временными диаграммами,

• геометрическими фигурами,

• графами,

• таб­лицами истинности

• аналитическими выражениями.

Словесное описание функций наиболее часто применяется для первичного, начального описания поведения логического устройства.

Пример 3.1: Логическая функция трех переменных равняется единицы, если хотя бы две входные переменные равняются единицы.

Пример 3.2: Словесное описание некоторой булевой функции F{X₁ X₂) можно представить и так: F = 1, когда Х₁Х₂ = 1 и F = 0, если Х₁ Х₂ = 0.

Временная диаграмма функции представлена на рис. 3.1, а

Геометрически с помощью двухмерного ку­ба (рис.3.1,б), в котором точками выделены единичные вершины (данная функция принимает значение единицы на наборе 11).

Графом, где вершины ото­бражают значение нуля и единицы, а на ориентированных дугах переменные указыва­ют условия переходов (рис. 3.1, в).

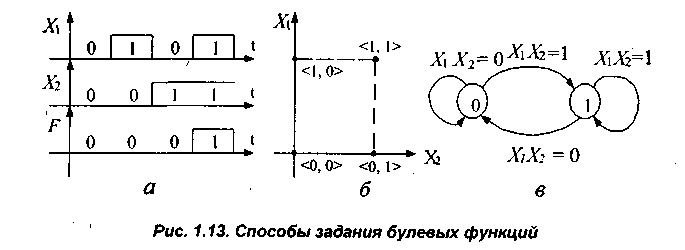
Рисунок 3.1 – Способы задания булевых функций

Таблицы истинности. Таблица, которая содержит все возможные комбинации входных переменных X_n-1, . . . X₂, Х₁, X₀ и соответствующие им значения выходных переменных Y_i , называется таблицей истинности или комбинационной таблицей.

В общем случае таблица истинности содержит 2ⁿ строк, где n –число переменных.

Если n = 2 (2² =4) -число строк -4, для n = 3 (2³ =8) -число строк -8 и т.д.

Таблица 3.4 – таблица истинности логической функции 3-х переменных (для примера 3.1)

х1	х2	х3	F(x1, x2, x3)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Чтобы построить таблицу, нужно вычислить значение функции F(x₁, x₂, x₃) для каждой из восьми комбинаций значений входных переменных. Так например, для первой строчки таблицы, при х₁ =0, х₂ =0, х₃ =0 F(0,0,0) = 0∙0∙0 + (0+0)∙(0+1) = 0

По таблице истинности можно составить алгебраическое выражение. При этом запись алгебраического выражения осуществляется с использованием совершенной дизъюнктивной нормальной формы (СДНФ), которую рассмотрим чуть позже (гл.3.4).

Аналитическое (алгебраическое) выражение или булево выражение, представляет собой формулу, состоящую из логических переменных, связанными операциями И, ИЛИ, и НЕ.

Пример 3.3: F(x₁, x₂, x₃) = х₁ х₂ х₃ + (х₁ + х₂)( х₁ + ₃)

Как и в обычных алгебраических выражениях для задания порядка действий используются скобки. Предполагается, что выполнение операции И предшествует операции ИЛИ.

Вопросы для самопроверки

1. Что такое алгебра логики и какая её главная задача.

2. Что такое высказывание и как обозначаются простые и сложные высказывания.

3. С чем связано использование аппарата алгебры логики в компьютерной схемотехнике.

4. Что такое логическая функция.

5. Что такое операция.

6. Какие булевы операции являются основными.

7. Как можно задать с помощью таб­лиц истинности операции И, ИЛИ, НЕ.

8. Произвольную булеву функцию можно задать разными способами, какими?

9. Приведите пример словесного описания функции.

10. Приведите пример алгебраического описания функции.