3.3.1 Метод непосредственных преобразований

Одним из простейших методов минимизации является метод непосредственных преобразований, который применяется с использованием основных теорем алгебры логики.

Важные теоремы, отражающие основные соотношения алгебры логики (Табл. 3.9)
1	x + 0 = x	x ∙ 1 = x
2	x + 1 = 1	x ∙ 0 = 0
3	x + x = x	x ∙ x = x
4	x + = 1	x ∙ = 0
5	= x	-
6	x + y = y + x	x ∙ y = y ∙ x
7	x + x ∙ y = x	x (x + y) = x
8	x + (y + z) = (x + y) + z	x (y ∙ z) = (x ∙ y) z
9	x + y ∙ z = (x + y) (x + z)	x (y + z) = x ∙ y + x ∙ z
10	= ∙	x ∙ y = x + y
11	(x + y) ( + y) = y	(x ∙ y) +( ∙ y) = y

Непосредственное упрощение исходной логической функции, заданной в виде СДНФ, выполняется в следующем порядке:

1. Для каждой из возможных пар соседних конституант СДНФ применяется операция полного склеивания. При этом из них исключается по одной пе­ременной. Потом выполняется приведение подобных членов. Этот процесс повторяется до тех пор, пока в полученном выражении не останется конъюнкций, которые отличаются друг от друга значениями одной пере­менной. Полученная таким способом форма называется сокращенной нормальной формой. Конъюнкции, которые входят в сокращенную нор­мальную форму, называются простыми импликантами. Каждой логиче­ской функции отвечает лишь одна сокращенная форма.

2. Применяя к сокращенной нормальной форме операцию обобщенного склеивания, исключают из нее лишние конъюнкции (импликанты). Полу­ченная в результате последовательного ряда таких преобразований форма, не допускающая дальнейших склеиваний, называется тупиковой формой логической функции. Тупиковых форм для одной функции может быть несколько.

3. Полученная тупиковая форма может случайно оказаться минимальной. Минимальной формой является тупиковая форма минимальной длины. В общем случае для поиска минимальной формы необходим перебор ту­пиковых форм, который позволяет найти одну или несколько минималь­ных форм логической функции.

Метод Квайна применяется к функциям, задан­ным в СДНФ (возможно задание и в СКНФ), и проводится, как правило, в два этапа.

На первом этапе выполняется переход от СДНФ к сокращенной ДНФ путем проведения всех возможных склеиваний друг с другом сначала конъюнкций ранга п, затем ранга п — 1, далее п — 2 и т. д. Каждый раз в группе конъюнкций отыскиваются пары конъюнкций вида Ах и А , где А — общая часть этих конъюнкций. Эти конъюнкции склеиваются между собой по переменной х

Например, конъюнкции _{1 2}х_{3 4}, и ₁х₂х_{3 4} имеют общую часть А = ₁х_{3 4} и склеиваются по переменной х₂. В результате склеивания получим из конъюнкций ранга п=4, конъюнкции ₁х_{3 4}, и ₁х_{3 4} ранга п - 1 = 3.

При этом получается конъюнкция А ранга п-1, а конъюнкции Ах и А помечаются и срав­ниваются также со всеми другими конъюнкциями ранга п с целью выполнения операции склеивания.

Результатом выполнения последовательности попарного сравнения и склеивания конъюнкций ранга п является группа конъюнкций ранга п —1 и непомеченные конъюнкции ранга г. Непомеченные конъюнкции ранга п не участ­вовали в склеивании, следовательно, являются простыми импликантами и включаются в сокращенную ДНФ.

Конъюнкции ранга п—1 вновь подвергаются попарному сравнению и склеиванию, как это было описано выше для конъюнкций ранга п; в результате имеем группу конъюнкций ранга п—2 и непомеченные конъюнкции ранга п—1, которые являются простыми импликантами, включаемыми далее в сокращенную ДНФ.

Первый этап заканчивается тогда, когда вновь полученная группа конъюнкций не содержит склеивающихся членов, т. е. содержит только простые импликанты. После этого запи­сывается сокращенная ДНФ, в которую включаются все полученные простые импликанты.

Рассмотрим реализацию первого этапа на примере функции ЛФ f

1 2 3 4 5

f = + + + + (3.5)

где для удобства последующего изложения над конъюнк­циями записаны присвоенные им номера.

Анализируя в выражении всевозможные пары конъюнкций 1-2, 1-3, 1-4, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5, 4-5, находим, что операция склеивания выпол­няется между парами 1-3 по х₁, 2-5 по х₁, 3-4 по х₃, 4-5 по х₂.

Таким образом, все конъюнкции исходной СДНФ участвуют в склеивании и помечаются подчеркиванием. 1 2 3 4

Теперь исходная СДНФ (3.5) записывается в виде f = _{2 3} + х₂х₃ + х_{1 2} + х₁x₃. (3.6)

Продолжая для выражения (3.6) процедуру склеивания, сравниваем попарно конъюнкции 1-2, 1-3, 1-4, 2-3, 2-4 и 3-4. Эти пары конъюнкций между собой не скле­иваются. Поэтому полученная запись ЛФ (3.6) представ­ляет собой сокращенную ДНФ исходной ЛФ (3.5), содер­жащей только простые импликанты.

Второй этап заключается в переходе от сокращенной ДНФ к тупиковым ДНФ и выборе среди них МДНФ.

Тупиковой называется такая ДНФ, среди простых импликант которой нет ни одной лишней. При этом под лишней понимается такая простая импликанта, удаление которой не влияет на значение истинности этой функции.

Воз­можны случаи, когда в сокращенной форме нет лишних простых импликант. Тогда сокращенная ДНФ является тупиковой.

Для выявления лишних простых импликант строится импликантная матрица, которая называется также матри­цей (таблицей) покрытий. Каждая строка импликантной матрицы соответствует одной простой импликанте, а столбцы — конституантам единицы, которыми они и помечаются. Для рассматриваемого примера импли­кантная матрица приведена в табл. 3.14.

Таблица 3.14 - Импликационная матрица для выражения 3.5
№	Простые импликанты	Конституанты единиц
1	2 3	+		+
2	х2 х3		+				+
3	х1 2			+	+
4	х1 x3			+	+		+

Нахождение тупиковых ДНФ по импликантой матри­це начинается с разметки матрицы. При этом каждая импликанта сравнивается со всеми конституантами еди­ницы. Если импликанта является собственной частью некоторой конституанты, то на пересечении строки и столбца ставится условный знак, например – плюс (+).

Кон­ституенты единицы, помеченные в строке с простой импликантой, поглощаются (покрываются) этой простой импликантой. Это значит, что на соответствующих набо­рах данная импликанта обеспечивает единичные значе­ния ЛФ.

Например, простая импликанта _{2 3} входящая в сокращенную ДНФ (3.6) рассматриваемого примера, является собственной частью конституант единиц и , и поэтому в строке с данной простой импли­кантой (табл. 3.13) поставлены две пометки X в соответ­ствующих колонках. Аналогично размечены другие стро­ки табл. 3.13.

Выявление лишних простых импликант выполняется следующим образом:

-В импликантной таблице условно вычеркивается строка с проверяемой простой импликан­той вместе с соответствующими пометками в строке.

-Если при этом окажется, что в каждом столбце импли­кантной таблицы остается, хотя бы по одной пометке, проверяемая импликанта является лишней и ее следует удалить.

-Оставшиеся простые импликанты покрывают все единичные значения ЛФ.

-Испытание каждой последую­щей простой импликанты возможно лишь после удаления уже выявленных лишних простых импликант.

-Изменение последовательности испытаний и удаления лишних членов сокращенной ДНФ может привести к различным тупико­вым формам ЛФ, из которых выбирается МДНФ.

Из табл. 3.13 видно, что только простая импликанта 1 обеспечивает единичное значение ЛФ на наборе 000, а импликанта 2 — на наборе 011 (соответствующие этим наборам столбцы обозначены конституантами единицы и ), поэтому эти простые импликанты обя­зательно войдут во все тупиковые ДНФ.

Простую импликанту 3 можно считать лишней. Однако, если ее сохра­нить, лишней можно считать простую импликанту 4.

Таким образом, для ЛФ возможны две тупиковые формы:

f_1т = _{2 3} + х₂х₃ + х₁x₃ , (3.7)

в которую не включена лишняя импликанта х_{1 2}

и f_2т = _{2 3} + х₂х₃ + х_{1 2} , (3.8)

в которую не вошла лишняя импликанта x₁x₃.

Тупиковые формы (3.7) и (3.8) имеют одинаковое суммарное количество переменных, поэтому любую из них можно выбрать в качестве минимальной (МДНФ).

Например, можно считать f_min = f_1т = _{2 3} + х₂х₃ + х₁ x₃ .

Эта ЛФ реализует­ся схемой с ценой С = 9 (3 х 2 + 3 = 9).

Пример 4. Логическую функцию F в виде СДНФ F = х₂ +х₁ +х₁ х₃+х₁х₂ +x₁x₂x₃ можно минимизировать следующим образом:

1. Добавим к данной функции слагаемое х₁х₂ , которое уже есть в данной функции, используя правило 3 (x ∙ x = x).

F = х₂ + х₁ + х₁ х₃ +х₁х₂ + x₁x₂x₃ + х₁х₂

2. Применим метод склеивания (правило 11) к одинаково подчеркнутым элементарным конъюнкциям (x ∙ y + ∙ y = y):

Для х₁ и х₁ х₃ по х₃ -получим х₁

Для х₂ и х₁х₂ х₁ -получим х₂ ;

Для х₁х₂ и x₁x₂x₃ по х₃ -получим x₁x₂.

Результат склеивания: F = х₂ + х₁ + x₁x₂

3. Применим тот же метод склеивания для двух последних элементарных конъюнкций:

Для х₁ и x₁x₂ по х₂ -получим х₁

Окончательный результат: Fmin =F_T = х₂ + x₁

Полученная в результате минимизации логическая функция называется тупиковой. Логическая функция может иметь несколько тупиковых форм.

Пример5. Найти минимальную форму функции, заданной СДНФ

F(a, b,c) =а c + c + + + ab = abc.

Применяя операцию полного склеивания к сочетаниям каждой конституанты со всеми соседними и приводя подобные члены, получаем сокращенную нормальную форму:

F(a,b,c) = + c + ac + ab + b + .

П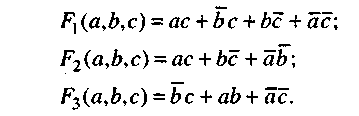 рименение операции обобщенного склеивания к импликантам можно осу­ществить в нескольких вариантах. Каждому из них отвечает одна из следующих тупиковых форм:

Очевидно, что анализируемой функции отвечают две минимальных нормаль­ных формы F₂(a,b,c) и F₃{a,b,c).

Для исходной функции, заданной в виде СКНФ, минимизация методом непо­средственного упрощения выполняется таким образом.

1. Сначала к членам СКНФ применяют операцию полного склеивания.

2. Пользуясь законом дистрибутивности, раскрывают скобки в полученном выражении.

3. Приводят подобные члены и применяют операцию поглощения.

4. Полученную таким способом ДНФ минимизируют в указанном выше по­рядке.