МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное учреждение

высшего профессионального образования

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ

Экономический институт

Кафедра экономического анализа и статистики

АНАЛИЗ РИСКА

Методические указания

Новосибирск 2010

УДК 336.7(075)

ББК 65.261 Б74

Анализ риска: Методические указания для практических занятий/ Новосиб. гос. аграр. ун-т. Экон. ин-т;

Сост. к.э.н., доцент С.А. Шелковников. – Новосибирск, 2010. - 24 с.

В методических указаниях дается системное представление о риске в рыночной экономике с целью сформировать у студентов глубокие знания сущности методов анализа и снижения экономических рисков хозяйствующих субъектов.

Методические указания предназначены для студентов экономических специальностей.

Утверждены и рекомендованы к изданию кафедрой экономического анализа и статистики (протокол №2 от 14.02.2008 г.).

 Шелковников С.А., 2010

 Экономический институт, 2010

Показатели измерения общего риска

Риск – категория вероятностная, поэтому методы его количественной оценки базируются на ряде важнейших по­нятий теории вероятностей и математической статистики. «Ситуация риска» связана со стохастическими процес­сами, которым сопутствуют три сосуществующих условия:

• наличие неопределенности;

• необходимость выбора альтернатив (отказ от выбора – это разновидность выбора);

• оценка вероятности осуществления выбираемых аль­тернатив.

Результат явления с неопределенным (заранее неизвест­ным) исходом определяется неким случайным событием, экспериментом, выбором.

Случайным называется событие, которое при данном на­боре условий может либо произойти, либо не произойти. Ко­личественное измерение степени достоверности реализации случайных событий основывается на понятии вероятности.

Вероятностная оценка – наиболее очевидный способ оценки риска.

Вероятность означает возможность получения опреде­ленного результата. Методы теории вероятности сводятся к определению вероятности наступления определенных со­бытий и выбору из нескольких возможных событий самого вероятного, которому соответствует наибольшее численное значение математического ожидания.

Под вероятностью р события Е понимается отноше­ние числа К случаев, благоприятствующих наступлению этого события, к общему числу N всех равновозможных случаев.

К важнейшим свойствам вероятности относятся следу­ющие.

Вероятность события есть число неотрицательное:

р(Е)≥0.

Вероятность достоверного события, т.е. события, которое при данном комплексе условий непременно произой­дет, равна 1; вероятность невозможного события равна 0.

Вероятность события может принимать значения, лежащие в диапазоне от 0 до 1:

0≤Р(Е)≤1.

Вероятность наступления события может быть опреде­лена объективным или субъективным методом.

Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие. Например, вероятность выпадения «орла» или «решки» при подбрасывании идеальной монеты – 0,5.

Субъективный метод основан на использовании субъек­тивных критериев (суждение оценивающего, его личный опыт, оценка эксперта), и вероятность события в этом слу­чае может быть разной, будучи оцененной разными экспер­тами.

Задача. Контрольная партия – 98 шт. Брак – 7 шт. Какова вероятность того, что наугад взятая деталь – бракованная.

Ответ: р =________________=

Из 100 отобранных образцов 10 содержали дефект А и 20 – дефект Б. Определить вероятность того, что случайно отобранный образец будет иметь только один дефект А или Б.

Ответ: р(А+Б) = р(А) + р(Б) – р(АБ) = _______________________________________

Вероятность поломки детали А у комбайна в течение уборки р(А) = 0,025, вероятность поломки детали Б р(Б) = 0,04. Найти вероятность поломки обеих деталей в течение уборки.

Ответ: р(АБ) = р(А) х р(Б) =______________________ =

Случайные величины и законы их распределения

Случайной называется величина, которая в результате опыта может принимать различные или заранее неизвест­ные значения. Случайные величины делят на дискретные и непрерывные. В процессе количественного анализа фи­нансовых рисков обычно используются дискретные случай­ные величины.

Величина Е называется дискретной случайной вели­чиной, если множество ее возможных значений х₁, х₂, ..., х_n конечно или счетно и принятие ею каждого из указанных значений есть случайное событие с определенной вероят­ностью.

В нашем примере случайная величина доходности по ак­циям является дискретной, поскольку мы можем перечис­лить или перенумеровать все ее значения.

Любое правило, позволяющее находить вероятности всех значений случайной величины, называют законом распре­деления ее вероятностей.

Для дискретной случайной величины этот закон задает­ся в виде таблицы, в которой перечисляют все ее возмож­ные значения и их вероятности. При этом если число ее значений конечно, сумма их вероятностей равна 1.

Пример закон распре­деления вероятности приведен в таблице.

Прогнозируемая доходность по акциям фирмы

Событие	Доходность, %	Вероятность
Высокий спрос	12	1/3
Средний спрос	9	1/3
Низкий спрос	6	1/3

В общем случае количество возможных сценариев может быть очень большим, что затрудняет табличное представле­ние закона распределения. Поэтому для удобства проведе­ния анализа распределения дискретные случайные величины аппроксимируют непрерывными распределениями, позволя­ющими использовать сравнительно простые методы расче­тов даже при неограниченном количестве сценариев. Для за­дания таких распределений используется функция F(х), назы­ваемая функцией распределения случайной величины.

Функция F(x) или ее производная (плотность распреде­ления) дают полную информацию о законе распределения случайной величины.

Большинство результатов хозяйственной деятельности, рассматриваемые как случайные величины, подчиняются закону, близкому к нормальному. График нормального распределения описывается так называемой нормальной кривой, или кривой Гаусса (рис.).

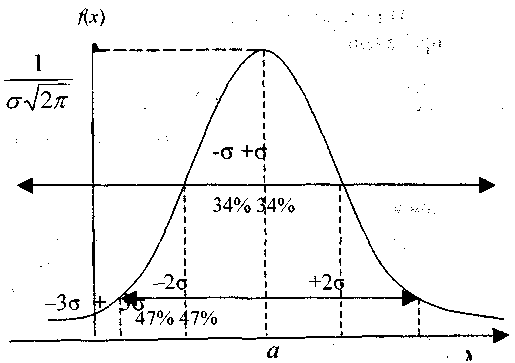
Отметим некоторые важные свойства графика функции нормального распределения.

Площадь, ограниченная нормальной кривой, равна единице;

Средняя арифметическая величина - а, определяет центр распределения, и ее размерность совпадает с размерностью случайной величины. Среднеквадратическое отклонение σ определяет разброс значений случайных величин относительно центра распределения.

Чем больше а, тем правее расположен график (при одинаковых σ); чем больше σ, тем более пологий график (при одинаковых а). Чем больше среднеквадратическое отклонение исследуемой характеристики, тем больший риск она содержит, тем более неопределенно ее значение в будущем. Если случайная величина распределена нормально, то вероятность попадания случайной величины х в заданный интервал (α; β) определяется функцией Лапласа:

где

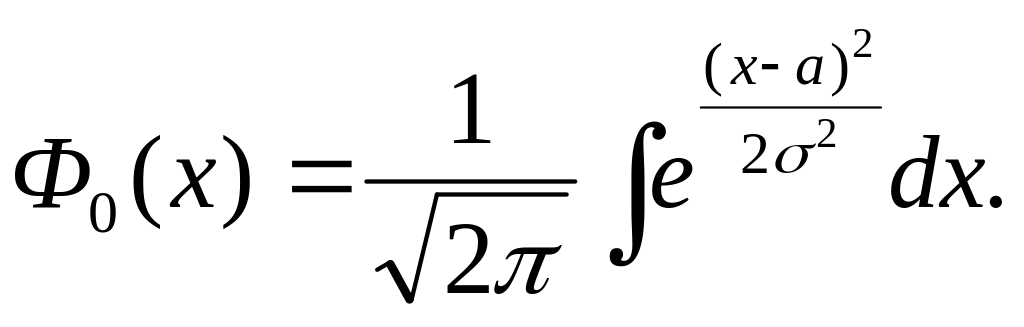
Задача. На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием 950 кг и средним квадратическим отклонением 150 кг.

Определите вероятность того, что вес случайно отобранной туши:

а) окажется больше 1100 кг;

Ответ: р(Х > 1100) = ____________________________

б) окажется меньше 650 кг;

Ответ: р(Х < 650) = _____________________________

в) будет находиться между 800 и 1100 кг;

Ответ: р(800 < Х < 1100) = ______________________________________________________

г) отклонится от математического ожидания меньше, чем на 300 кг.

Используем формулу расчета вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания

где a – величина отклонения случайной величины Х от математического ожидания.

По условию Δ = ____; а = ____, σ = ______. Используя эту формулу, получим

Р(|Х - 950| < 150) = _____________________________________________.

д) отклонится от математического ожидания больше, чем на 150 кг, т.е.

Р(|Х - 950|) >150) = ?

Это вероятность события, противоположного по отношению к событию, – вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 150 кг,

Р(|Х - 950| < 150). Следовательно,

Р(|Х - 950|) > 150) = 1 - Р(|Х - 950| < 150) = _________________________________.

Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 150 кг, составляет ____________.

Можно использовать другой алгоритм решения.

Р(|Х - 950| > 150) = Р(Х < 800) + Р(Х > 1100) = __________________________________.