5. Невозможный мир Эшера.

Роджер Пенроуз начал заниматься невозможными объектами под влияние лекции Эшера, но его математические работы в свою очередь оказали свое влияние на творчество художника. В 1961 году М. К. Эшер под впечатлением невозможного треугольника, нарисованного Пенроузом (Пенроузы отослали копию статьи Эшеру) создал знаменитые литографии "Водопад" и "Возхождение и спуск"

Рассмотрим знаменитую картину Мориса Эшера "Водопад" и ее упрощенную компьютерную модель, выполненную в фотореалистичном стиле (см. рис. 7). На первый взгляд перед нами обыкновенная картина, изображающая... чертеж вечного двигателя!!! Но ведь, как известно из школьного курса физики, вечный двигатель невозможен! Как же Эшеру удалось с такими подробностями изобразить то, чего в природе вообще не может быть?!

Рисунок 7. Вечный двигатель на гравюре "Водопад" Эшера.

Рисунок 8. Компьютерная модель вечного двигателя Эшера

При попытке соорудить двигатель согласно чертежу (или при внимательном анализе последнего), "обман" всплывает сразу - в трехмерном пространстве такие конструкции геометрически противоречивы и могут существовать только на бумаге, то есть на плоскости, а иллюзия "объема" создается лишь за счет признаков перспективы (в данном случае - умышленно искаженных).

Другая известная работа Пенроуза (повторенная в гравюре Эшера "Бесконечный спуск") изображена на рис. 9. Как видно, она представляет собой разновидность "Водопада", трансформированную в лестницу, ведущую в вечность, по которой можно подниматься (спускаться) бесконечно. Если бросить на лестницу мячик, то мы получим вполне конкретный вечный двигатель.

  Рисунок 9. Лестница Пенроуза и "Бесконечный спуск"/"Ascendiendo descendiendo

А вот пара невозможных фигур, созданных Оскаром Реутерсвардом (см. рис. 12). Это хоть и не вечные двигатели, но идея, лежащая в их основе, все та же - изображение объемного пространства на плоскости, которое не соответствует никакой физической действительности.

 

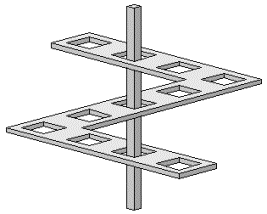
Рисунок 12. Пара невозможных фигур от Оскара Реутерсварда

6. "Чертова вилка".

Существует группа невозможных объектов, скульптурная реализация которых невозможна. Самая, пожалуй, известная из них - "невозможный трезубец", или "чертова вилка" (Р3-1). Если внимательно присмотреться к объекту, можно заметить, что три зубца постепенно переходят в два на общем основании, приводя к конфликту восприятия. Мы сравниваем число зубцов сверху и снизу и приходим к выводу о невозможности объекта

.

Рисунок 14.

На основе "вилки" создано великое множество невозможных объектов, в том числе таких, где цилиндрическая на одном конце деталь становится квадратной на другом.

Невозможные фигуры - возможны!

Знакомство с невозможными фигурами (особенно в исполнении Эшера), конечно, ошеломляет, но тот факт, что любую из невозможных фигур возможно сконструировать в реальном трехмерном мире удивляет гораздо больше. Как известно, всякое двухмерное изображение представляет собой проекцию трехмерной фигуры на плоскость (лист бумаги). Способов проекции существует достаточно много, но в рамках каждого из них (например, аксонометрической проекции) отображение выполняется однозначно, то есть существует строгое соответствие между трехмерной фигурой и ее двухмерным изображением. Однако аксонометрические, изометрические и другие популярные способы проекции являются однонаправленными преобразованиями, осуществляемыми с потерей информации и потому обратное преобразование может быть выполнено бесконечным множеством способов, то есть двухмерному изображению соответствует бесконечное множество трехмерных фигур и любой математик без труда докажет, что такое преобразование возможно для любого двухмерного изображения. То есть, на самом деле никаких невозможных фигур нет!

Вернемся к треугольнику Пенроуза и попробуем соорудить трехмерную фигуру, проекция которой на двухмерную плоскость выглядела бы обозначенным образом. Естественно, "в лоб" такую задачу решить не удастся, но если хорошо покурить и выбрать правильный ракурс, то... один из возможных вариантов показан на рис. 16.

Рисунок 16. Возможный невозможный Треугольник Пенроуза.

Многие считают, что невозможные фигуры действительно невозможны, и они не могут быть созданы в реальном мире. Однако из школьного курса геометрии нам известно, что чертеж, изображенный на листе бумаги, является проекцией трехмерной фигуры на плоскость. Следовательно, любая фигура, нарисованная на листе бумаги должна существовать в трехмерном пространстве. Причем трехмерных объектов, при проецировании на плоскость которых, получается заданная плоская фигура бесконечное множество. Это же относится и к невозможным фигурам. Конечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Например, если вы возьмете три одинаковых деревянных бруска, вы не сможете совместить их так, чтобы получился невозможный треугольник. Однако, при проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга, стыковаться друг с другом и т.п.

С древних времен люди пытались изображать животных, предметы быта, пейзажи на скале, глиняной дощечке, бересте, а позднее на бумаге и холсте. Чтобы изображать на листе бумаги объемный предмет мы не задумываемся над тем, как же можно его, имеющего три измерения / длину, ширину и высоту / втиснуть в бумагу, которая имеет всего два измерения, Мы идем на условности. Законы линейной и воздушной перспективы помогают нам отобразить глубину. Получается, что мы стараемся втиснуть объем в плоскость, приучая наше сознание к этому. Нас до определенной степени устраивают фотографии, кино и телеизображение, которые в сущности тоже самое. Таким образом, зная как человек воспринимает двухмерное изображение, можно создавать на плоскости невозможные фигуры. На первый взгляд, это обыкновенная фигура, но при более пристальном рассмотрении, а точнее после того, как вы начинаете ее представлять в трехмерном пространстве, сразу же ощутите, что она необычна и что - то не вписывается в ваше привычное представление. Вот так же случайно Ройтерсверд нарисовал свой треугольник и понял, что сделать такого рода фигуры в пространстве невозможно. Их можно лишь изображать на плоскости, придавая им объем за счет правильного распределения теней. Для людей, склонных к изобретательству, невозможные фигуры являются своеобразным рычагом для создания чего - то нового, необычного. Они способны направить творческие возможности человека в новое русло, изменить пространственное мышление, воображение.

Кстати говоря, Треугольник Пенроуза увековечен в виде статуи в Перте (Австралия). Созданный усилиями художника Брайна МакКея и архитектора Ахмада Абаса, он был воздвигнут в парке Клайзебрук в 1999 году и теперь все проезжающие мимо могут видеть следующую "невозможную" фигуру (см. рис. 17). Стоит изменить угол зрения, как треугольник из "невозможного" превращается в реальное и эстетически непривлекательное сооружение, не имеющее к треугольникам никакого отношения.

Рисунок 17

Заключение.

Невозможные фигуры находят иногда неожиданное применение. Оскар Рутесвард рассказывает в книге "Omojliga figurer" об использовании рисунков имп-арта для психотерапии. Он пишет, что картины своими парадоксами вызывают удивление, заостряют внимание и желание расшифровать. В Швеции их применяют в зубоврачебной практике: рассматривая картины в приемной, пациенты отвлекаются от неприятных мыслей перед кабинетом стоматолога.

Невозможные объекты заставляют наш разум сначала увидеть то, чего по нашим привычным меркам быть не должно, затем искать ответ - что же сделано не так, в чем скрыта изюминка парадокса. А ответ найти порой не так - то просто - он скрыт в оптическом, психологическом, логическом восприятии рисунков. Для людей, склонных к изобретательству, невозможные фигуры являются своеобразным рычагом для создания чего-то нового, необычного.

Математики утверждают, что и дворцы, в которых можно спуститься вниз по лестнице, ведущей вверх, могут существовать. Для этого нужно лишь построить такое сооружение не в трехмерном, а, скажем, в четырехмерном пространстве. А уж в виртуальном мире, который открывает нам современная компьютерная техника, и не такое можно натворить. Вот так в наши дни осуществляются задумки человека, который еще на заре века поверил в существование невозможных миров.

Развитие технических исследований, необходимость мыслить по-новому, поиски прекрасного - все эти требования современной жизни заставляют искать новые способы, которые способны направить творческие возможности человека в новое русло, изменить пространственное мышление, воображение.

В процессе выполнения своей работы я актуализировал тему «Невозможные фигуры». Представляя свою работу на различных форумах, получил ответный всплеск интереса к теме. Многие услышали об этой теме впервые и теперь, благодаря моей работе, смогут расширить свой кругозор. Мое исследование по развитию наглядных представлений привлекло внимание учителей математики нашего лицея, а собранный мною иллюстративный материал, был использован в работе с младшими школьниками. Я считаю, что поставленная мною цель была достигнута.

Список литературы и источников.

1. Левитин Карл Геометрическая рапсодия. - М.: Знание, 1984, -176 с.

2. Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26

3. Реутерсвард О. Невозможные фигуры. – М.: Стройиздат,1990, 206 с.

4. Ткачева М.В. Вращающиеся кубики. – М.: Дрофа, 2002. – 168 с.

5. http://wikipedia.tomsk.ru

6. http://www.konenko.net/imp.htm

7. http://www.im-possible.info/russian/articles/reut_imp/

Приложение.

Исследование усвоения геометрического материала и развития пространственных представлений у учащихся школы.

Кенгуру - выпускникам.
9 класс
разделы программы	2008	2009	2010
целые числа	66	80	64
числовые выражения	76	88,6	67
геометрические фигуры	25	67	67
вычисления в геометрии	33	38	54
общие умения и навыки		2009	2010
определения фактов		69	64,3
стандартные алгоритмы		67	62,1
наглядные представления		59	37,6
11 класс
разделы программы	2006	2007	2008	2009	2010
числа	91	63	64		78
тождества	90	42	38	59	66
геометрические фигуры	69	31	34	30	52
вычисления в геометрии	46	32	19	23	36
общие умения и навыки				2009	2010
определения фактов				52,3	64
стандартные алгоритмы				58	54
наглядные представления				23,5	31