
- •Основные принципы системного подхода к моделированию экономических систем
- •Производственные функции.
- •Основные типы макроэкономических производственных функций (аналог 2)
- •Модель Леонтьева
- •Модель Солоу
- •Золотое правило накопления
- •Оптимизация нормы накопления
- •Свойства функции полезности
- •Загальна модель споживчого вибору. Модель Стоуна
- •Взаимозаменяемость благ и эффекты компенсации. Уравнение Слуцкого
Основные принципы системного подхода к моделированию экономических систем
Система – сущность, которая в результате взаимодействия ее частей может поддерживать свое существование и функционировать как единое целое
Система обладает эмерджентными свойствами (возникающими) – свойствами, которых нет ни у одной их их частей. Разобрав систему на части, проанализировав каждую из низ нельзя сделать вывод о свойствах целой системы
Системный подход — направление методологии исследования, в основе которого лежит рассмотрение объекта как целостного множества элементов в совокупности отношений и связей между ними, то есть рассмотрение объекта как системы.
Говоря о системном подходе, можно говорить о некотором способе организации наших действий, таком, который охватывает любой род деятельности, выявляя закономерности и взаимосвязи с целью их более эффективного использования. При этом системный подход является не столько методом решения задач, сколько методом постановки задач.
Проблема системности - непонимание одним специалистом другого.
Основные принципы системного подхода
Целостность, позволяющая рассматривать одновременно систему как единое целое и в то же время как подсистему для вышестоящих уровней.
Иерархичность строения, то есть наличие множества (по крайней мере, двух) элементов, расположенных на основе подчинения элементов низшего уровня элементам высшего уровня. Реализация этого принципа хорошо видна на примере любой конкретной организации. Как известно, любая организация представляет собой взаимодействие двух подсистем: управляющей и управляемой. Одна подчиняется другой.
Структуризация, позволяющая анализировать элементы системы и их взаимосвязи в рамках конкретной организационной структуры. Как правило, процесс функционирования системы обусловлен не столько свойствами её отдельных элементов, сколько свойствами самой структуры.
Множественность, позволяющая использовать множество кибернетических, экономических и математических моделей для описания отдельных элементов и системы в целом.
Производственные функции.
Производственная функция (функция производства) — экономико-математическая количественная зависимость между величинами выпуска (количество продукции) и факторами производства, (затраты ресурсов, уровень технологий и др.) может выражаться как множество изоквант
Агрегированная производственная функция может описывать объёмы выпуска народного хозяйства в целом.
В зависимости от анализа влияния факторов производства на объём выпуска в определённый момент времени или в разные промежутки времени производственные функции делятся на статические: P = f(x1,x2,...,xn) и динамические: P = f(x1(t),...,xk(t),...,xn).
Линейные.P= a1*x1+…+an*xn
Мультипликативно-степенные. Это функции вида P=П i=1 до n (xi^alfai)
Такие производственные функции при отсутствии одного из факторов обращаются в ноль.
Функция Кобба-Дугласа: P = A * L^lamda*K^(1-Lamda)
Модель Солоу
![]()
![]()
![]() -
склонность к сбережению
-
склонность к сбережению
![]()
![]() – фондовооружённость;
– фондовооружённость;
![]() – удельное потребление;
– удельное потребление;
![]() – доля потребления (какая часть продукта
идёт на потребление);
– доля потребления (какая часть продукта
идёт на потребление);
![]() – доля накопления;
– доля накопления;
![]() – производительность
– производительность
![]()
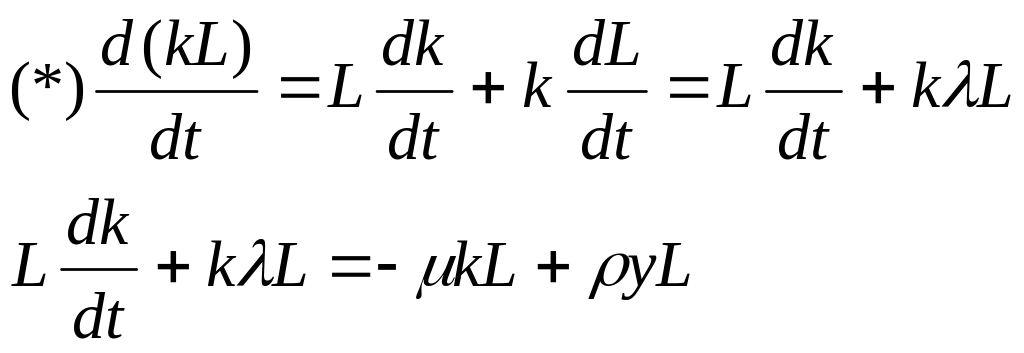
Функция CES:
Особая проблема — учет в макроэкономических ПФ фактора технического прогресса. С помощью ПФ изучается также эквивалентная взаимозаменяемость факторов производства, которая может быть либо неизменной, либо переменной (т. е. зависимой от объемов ресурсов). Соответственно функции делят на два вида: с постоянной эластичностью (CES) замены и с переменной (VES)
Функция CES, как и функция Кобба— Дугласа, исходит из допущения о постоянном убывании предельной нормы замещения используемых ресурсов. Между тем эластичность замещения капитала трудом и, наоборот, труда капиталом в функции Кобба—Дугласа, равная единице, здесь может принимать различные значения, не равные единице, хотя и является постоянной. Наконец, в отличие от функции Кобба—Дугласа логарифмирование функции CES не приводит ее к линейному виду, что вынуждает использовать для оценки параметров более сложные методы нелинейного регрессионного анализа.
P= A ((1-alfa)*K^-b + alfa*L^-b)^ (-c/b)
в этом случае эластичность замещения ресурсов не зависит ни от K, ни от L и, следовательно, постоянна: Ekl= 1/(1+b)
