
- •Основные принципы системного подхода к моделированию экономических систем
- •Производственные функции.
- •Основные типы макроэкономических производственных функций (аналог 2)
- •Модель Леонтьева
- •Модель Солоу
- •Золотое правило накопления
- •Оптимизация нормы накопления
- •Свойства функции полезности
- •Загальна модель споживчого вибору. Модель Стоуна
- •Взаимозаменяемость благ и эффекты компенсации. Уравнение Слуцкого
Свойства функции полезности
Функция полезности дважды дифференцируема и имеет непрерывные вторые частные производные.

Частная производная (3.2.1) называется предельной полезностью товара вида i.
Т.о. для любого набора товаров возрастание потребления товара вида i при постоянном уровне потребления других товаров приводит к увеличению полезности.
Выполнены условия:

Это
неравенство говорит о том, что предельная
полезность
![]() товара
уменьшается по мере того, как продукт
потребляется.
товара
уменьшается по мере того, как продукт
потребляется.
Загальна модель споживчого вибору. Модель Стоуна
Модель задачи потребительского выбора имеет вид:
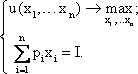
Множество всевозможных товаров, доступных потребителю при ценах p и доходе K:
![]()
называетсяе бюджетным множеством.
Граница
![]()
множества
![]() называется
бюджетной линией.
называется
бюджетной линией.
Оптимальным
решением задачи называется такой вектор
![]() ,
что
,
что
![]()
В новой формулировке задача потребительского выбора представляет собой задачу нелинейного программирования.
Для решения данной задачи составим функцию Лагранжа:
![]()
и найдем ее точки максимума. Точки, в которых функция Лагранжа достигает своего максимума, находятся среди стационарных точек, удовлетворяющих условиям:
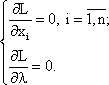
Отсюда мы получаем условия первого порядка решения задачи потребительского выбора:
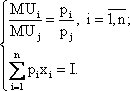
Решение задачи потребительского выбора записывается в виде функций спроса Маршалла:
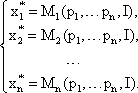
Модель Стоуна
Выведем функцию спроса для конкретной функции потребительского предпочтения, называемой функцией Стоуна и имеющей следующий вид:
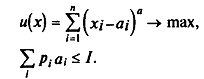 некоторые авторы дают не аддитивную, а
мультипликативную ее форму (произв
вместо суммы)
некоторые авторы дают не аддитивную, а
мультипликативную ее форму (произв
вместо суммы)
Здесь а, — минимальное необходимое
количество i-го блага,
которое приобретается в любом случае
и не является предметом выбора. Для того
чтобы набор {ai} мог быть
полностью приобретен, необходимо, чтобы
доход I был больше общего
количества денег, необходимого для
покупки этого набора, т. е.
![]()
Взаимозаменяемость благ и эффекты компенсации. Уравнение Слуцкого
Если функция спроса имеет вид хi=I/npi
(при сi неравных между
собой,
![]() ),
, то спрос на i-й товар не
зависит от цены на любой j-й
товар. Если при росте цены на товар i,
при снижении спроса на i-й
товар растет спрос на товар j,
то эти товары взаимозаменяемы. Наоборот,
если спрос на j-й товар
также падает, они взаимодополняемы.
Реальная взаимозаменяемость может
искажаться общим снижением благосостояния
при росте цены i-го блага:j-е
благо можетзаменять i-е
в потреблении, но спрос на него может
не расти, так как снизилось общее
благосостояние потребителя. Для
исключения этого искажения используют
понятие компенсированного изменения
цены (такого, которое сопровождается
увеличением дохода потребителя для
поддержания прежнего уровня благосостояния).
),
, то спрос на i-й товар не
зависит от цены на любой j-й
товар. Если при росте цены на товар i,
при снижении спроса на i-й
товар растет спрос на товар j,
то эти товары взаимозаменяемы. Наоборот,
если спрос на j-й товар
также падает, они взаимодополняемы.
Реальная взаимозаменяемость может
искажаться общим снижением благосостояния
при росте цены i-го блага:j-е
благо можетзаменять i-е
в потреблении, но спрос на него может
не расти, так как снизилось общее
благосостояние потребителя. Для
исключения этого искажения используют
понятие компенсированного изменения
цены (такого, которое сопровождается
увеличением дохода потребителя для
поддержания прежнего уровня благосостояния).
Уравнение Слуцкого — уравнение, смысл которого состоит в том, что изменение спроса на некоторый товар при повышении или снижении его цены складывается из влияния непосредственного изменения спроса и косвенного влияния в результате переключения спроса на другие товары.
Изменение спроса = эффект изменения дохода + эффект замещения
![]()
Блага i и j называются
взаимозаменяемыми, если
![]() ,
и взаимодополняемыми, если
,
и взаимодополняемыми, если
![]()
