Задача 86[10]
Укажите разложение на линейные множители для многочленов
а)
;
б)
;
в)
;
г)
.
Решение а)
;
б)
;
в)
;
г)
;
Схема доказательства основной теоремы алгебры
Непрерывность — отображение кривых
Пусть есть некоторый многочлен:
Тогда если мы будем медленно менять , то число тоже будет меняться медленно. Если будет двигаться по непрерывной прямой в комплексной плоскости, то тоже будет двигаться по некоторой непрерывной кривой.
Например, пусть движется по окружности
Тогда
будет
тоже двигать по некоторой кривой в
комплексной плоскости — малое
изменение
будет
вызывать малое смещение
.
Таким образом, мы можем говорить об
отображении кривых — под действием
многочлена
одна
кривая превращается в другую кривую.
На рисунке 12 изображена кривая, в которую
отобразится окружность
при
отображении
,
.
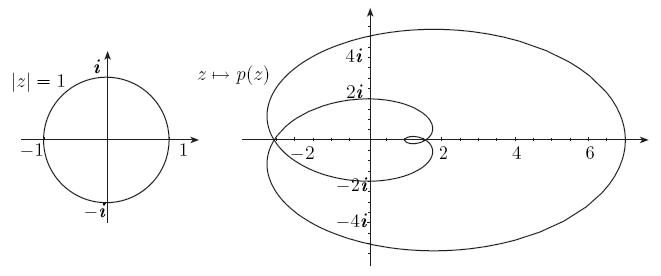
Рис. 12 Образ окружности
под
действием отображения
,
Доминирование старшей степени
Как будет двигаться
если
и
движется
по окружности
?
Другими словами, как выглядит образ
окружности
при
отображении
?
Заметьте, что
,
поэтому образ этой окружности будет
снова окружность, только в то время, как
сделает
один оборот по окружности
сделает
оборотов:
Если
сделает
оборот по окружности радиуса
),
то
сделает
оборотов
по окружности радиуса
).
Свойство доминирования старшей
степени заключается в том, что при
очень больших по модулю значениях
в
значение многочлена
больший
вклад вносит старший член
.
Например, если
,
то после подстановки в
получим:
После того, как мы вынесли за скобку
,
в скобках осталось только одно слагаемое,
которое не содержит
.
Все слагаемые кроме первого, при
уменьшаются
и становятся совсем маленькими и не
значительными. На рисунке 13 изображены
образы трех окружностей радиусов
,
,
—
чем больше радиус, тем больше его образ
похож на три оборота вокруг центра.
Непрерывность — движение кривых
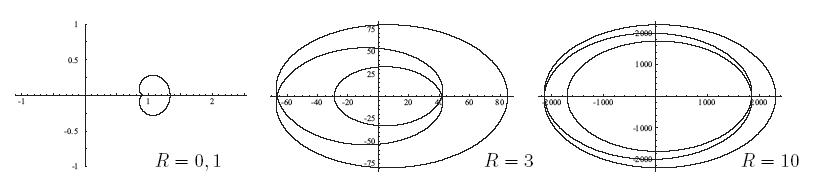
Рис. 13 Образ окружностей
,
и
под
действием отображения
,
.
А теперь представьте, что мы начали
непрерывно менять
(например,
от
до
).
Тогда образ окружности
при
отображении
,
,
постепенно будет деформироваться.
Сначала, при
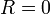это
будет просто точка
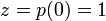.Потом, при маленьком , например
,
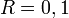вокруг точки
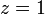появится
некоторая замкнутая кривая (рис. 13).Потом, при некоторых средних значениях , например
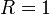,будем
иметь нечто необычное (рис. 12 справа).Потом, постепенно увеличивая до
,
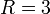получим три ярко выраженных оборота
(рис. 13}).При больших , например
,
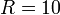обороты все больше будут сближаться
друг к другу и выглядеть почти как
окружностей.
(рис. 13).
Во время этой деформации кривая в
какой-то момент пройдёт через точку
.
Действительно, при маленьком
точка
находится
снаружи замкнутой кривой, а при больших
—
внутри замкнутой кривой, которая, более
того, делает вокруг
несколько
оборотов. Это означает, что при некотором
и
некотором
получим
,
и, следовательно,
является
корнем нашего многочлена. Таким образом,
наш многочлен
точно
имеет хотя бы один комплексный корень.
Конец схемы доказательства