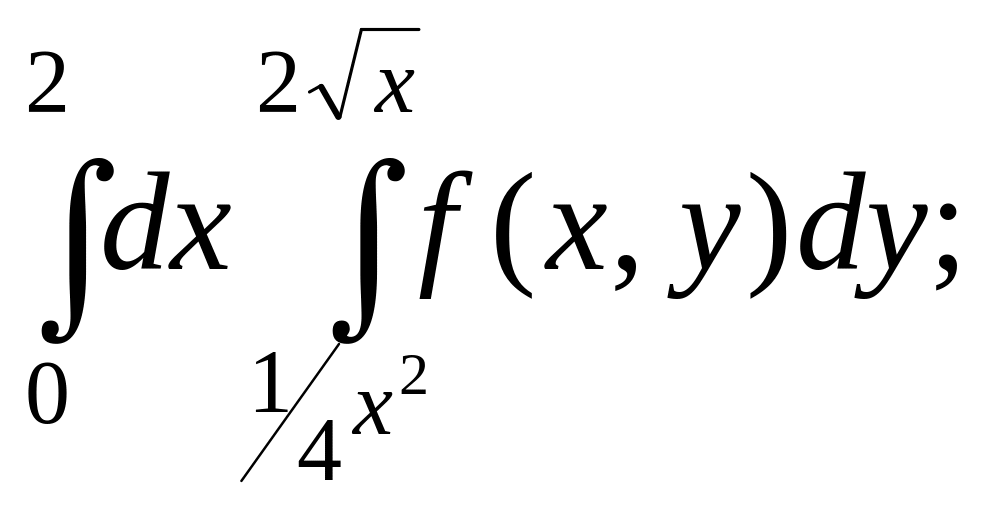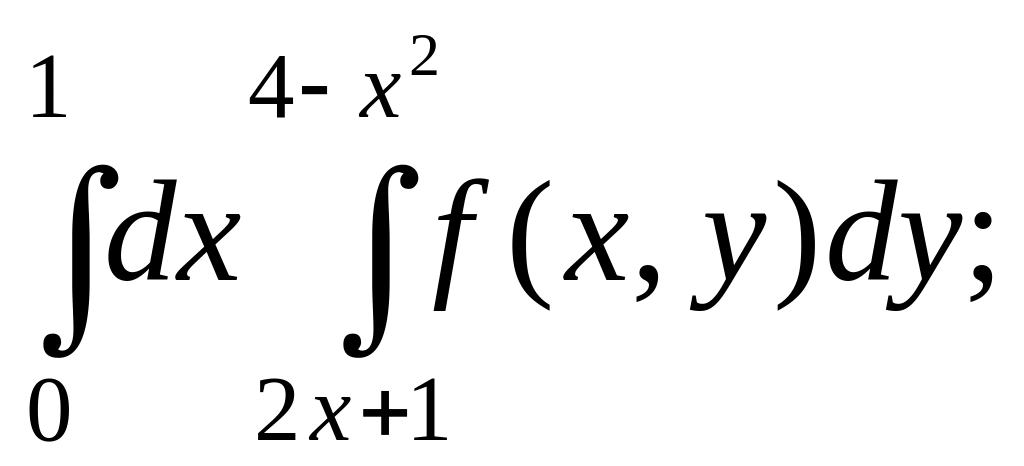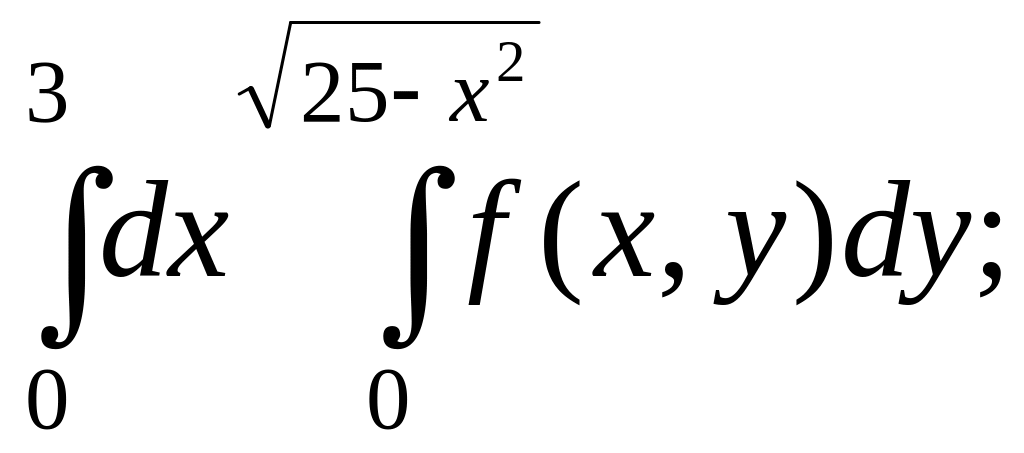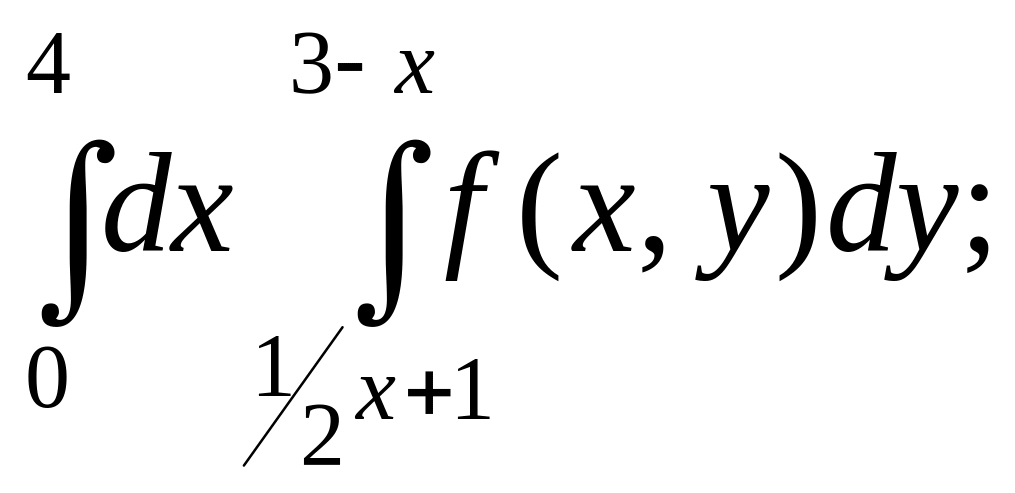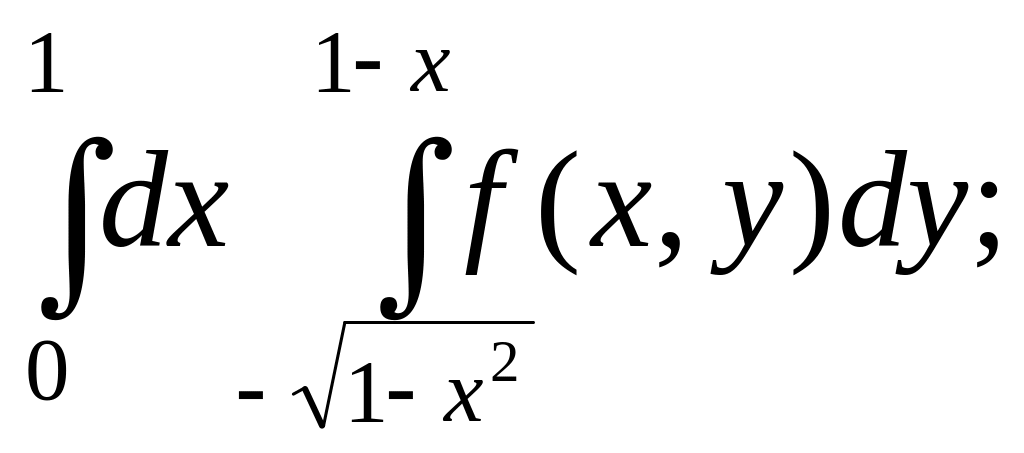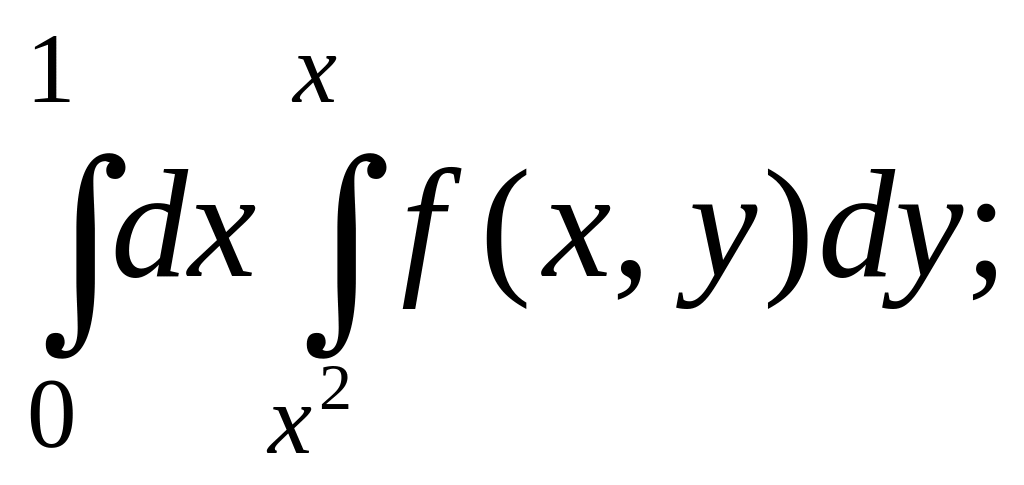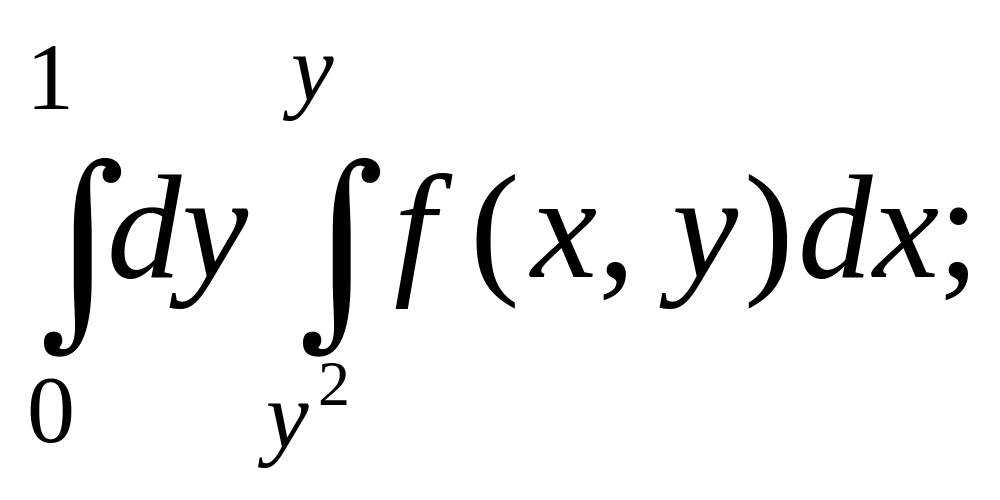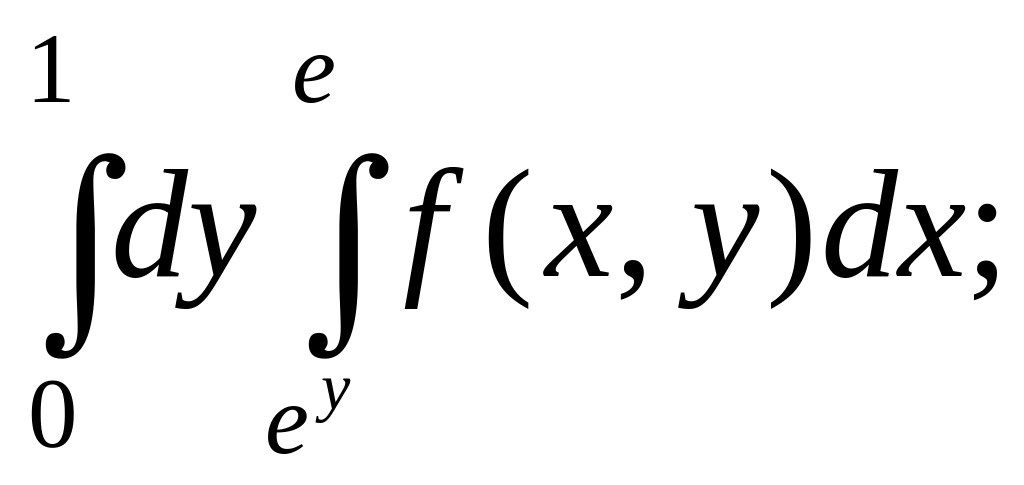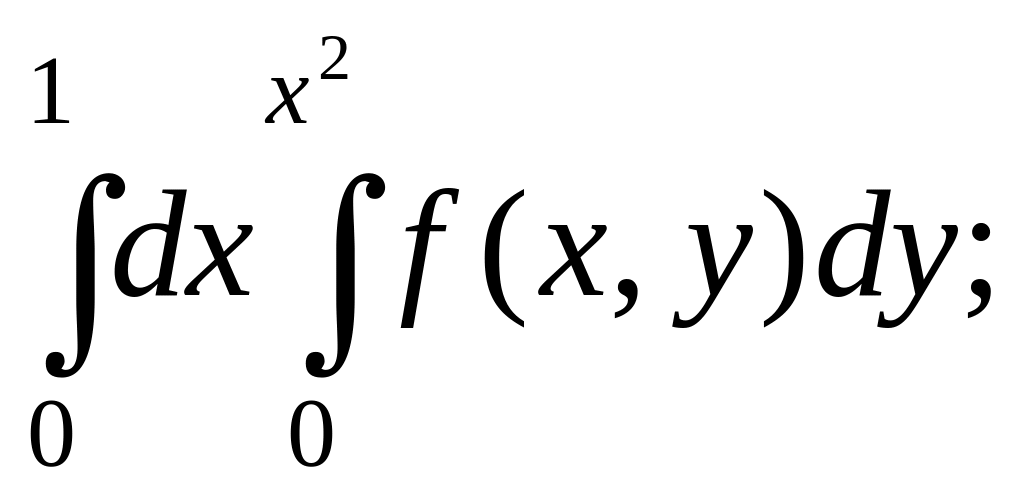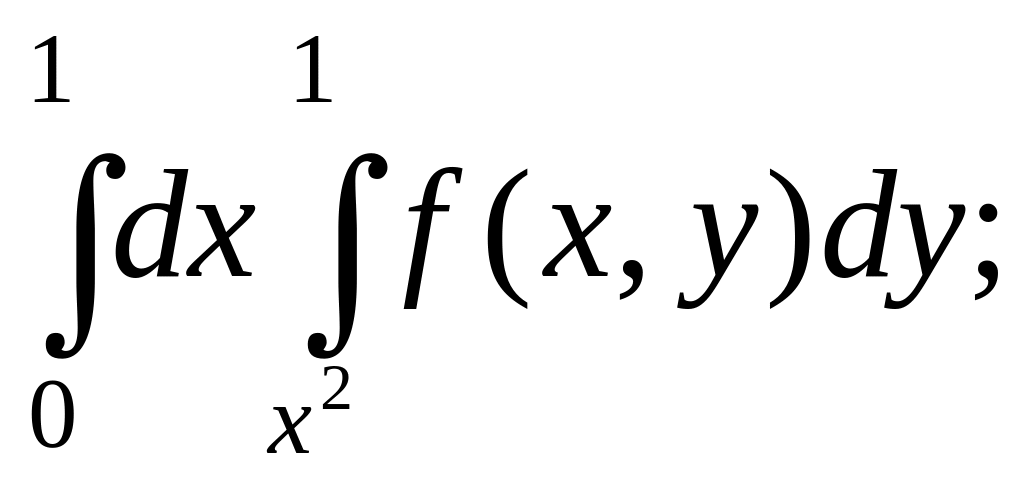- •Міністерство освіти і науки україни
- •Частина і. Подвійні інтеграли
- •Визначення, теорема існування та властивості подвійного інтеграла
- •Основні властивості подвійних інтегралів
- •1.2. Обчислення подвійних інтегралів в декартових координатах. Застосування зміни порядку інтегрування
- •Обчислення подвійних інтегралів в полярних координатах
- •Застосування подвійних інтегралів для обчислення площ плоских фігур, об’ємів циліндроїдів та площ поверхонь
- •Застосування подвійних інтегралів для обчислення маси, статичних моментів і моментів інерції та координат центра ваги плоских фігур
- •Частина іі. Потрійні інтеграли
- •2.1. Означення, теорема існування та властивості
- •Обчислення потрійних інтегралів в декартових, циліндричних та сферичних координатах
- •Розв’язання.
- •Застосування потрійних інтегралів для обчислення об’ємів
- •] Частина ііі. Завдання для самостійної роботи
- •3.1. Варіанти завдань а), б), в)
- •Для самостійної роботи з подвійних інтегралів
- •3.2. Варіанти завдань г), д), е) для самостійної роботи з потрійних інтегралів
Розв’язання.
а) Обчислення потрійного інтегралу в декартових координатах.
Очевидно,
що в даному випадку
![]() ,
,
![]() ,
,
![]() .
Тому за формулою (2.4) маємо:
.
Тому за формулою (2.4) маємо:
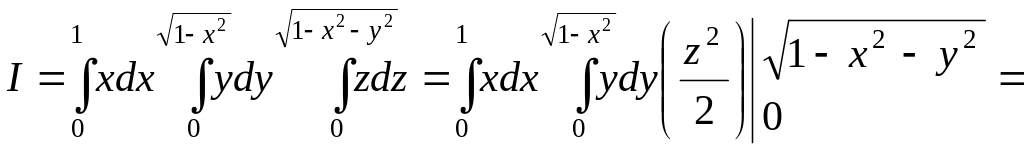
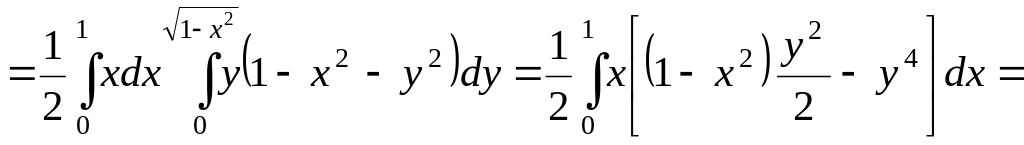
![]() ;
;
б) Обчислення потрійного інтеграла в циліндричних координатах ( , , ).
Очевидно,
що в даному випадку
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тому за формулою (2.5) маємо:
.
Тому за формулою (2.5) маємо:
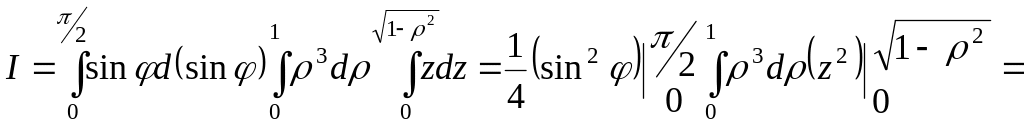
![]() ;
;
в) Обчислення потрійного інтеграла в сферичних координатах ( , , ).
Очевидно,
що в даному випадку
,
![]() ,
,
![]() ,
(
,
(![]() ).
Тоді за формулою (2.6) маємо:
).
Тоді за формулою (2.6) маємо:
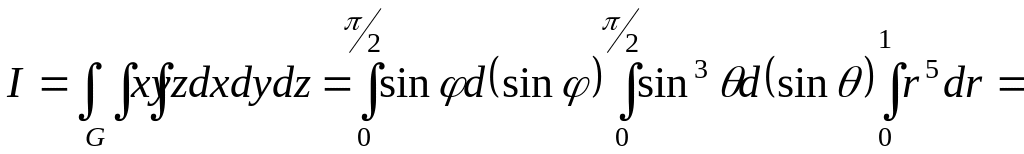
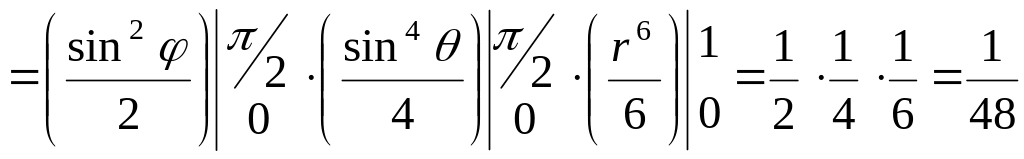 .
.
Застосування потрійних інтегралів для обчислення об’ємів
просторових тіл в декартових, циліндричних
та сферичних координатах
Об’єм просторового тіла, що займає область , визначається за формулами:
![]() (в декартових
координатах) (2.7)
(в декартових
координатах) (2.7)
![]() (в циліндричних
координатах) (2.8)
(в циліндричних
координатах) (2.8)
![]() (в сферичних
координатах) (2.9)
(в сферичних
координатах) (2.9)
Процедура
обчислення об’єму просторового тіла
принципово не відрізняється від
обчислення потрійного інтеграла, в
якому
![]() .
.
Застосування потрійних інтегралів для обчислення маси,
статичних моментів, моментів інерції
та координат центра ваги
Зазначені застосування належать до механічних застосувань потрійних інтегралів.
Якщо
– деяка область простору, яку займає
матеріальне тіло з густиною
![]() ,
то:
,
то:
а) Маса тіла
,
що має об’єм
![]() ,
визначається формулою:
,
визначається формулою:
![]() ,
(2.10)
,
(2.10)
б) Статичні
моменти
![]() ,
,
![]() ,
,
![]() тіла
відносно координатних площин
,
,
визначаються формулами:
тіла
відносно координатних площин
,
,
визначаються формулами:
![]() ,
,
![]() ,
(2.11)
,
(2.11)
![]() .
.
в) Координати центра ваги визначаються формулами:
![]() ,
,
![]() ,
,
![]() .
(2.12)
.
(2.12)
г) Моменти
інерції
![]() ,
,
![]() ,
,
![]() відносно координатних осей
,
,
,
момент інерції
відносно координатних осей
,
,
,
момент інерції
![]() ,
,
![]() ,
,
![]() відносно координатних площин
,
,
і момент інерції
відносно початку координат визначаються
формулами відповідно:
відносно координатних площин
,
,
і момент інерції
відносно початку координат визначаються
формулами відповідно:
![]() ,
,
![]() ,
(2.13)
,
(2.13)
![]()
![]() ,
,
![]() ,
(2.14)
,
(2.14)
![]()
![]() (2.15)
(2.15)
Приклад.
Знайти
координати центра ваги тіла, обмеженого
поверхнями
,
![]() ,
,
,
.
,
,
,
.
Розв’язування.
Припустимо,
що маса рівномірно розподілена в об’ємі
тіла
,
тобто
![]() .
Тоді, враховуючи формули (2.10), (2.11) і
(2.12), маємо:
.
Тоді, враховуючи формули (2.10), (2.11) і
(2.12), маємо:
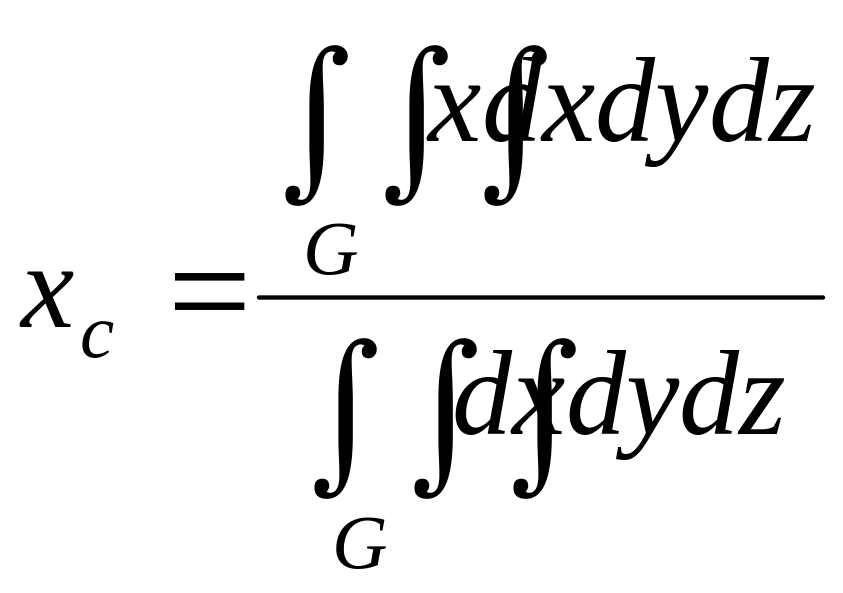 ;
;
Обчислення за цією формулою дає:
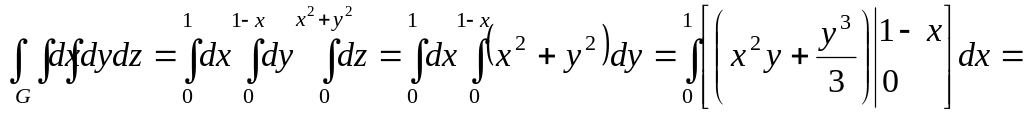
![]()
![]() .
.
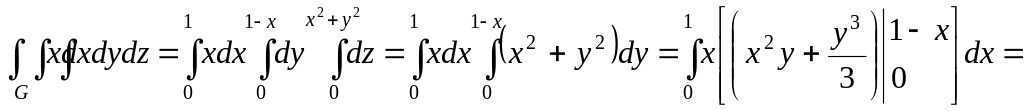
![]()
![]()
![]() ;
;
![]() .
.
Далі маємо:
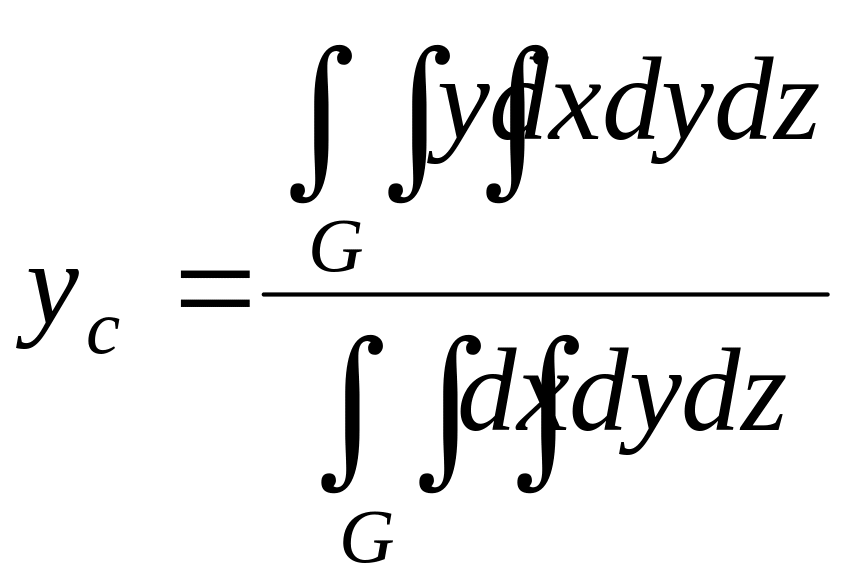 ;
;
Обчислення за цією формулою дає:
![]() ,
,
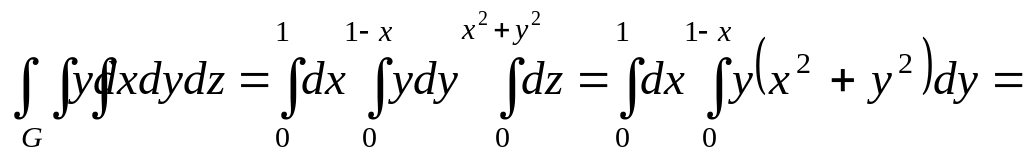
![]() ;
;
![]() .
.
Далі маємо:
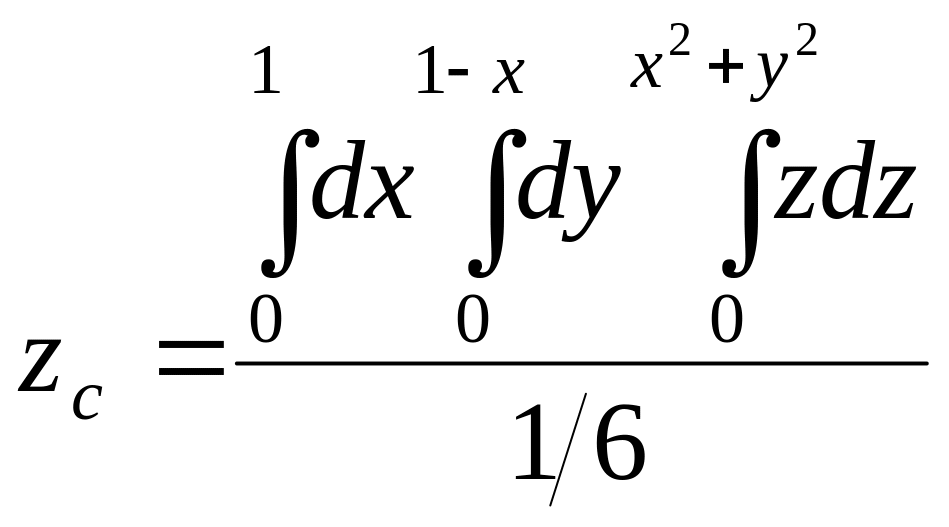 ,
,
Обчислення за цією формулою дає:
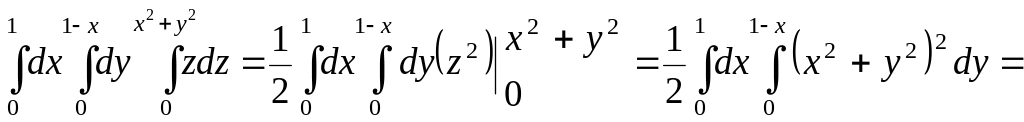
![]()
![]()
![]() ,
,
![]() .
.
Приклад.
Знайти
момент інерції однорідного за масою
![]() куба;
куба;
![]() ,
,
![]() ,
,
![]() ,
відносно його ребра.
,
відносно його ребра.
Розв’язування.
Використовуємо
формулу (2.13), в якій приймаємо
![]() .
Маємо:
.
Маємо:
![]()
![]() .
.
![]() .
.
] Частина ііі. Завдання для самостійної роботи
3.1. Варіанти завдань а), б), в)
Для самостійної роботи з подвійних інтегралів
а) |
Здійснити зміну порядку інтегрування в заданому подвійному інтегралі. |
б) |
За допомогою
формули
|
в) |
Обчислити
координати центра ваги однорідної
|
1. |
а) |
|
б) |
|
|
в) |
|
2. |
а) |
|
б) |
|
|
в) |
|
3. |
а) |
|
б) |
|
|
в) |
|
4. |
а) |
|
б) |
|
|
в) |
|
5. |
а) |
|
б) |
|
|
в) |
|
6. |
а) |
|
б) |
|
|
в) |
|
7. |
а) |
|
б) |
|
|
в) |
|
8. |
а) |
|
б) |
|
|
в) |
|
9. |
а) |
|
б) |
|
|
в) |
|
10. |
а) |
|
б) |
|
|
в) |
|
11. |
а) |
|
б) |
|
|
в) |
|
12. |
а) |
|
б) |
|
|
в) |
; |
13. |
а) |
|
б) |
|
|
в) |
|
14. |
а) |
|
б) |
|
|
в) |
|
15. |
а) |
|
б) |
|
|
в) |
|
16. |
а) |
|
б) |
|
|
в) |
|
|
17. |
а) |
|
б) |
|
|
в) |
|
18. |
а) |
|
б) |
|
|
в) |
|
19. |
а) |
|
б) |
|
|
в) |
|
20. |
а) |
|
б) |
|
|
в) |
|
21. |
а) |
|
б) |
|
|
в) |
|
22. |
а) |
|
б) |
,
|
|
в) |
|
23. |
а) |
|
б) |
|
|
в) |
|
24. |
а) |
|
б) |
|
|
в) |
|
25. |
а) |
|
б) |
,
|
|
в) |
|
26. |
а) |
|
б) |
,
|
|
в) |
|
27. |
а) |
|
б) |
,
|
|
в) |
|
28. |
а) |
|
б) |
|
|
в) |
|
29. |
а) |
|
б) |
|
|
в) |
|
30. |
а) |
|
б) |
|
|
в) |
|

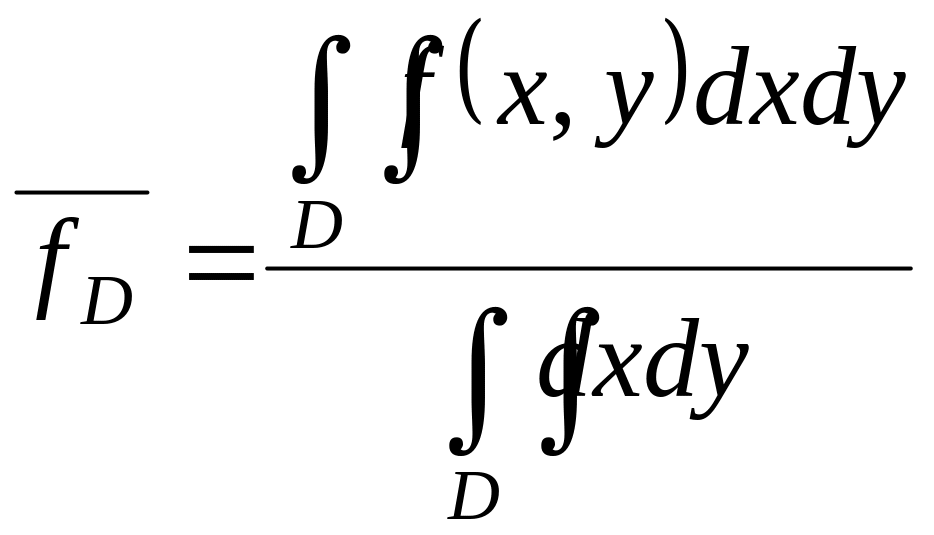 обчислити середнє значення
обчислити середнє значення