3. Обчислення подвійних інтегралів в полярних координатах

Перетворення подвійного інтеграла в прямокутних декартових координатах до інтеграла в полярних координатах , , які пов’язані з прямокутними координатами співвідношеннями

, ,

здійснюється за формулою

(1.9)

.

Якщо область обмежена променями, які утворюють з полярною віссю кути і , і кривими і , то відповідні полярні координати змінюються в межах , і тоді

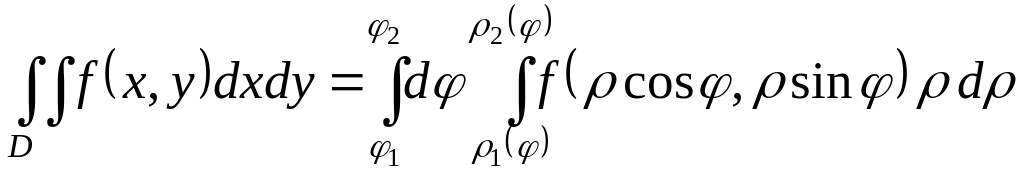. (1.10)

Якщо ж область охоплює початок координат, то

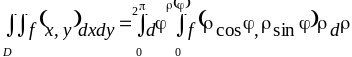, (1.11)

де – полярнt рівняння кривої, яка обмежує область .

Приклад.

Обчислити , де – область, обмежена кривою. .

Розв’язування. Рівняння кривої в полярних координатах записується . Тоді за формулою (1.10) маємо:

.

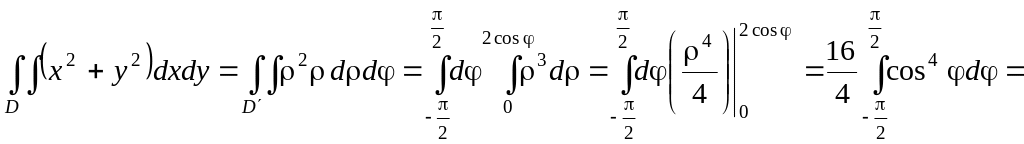
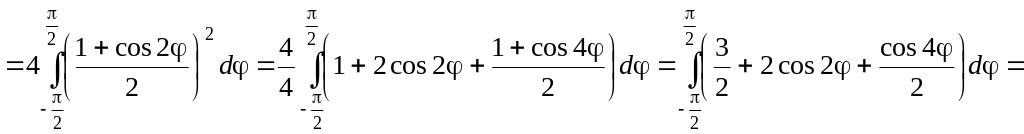
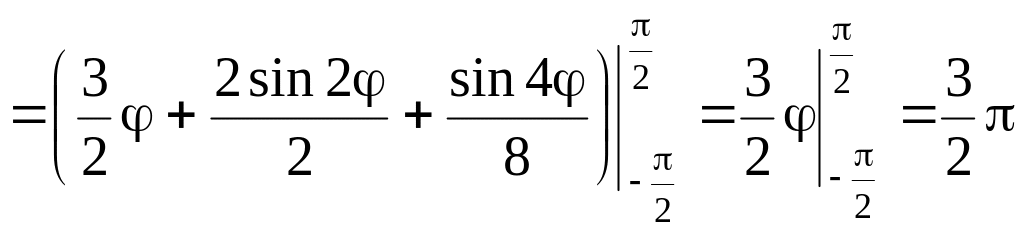3. Застосування подвійних інтегралів для обчислення площ плоских фігур, об’ємів циліндроїдів та площ поверхонь

а) Площа плоскої фігури, обмеженої областю , виражається формулою

,

Якщо область визначена, наприклад, нерівностями , , то

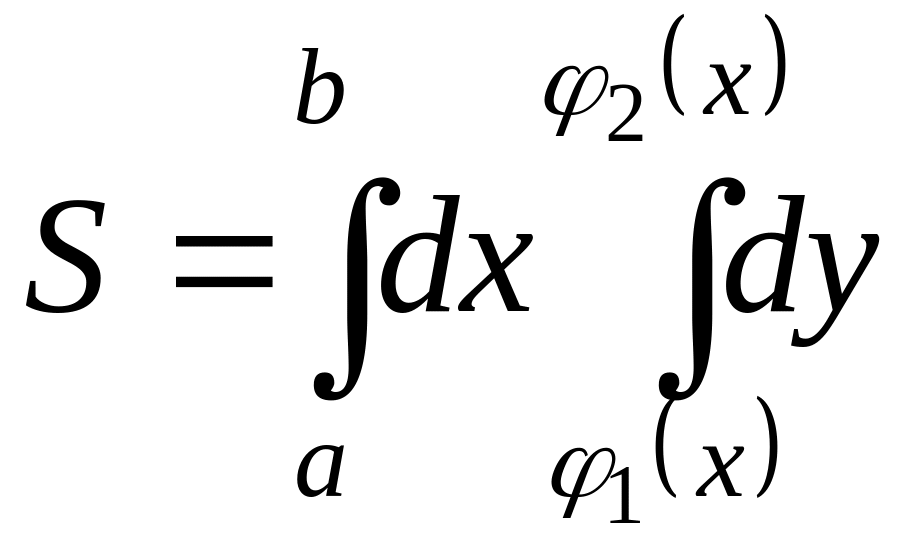(1.12)

Якщо область в полярних координатах визначена нерівностями , , то

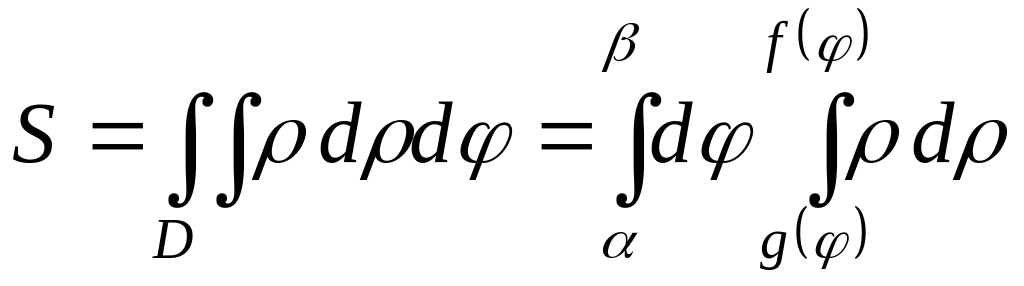(1.13)

Приклад.

Обчислити площу фігури, обмеженої колом радіуса .

Розв’язування. За формулою (1.13) маємо:

.

б) Об’єм циліндричного тіла, обмеженого зверху неперервною поверхнею , знизу – площиною і з боків – прямою циліндричною поверхнею, що вирізає на площині область , обчислюється за формулою

. (1.14)

Приклад.

Обчислити об’єм тіла, обмеженого поверхнями , , , і розташованого в 1 октанті.

Розв’язування. Це тіло обмежене зверху поверхнею , з боків – параболічним циліндром і площиною . Значить, воно є циліндричним тілом. Область обмежена параболою і прямими і . За формулою (1.14) маємо:

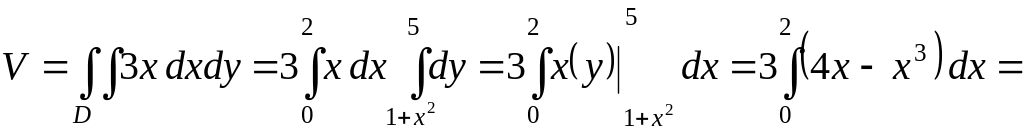
(од.)³.

в) Площа поверхні, яка задана рівнянням , виражається формулою:

, (1.15)

де – проекція даної поверхні на площину .

У випадку, коли – проекція поверхні на площину , то

.

Якщо – проекція поверхні на площину , то

Приклад.

Обчислити площу сфери радіуса .

Розв’язування. Хай центр сфери знаходиться в початку координат; тоді її рівняння буде . Будемо обчислювати площу ділянки, розташованої в 1 октанті. Тоді

; .

За формулою . Переходимо до полярних координат:

,

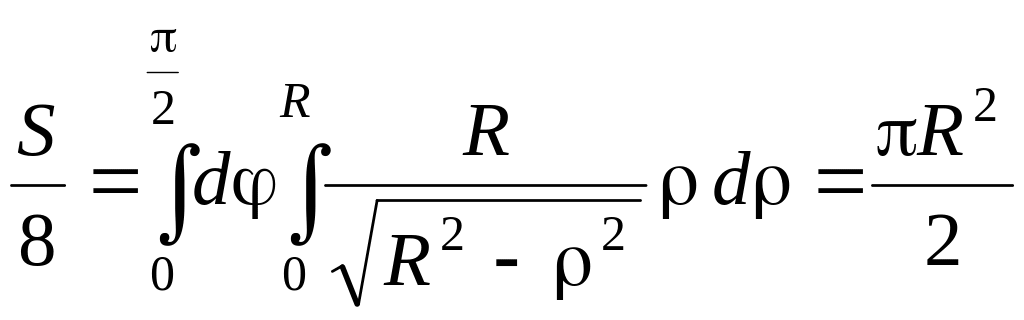звідки

.

3. Застосування подвійних інтегралів для обчислення маси, статичних моментів і моментів інерції та координат центра ваги плоских фігур

Якщо пластинка займає область площини і має змінну поверхневу густину , то маса пластинки виражається подвійним інтегралом

(1.16)

Статичні моменти і фігури відносно координатних вісей і обчислюються за формулами:

, (1.17)

Координати центра ваги обчислюються за формулами:

; (1.18)

Моменти інерції , відносно координатних вісей , і момент інерції відносно початку координат – відповідно за формулами [6]:

,

(1.19)

Приклад.

Знайти координати центра ваги пластинки, обмеженої параболою і прямою , якщо густина розподілу маси в кожній точці дорівнює ординаті цієї точки.

Розв’язування. Спочатку знайдемо масу пластинки. Тому що , то за формулою (1.16) одержимо:

.

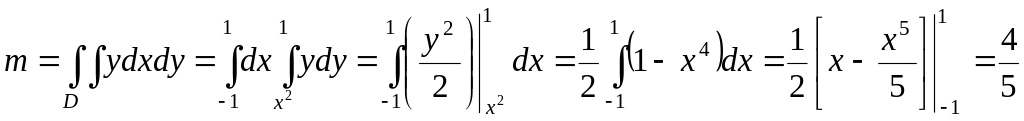Далі, за формулами (1.17) ,знаходимо і :

;

.

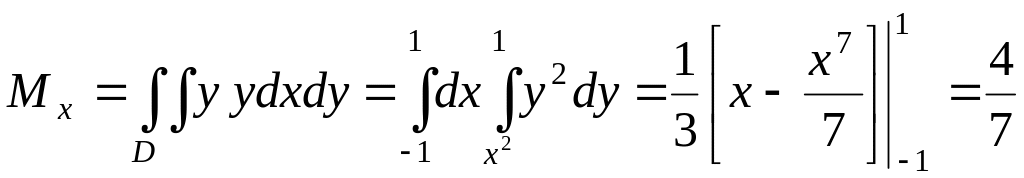Тому за формулами (1.18) маємо:

, .

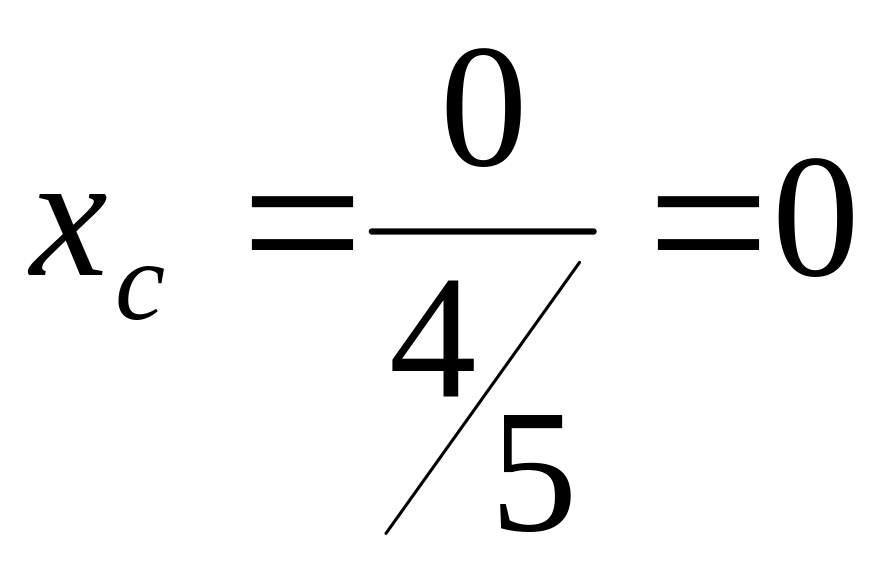Приклад.

Обчислити момент інерції однорідного квадрата зі стороною, рівною , відносно однієї із його сторін.

Розв’язування. Сумістимо початок координат з однією із вершин квадрата, а координатні вісі і направимо вздовж його сторін, які, очевидно, виходять із цієї вершини. Тоді шуканий момент інерції можна знайти за формулою . Тому що , то

.