1.7.3. Реализация схемы на дробных шагах
Рассматривается система (2).
На первом дробном шаге вид оператора диагональный, поэтому вектор потока для каждой своей координаты находится независимо от других координат.
если взять
,
то это неявная схема бегущего счета.
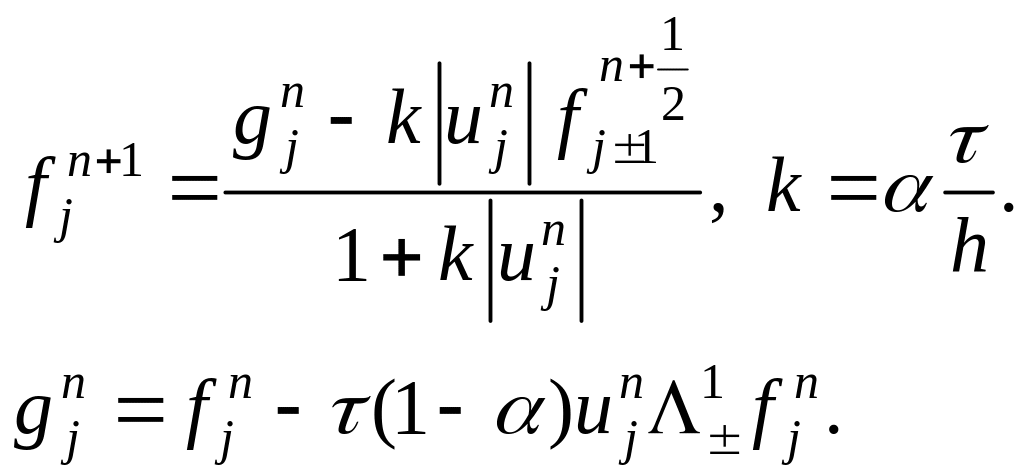
Если
,
то счет слева направо, если
– наоборот.
Если знак скорости меняется, то – 3-х точечная прогонка.
,
где 
.
Прогонка хорошо обусловлена при .
При
прогонка обусловлена при
.
В
случае плохой обусловленности
решаем методом немонотонной прогонки
.
.
Вводим фиктивный слой.
Можно использовать экстраполяционные формулы
,
или можно изменить аппроксимацию на границе на симметричную. В этом случае нарушается однородность разностной схемы.
На втором дробном шаге схемы (2) решается следующее уравнение:
В уравнении движения слагаемые с давлением аппроксимируются симметричным разностным оператором.
Исключаем
и
из последнего уравнения. Получаем
разностные уравнения для значения
скорости на
временном слое. Это уравнение решается
трехточечной скалярной прогонкой. Затем
из первых двух уравнений находятся
плотность и энергия.
Рассматривается схема (2):
Проверим устойчивость в линейном случае для схемы с замороженными коэффициентами.
.
На первом дробном шаге:
.
Заменим
для удобства
.
Выпишем определитель.
Если
,
то определитель имеет вид:
.
при
.
Вместо
можно взять
,
так как эти коэффициенты не меняются.
На
втором дробном шаге сразу выпишем корни
характеристического уравнения
(задействована матрица
,
которая не является диагональной).
,
где
– скорость звука:
.
,
где
при
;
при
.
,
при
.
1.7.4. Уравнения газовой динамики и Навье-Стокса в переменных, полученных комбинацией газодинамических переменных
При построении газодинамических схем в качестве переменных могут быть выбраны различные комбинации газодинамических параметров.
Один
из вариантов:
.
Выбор таких переменных обусловлен следующим:
Уравнения газовой динамики и Навье-Стокса в этих переменных имеют более простую форму и просты в реализации.
Уравнения неразрывности и движения записываются в дивергентной форме. А это приводит к ускорению сходимости схемы к стационарному решению.
Уравнение энергии может быть использовано как и в недивергентной, так и в дивергентной форме. При использовании уравнения энергии в дивергентной форме мы получаем полностью консервативные схемы (т.е выполняются все законы сохранения).
Рассмотрим систему:
, (1)
где для случая системы газовой динамики:
,
а для случая системы уравнений Навье-Стокса:
.
Здесь
.
Рассмотрим разностную схему для системы уравнений газовой динамики:
. (2)
.
Схема
нелинейна относительно
.
Проводим линеаризацию:
.
(2)
,
где
.
Для
того, чтобы получить оператор
,
который удовлетворяет следующим
требованиям:
Схема должна остаться безусловно устойчивой.
Реализована скалярными прогонками.
Требовать минимального числа операций.
Матрицу
можно расщепить четырьмя способами, но
для выполнения третьего условия,
расщепляем так:
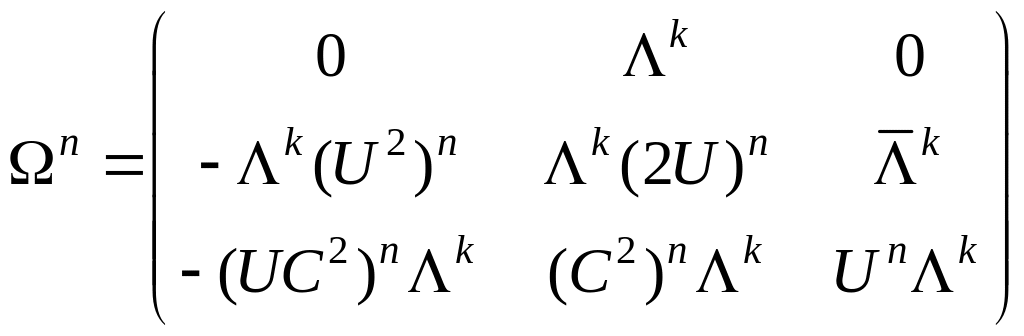расщепляется
на:
.
.
Окончательно имеем:
.
Данная схема может быть реализована с помощью дробных шагов. Можно использовать метод «стабилизирующей поправки».
(4)
Реализация схемы (2) в зависимости от расщепляющих операторов следующая:
На первом дробном шаге матрица нижнетреугольная (
),
поэтому переменные находятся так:
сначала
.
А затем независимо друг от друга находят
и
.На втором дробном шаге получили систему:
Из последнего уравнения выражается и подставляем во второе. Получаем уравнение, которое решается скалярными прогонками. А затем пересчитываются первое и третье уравнения.
В качестве уравнения энергии выбираем уравнение в дивергентном виде:
.
,
где
.
– уравнение
связи.
Для решения системы используем следующую схему с весами, которая аппроксимирует исходную систему с , но является нелинейной относительного верхнего временного слоя:
.
Для получения линейной системы проводим линеаризацию, используя следующие разложения в ряд Тейлора:
.
.
.
.
Подставляем эти выражения, получаем линеаризованную схему:
. (3)
Эта система может быть решена векторными прогонками. Для того, чтобы получить систему, реализующуюся скалярными прогонками, проводим расщепление и рассматриваем схему с факторизованным стабилизирующим оператором или рассматриваем схему в дробных шагах, эквивалентную ей.
. (4)
В этом случае схема (3) имеет вид:
,
где
.
и
порядок аппроксимации
.
Схема реализуется в дробных шагах.
(5)
.
На первом дробном шаге:
На втором дробном шаге:
Расщепление
матрицы
на матрицы
и
неоднозначно. Можно выбрать такое:
.
Схемы при таком расщеплении на каждом дробном шаге реализуются по схемам бегущего счета. Но схема становится условно устойчивой.