1.6.1. Схемы приближенной факторизации

Эти схемы эквивалентны схемам в дробных шагах до второго порядка точности по времени.

Рассмотрим схему с весами для уравнений газовой динамики:

Перейдем к канонической форме:

.

.

,где .

Данная схема является экономичной.

На первом шаге решаются две независимые системы уравнений. При этом, найден из начальных условий.

Схема безусловно устойчива, и уравнение устойчивости имеет вид:

.

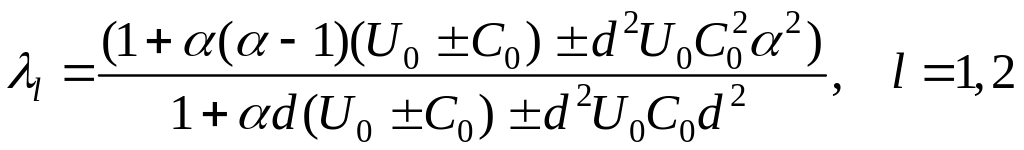, при

Рассмотренные схемы в дробных шагах и приближение факторизации можно обобщить на полную систему уравнений газовой динамики и на систему уравнений Навье-Стокса, не теряя при этом устойчивости схемы и порядок аппроксимации.

Схема для одномерных уравнений газовой динамики в дивергентной форме:

, (1)

где .

. (2)

Погрешность (2): .

Чтобы строить безытерационные схемы, линеаризуем схему относительно верхнего временного слоя.

,

где .

Подставляя в (2), имеем:

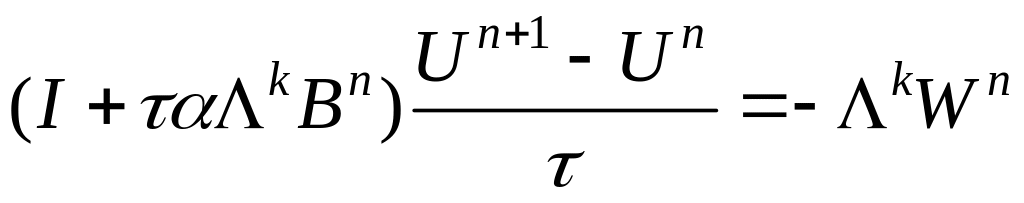. (3)

Уравнение (3) решается векторными прогонками со следующими коэффициентами (при имеем симметричную аппроксимацию):

.

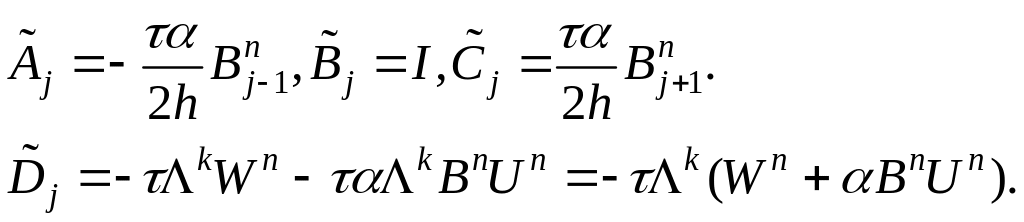
Попытаемся выписать матрицу для идеального газа.

Уравнение Менделеева- Клапейрона:

.

.

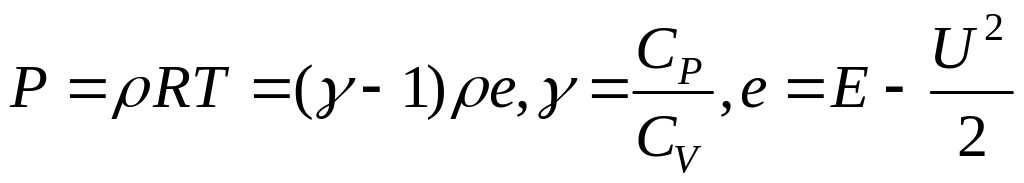В итоге получаем следующую матрицу :

.

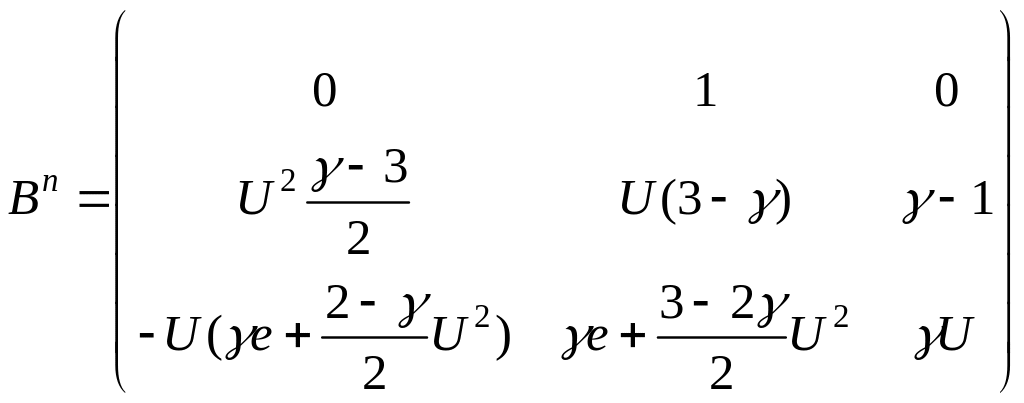коэффициенты устойчивости следующие:

1.7. Разностные схемы для полной системы уравнений Навье-Стокса

Построим для этой системы разностную схему с весами:

, (4)

где .

Замечание: появляются вторые производные по пространству.

. (2)

.

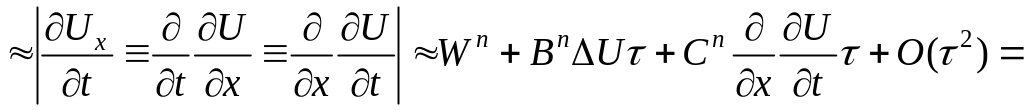
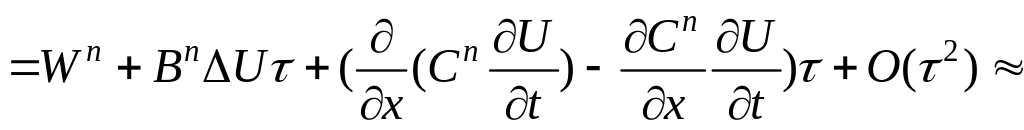
Подставляем в уравнение:

. (5)

Вид матриц можно упростить, если в качестве искомых переменных выбирать не вектор состояния в массовых переменных, а вектор и т. д. В этом случае легче ставятся граничные условия. Уменьшается число арифметических операций. В этом случае канонический вид разностной схемы подобен уравнению (5), но теперь уже:

.

1.7.1. Понятие о монотонных разностных схемах

Разностные схемы при (не)симметричных аппроксимациях не обладают свойствами монотонности. Поэтому при расчете разрывных течениях происходят осцилляции на разрывах и надо проводить сглаживание.

Так как система уравнений газовой динамики обладает свойством гиперболичности, то она невырожденными преобразованиями может быть приведена к симметричному виду.

.

1. Система уравнений газовой динамики является однородной.

.

Возьмем матрицу диагонального вида

Система Маккормака в этом случае:

,

где

1.7.2. Схемы для одномерных уравнений в недивергентной форме

Уравнения газовой динамики и уравнения Навье-Стокса могут использовать несколько форм представления:

1. Дивергентная.

2. Недивергентная.

3. Предельная дивергентная.

Мы рассмотрели различные виды разностных схем в дивергентной форме. Было подчеркнуто, что в результате линеаризации этих уравнений получены сложные матрицы B и С. Поэтому предлагается выбор исходного вектора переменных в эквивалентной форме, благодаря которому можно получить более экономичную разностную схему. Как правило, для уравнений газовой динамики выбирается в переменных , что позволяет решать независимо уравнение неразрывности относительно остальных уравнений системы. Для системы уравнений Навье-Стокса выбирается в переменных , что позволяет аккуратно записывать граничные условия.

Уравнения газовой динамики:

. (1)

.

Уравнения Навье-Стокса:

. (2)

.

.

Для решения этих уравнений предлагается следующая разностная схема:

(3)

Схема (3) аппроксимирует (1) и (2) с , где зависит от порядка разностной производной. Для уравнений газовой динамики

.

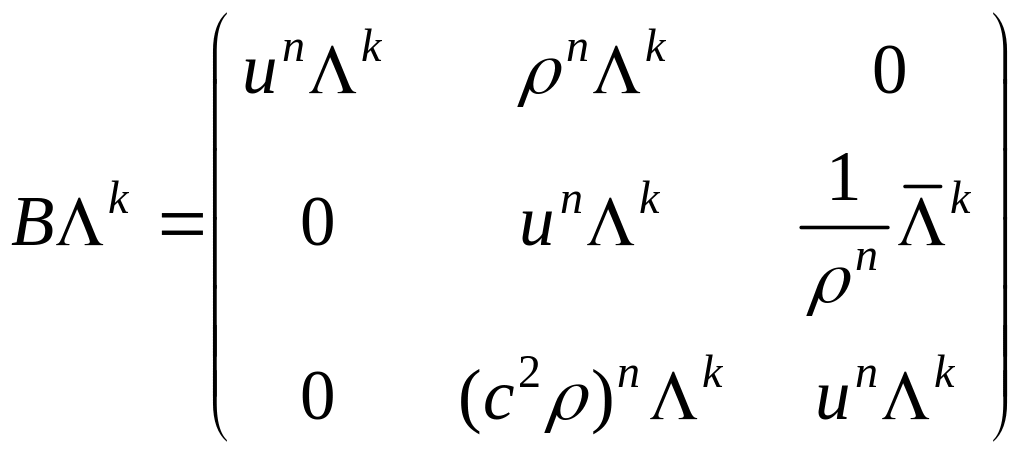и для уравнений Навье- стокса

– для получения безусловно устойчивой схемы.

Из вида матриц и (3) видно, что для нахождения решения (2) используется векторные прогонки, а для решения (1) используются векторная прогонка для нахождения координат и , а затем можно пересчитать из уравнения неразрывности методом сквозного счета.

Схема (3) безусловно устойчива при .

Выведем условие устойчивости для схемы (3) в случае решения системы газовой динамики (1), выбирая симметричную аппроксимацию пространственных переменных ( ).

.

.

.

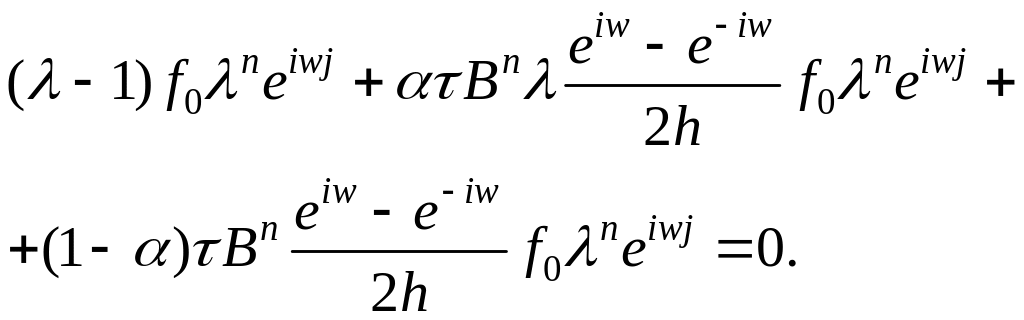
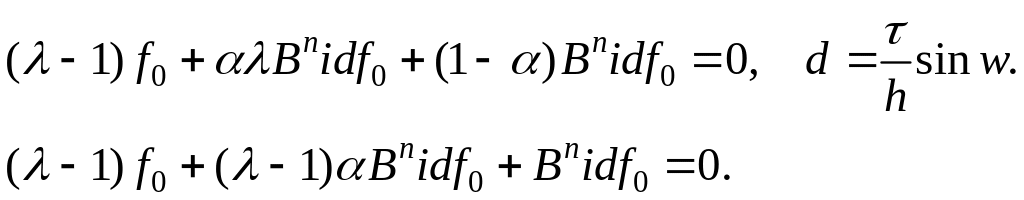
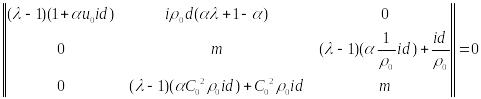
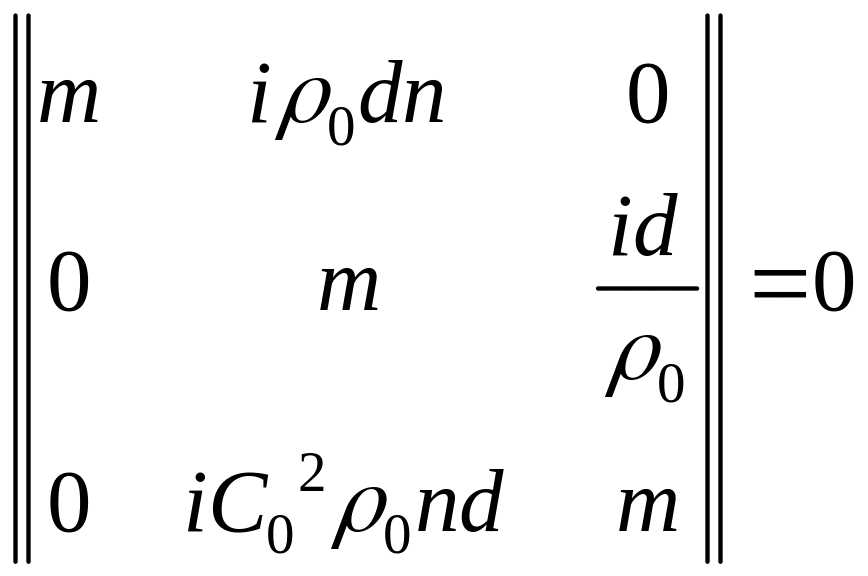Схема безусловно устойчива при .

Для получения схем, реализующихся скалярными прогонками, можно какие-то из слагаемых, например с , аппроксимировать на нижнем временном слое, но при этом ухудшается условие устойчивости – схемы становятся условно устойчивыми и условие устойчивости зависит от числа Маха:

– число Маха.

Например, система уравнений газовой динамики имеет вид

В качестве модельной, выберем систему уравнений газовой динамики в переменных :

Система (1) недивергентного вида и давление исключено из этой системы с помощью уравнения состояния:

.

Используем расщепление дифференциального оператора по физическим процессам:

Оператор учитывает конвективные слагаемые. Оператор учитывает слагаемые при градиенте давления в уравнении скорости и слагаемые при градиенте скорости в уравнении неразрывности и движения.

Уравнение (1) после расщепления примет вид:

(2)

(2) – схема с весами по пространству, является схемой слабой аппроксимации.

Перепишем схему (2), выделяя стабилизирующие операторы:

Выразим в целых временных шагах. Для этого первое уравнение умножим слева а второе на и сложим оба уравнения:

Операторы и в общем случае неперестановочные. В частном случае, когда и когда их можно убрать, эти операторы можно менять местами.

Таким образом схема (2) имеет первый порядок по времени и -й по пространству в общем нелинейном случае.

Если и в случае уравнения с постоянными коэффициентами оно имеет 2-й порядок аппроксимации по времени.