1.4.4. Разностные схемы с весами

Рассмотрим уравнение (2)

. (2)

Для его численной реализации используем схему с весами

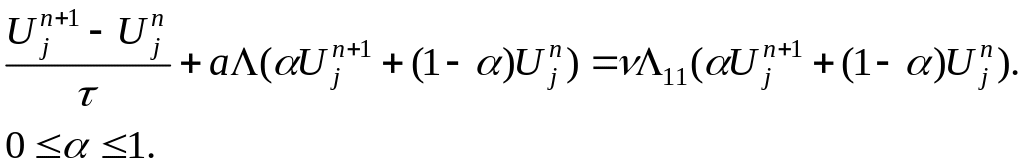
– схема явная.

– схема неявная.

Порядок аппроксимации: .

Когда , то , то есть порядок аппроксимации схемы .

При всех остальных – схема первого порядка. Расписывая более подробно разностное уравнение

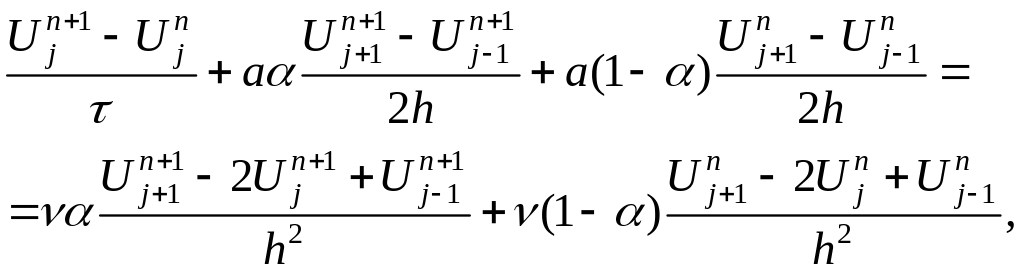
где

и преобразуя его к трехточечному виду получаем:

.

В нашем случае прогоночные коэффициенты:

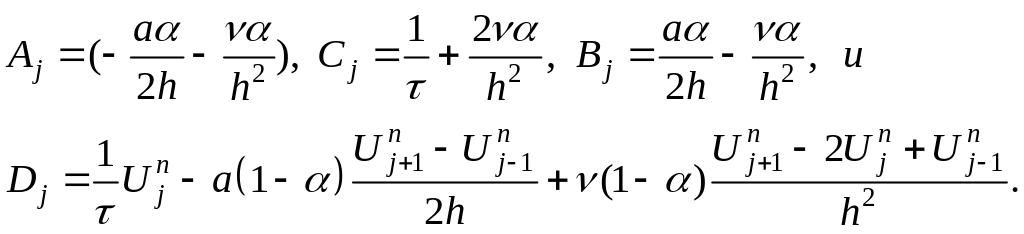
Достаточное условие корректности и устойчивости метода прогонки (условие диагонального преобладания): , и одно из неравенств должно быть строгим.

В нашем случае, получим:

.

Рассмотрим только конвективные члены ( ):

– Получили даже в неявной схеме условие Куранта.

Чтобы избежать этого ограничения, необходимо аппроксимировать не центральными разностями, а односторонними.

Исследуем условие устойчивости схемы.

В прежних обозначениях имеем:

.

.

.

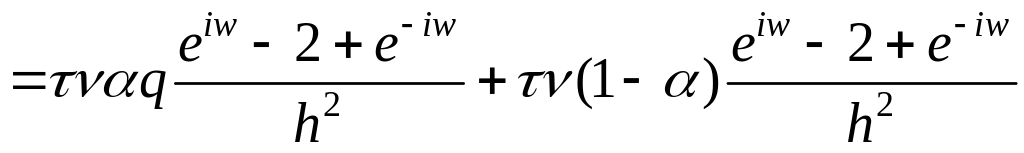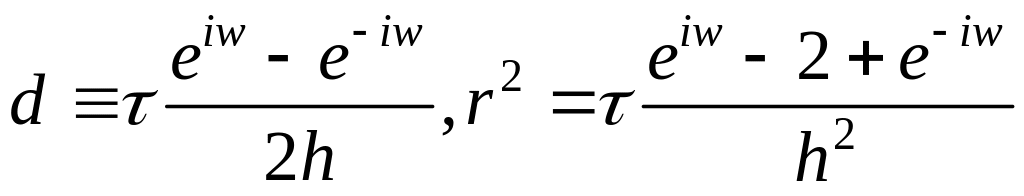При схема становится безусловно устойчивой.

1.4.5. Разностная схема с весами для нелинейных уравнений

Из уравнения

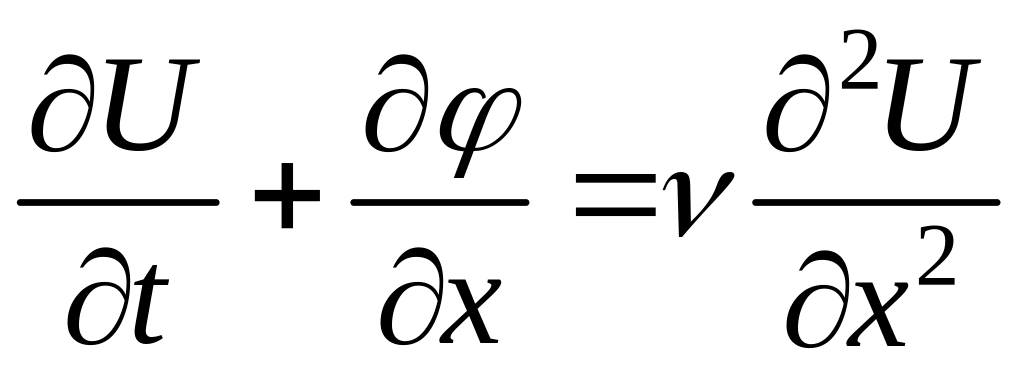(4)

.

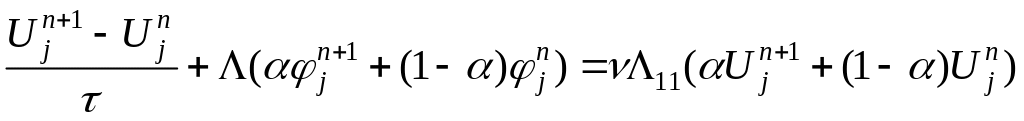Здесь метод прогонки использовать нельзя. Необходимо линеаризовать уравнение (или решать итерационными методами).

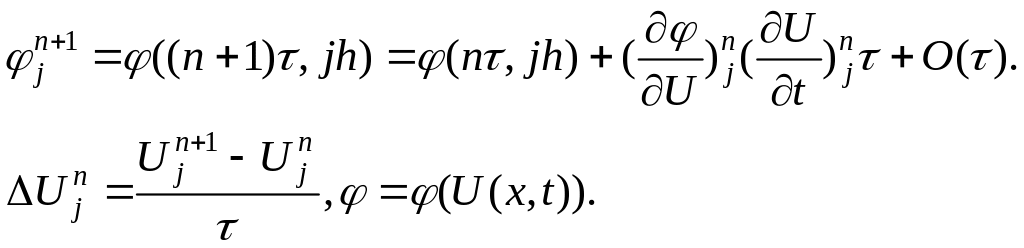
При линеаризации получим

.

В канонической форме это уравнение имеет вид:

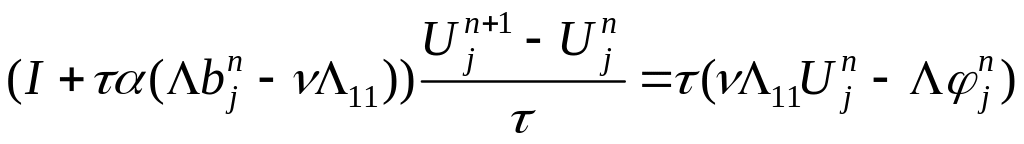
При схема безусловно устойчива.

Можно строить разностные схемы для нелинейных уравнений и на основе метода «предиктор-корректор».

1.4.6. Схема Маккормака для нелинейных уравнений

В этой схеме на этапе «предиктор» уравнение решается явно, а второе – неявно. Такие схемы называются схемами с несогласованной аппроксимацией (у которых уравнения имеют разный порядок аппроксимации). Как правило, первое уравнение имеет первый порядок аппроксимации, а второе – второй.

1.5. Методы построения схем повышенного порядка аппроксимации

Получение разностных схем повышенного порядка аппроксимации базируется на трех методах:

1. С помощью многосеточных методов.

2. С помощью выбора специального оператора усреднения (компактные схемы).

3. С помощью дифференциального приближения.

Рассмотрим второй метод:

. (1)

Интегрируем (1) на с помощью одного из численных методов (Симпсона, треугольников).

. (2)

Раскладываем и в ряд Тейлора до третьего порядка:

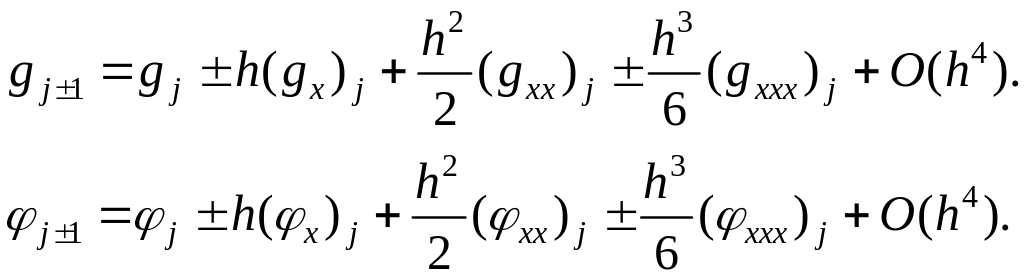(3)

Из (1)

(3) (2)

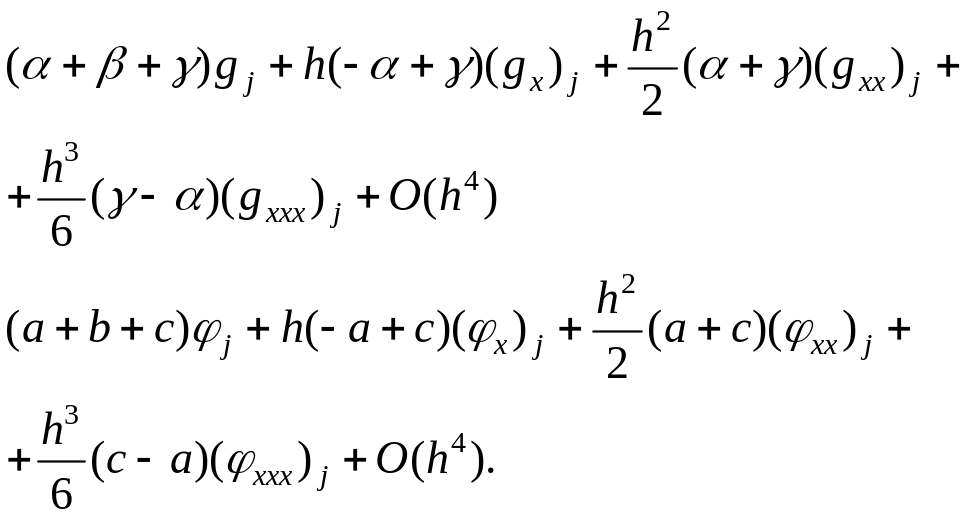
Получим систему уравнений для коэффициентов , используя (1):

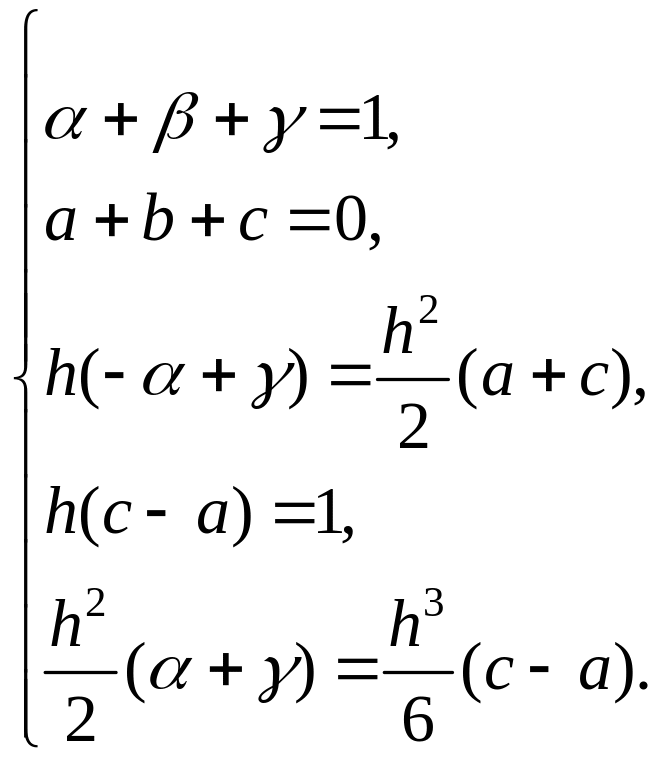
Решим полученную систему уравнений относительно параметра :

Таким образом, получаем:

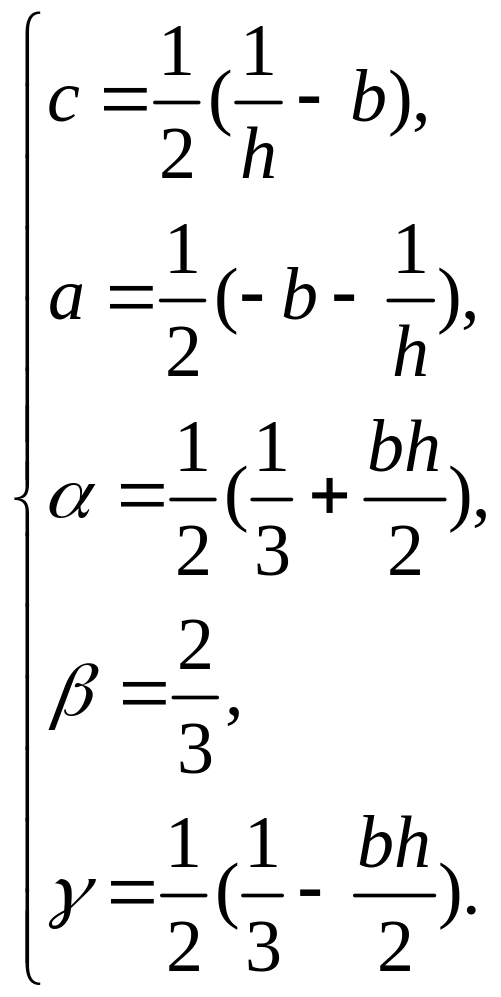
Подставим полученные значения в (2):

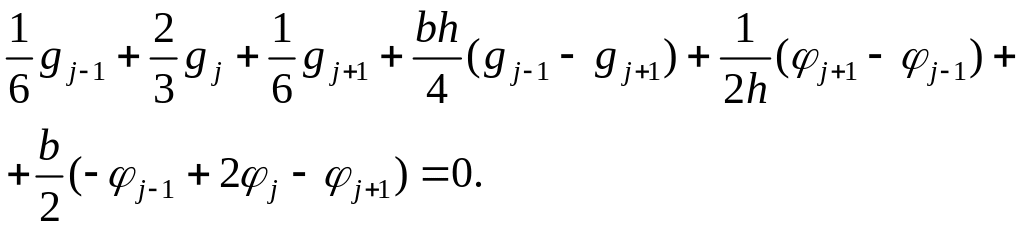
Получим однопараметрическое семейство разностных схем третьего порядка аппроксимации.

Чаще всего выбирается таким образом:

1. .

2. .

3. .

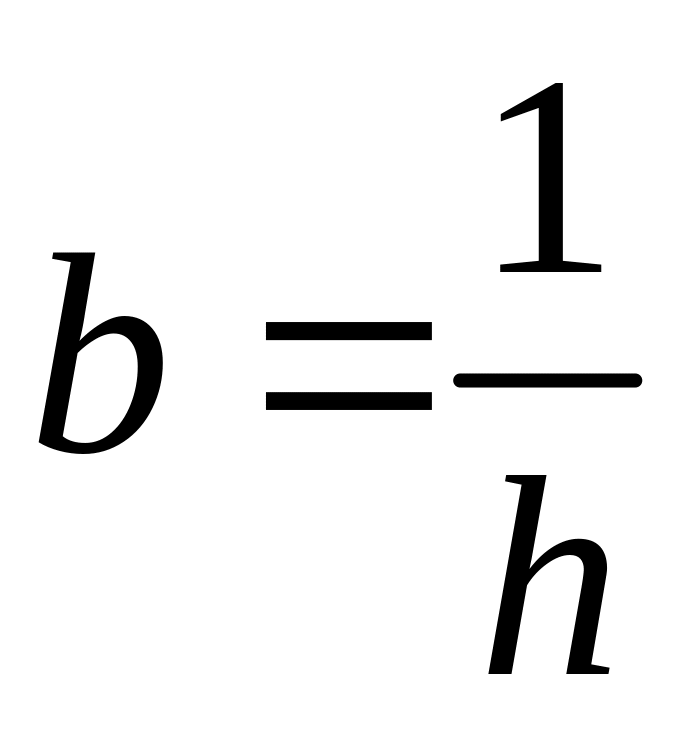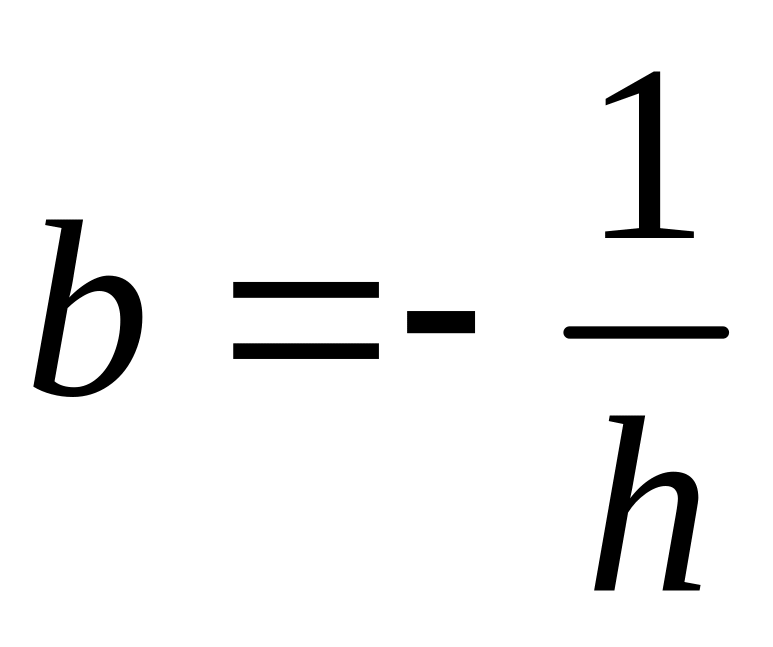Представим полученную схему в виде:

, – оператор усреднения.

Рассмотрим, что получится при :

.

При , имеем:

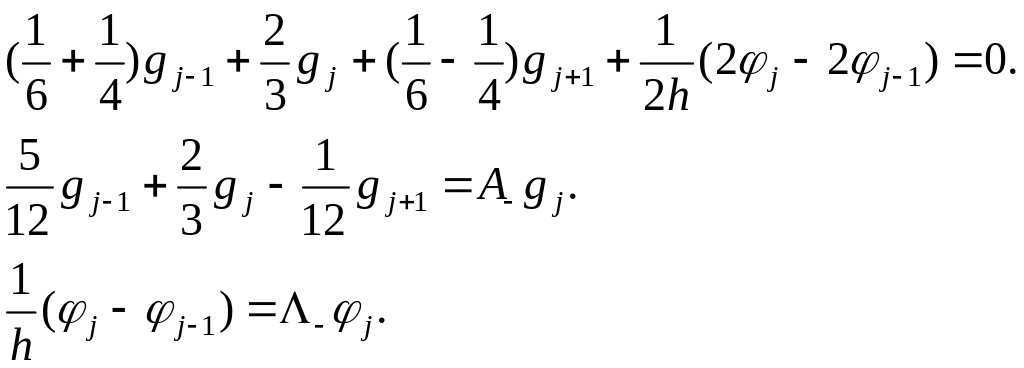
Для аналогично получим:

Рассмотрим уравнение:

.

.

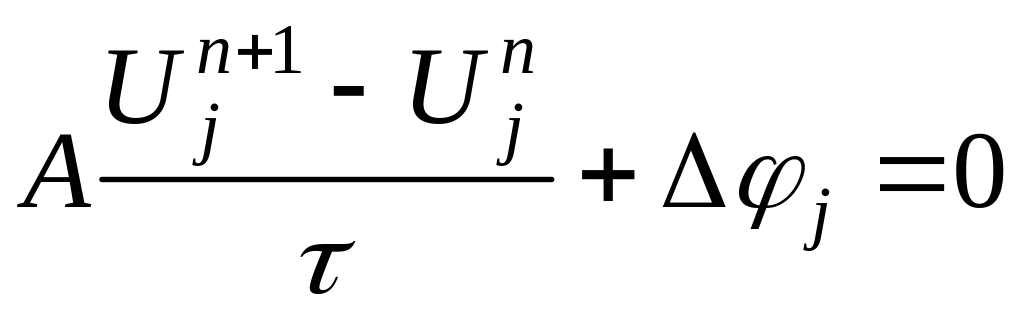Схема нелинейная и для исследования ее устойчивости необходима линеаризация. При этом порядок аппроксимации ухудшается.

Аппроксимировать можно и по времени и по пространству. Пример такой трехслойной схемы:

.

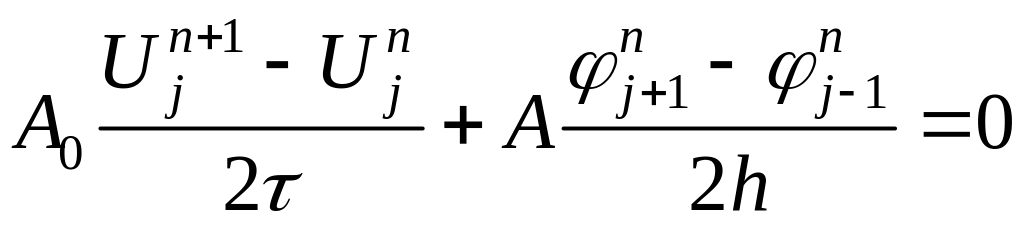На решение уравнения схема аппроксимирует исходную систему с . Схема условно устойчива.

1.5.1. Дисперсионные свойства разностных схем. Схема Лакса.

Решается уравнение

.

Условно устойчивая схема:

. (*)

Напишем дифференциальное приближение (раскладываем в ряд Тейлора до третьего порядка) в окрестности точки

.

Получили второе дифференциальное приближение для схемы (*). Далее подставляется гармоника (вносится искажение):

.

Затем составляем характеристическое уравнение и ищем параметр :

.

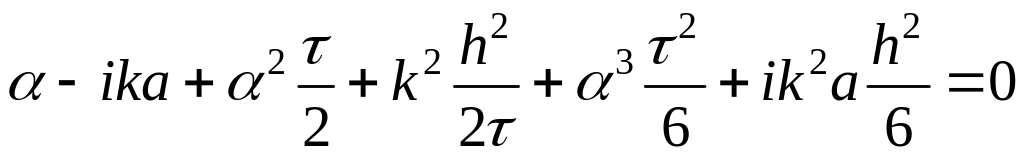Характеристическое уравнение для нахождения решается любым итерационным методом, в частности, методом последовательных приближений. Проделывается три последовательных итерации, получаем второй порядок аппроксимации и по времени, и по пространству:

Тогда имеем:

.

Коэффициенты диффузии:

.

– число Куранта

Коэффициенты дисперсии:

.

Коэффициенты сеточной диффузии для схемы Лакса могут быть большими.