
- •Модуль 2 Разностные методы решения задач прикладной механики
- •Комплексная цель модуля
- •Введение
- •Система уравнений движения вязкого сжимаемого теплопроводного газа
- •1.3.1. Безразмерные величины. Понятие критериев подобия
- •Задача. Течение в канале переменного сечения (сопла Лаваля). Рассматриваются одномерные течения совершенного газа, описанные системой:
- •1.3.2. Преобразования уравнений системы. Переход к недивергентной форме записи уравнений Навье-Стокса в различных исходных газодинамических переменных
- •1.3.3. Схемы расщепления по пространственным переменным и физическим процессам для уравнения недивергентной формы
- •1.3.4. Различные модельные уравнения, получающиеся из полной системы уравнений Навье-Стокса
- •1.3.5. Упрощенные модели систем уравнений Навье-Стокса. Теория пограничного слоя
- •1.3.6. Параболизированная система уравнений Навье-Стокса
- •1.3.7. Иллюстрация применимости моделей
- •1.3.8. Краевые условия для задач внешнего обтекания
- •1.4. Разностные схемы для модельных уравнений
- •1.4.3. Безусловно устойчивые разностные схемы
- •1.4.4. Разностные схемы с весами
- •1.4.5. Разностная схема с весами для нелинейных уравнений
- •1.4.6. Схема Маккормака для нелинейных уравнений
- •1.5. Методы построения схем повышенного порядка аппроксимации
- •1.6. Разностные схемы для системы уравнений газовой динамики
- •1.6.1. Схемы приближенной факторизации
- •1.7. Разностные схемы для полной системы уравнений Навье-Стокса
- •1.7.1. Понятие о монотонных разностных схемах
- •1.7.2. Схемы для одномерных уравнений в недивергентной форме
- •1.7.3. Реализация схемы на дробных шагах
- •1.7.5. Схемы с несогласованным стабилизирующим оператором
- •1.7.6. Схемы для решения стационарных задач
- •1.7.7. Схемы для многомерных уравнений
- •1.8. Заключение по модулю
- •1.9. Проектное задание
- •1.10. Тест рубежного контроля
- •Бланк правильных ответов
1.3.8. Краевые условия для задач внешнего обтекания
Рассматривается
в пространстве система непересекающихся
тел
![]() ,
которые могут как покоиться, так и
двигаться.
,
которые могут как покоиться, так и
двигаться.
![]() .
.
Тела ограниченны кусочно-непрерывными поверхностями:
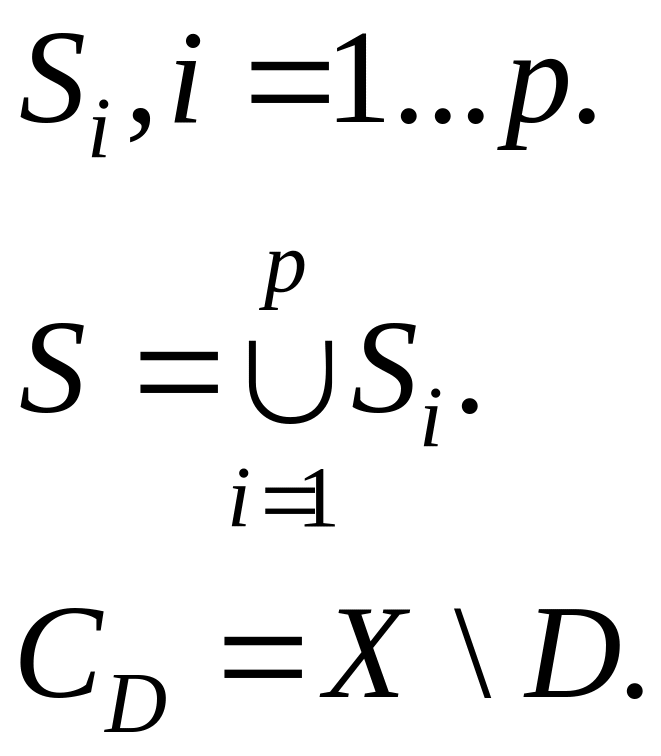
![]() – дополнение
пространства.
– дополнение
пространства.
В этом дополнении задано начальное состояние потока.
![]() .
.
И задается система:
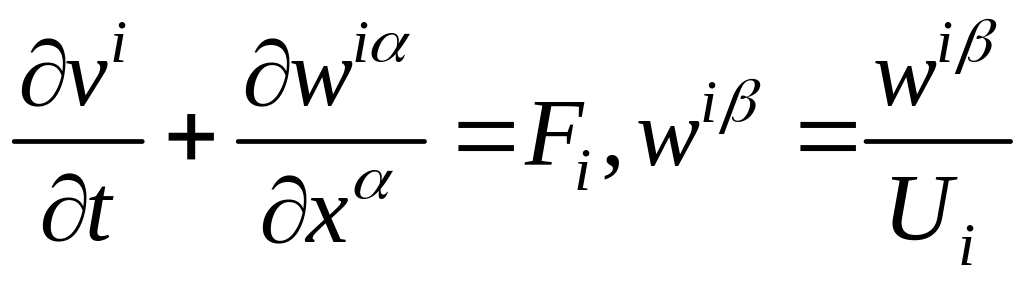
Ставятся следующие условия:
Условие равномерности потока на бесконечности.
![]() .
.
На границе тел , если учитывать вязкость (три механизма диссипации), ставится условие прилипания:
![]() ,
,
где
![]() – скорость
движения частиц вблизи поверхности,
– скорость
движения частиц вблизи поверхности,
![]() – скорость
движения поверхности.
– скорость
движения поверхности.
![]() -
где
-
где
![]() – скорость отсоса газа.
– скорость отсоса газа.
Для температуры
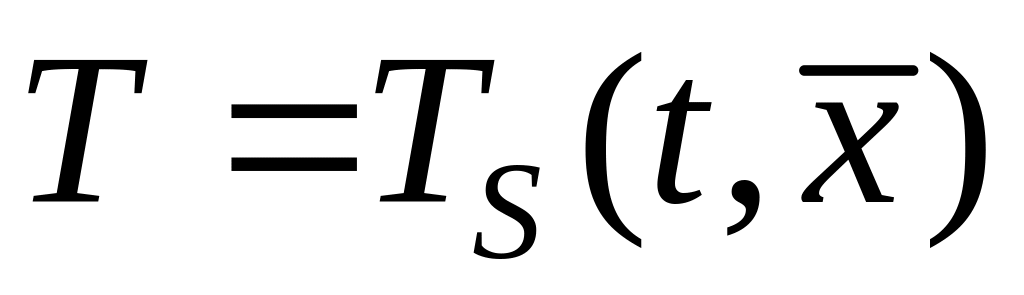
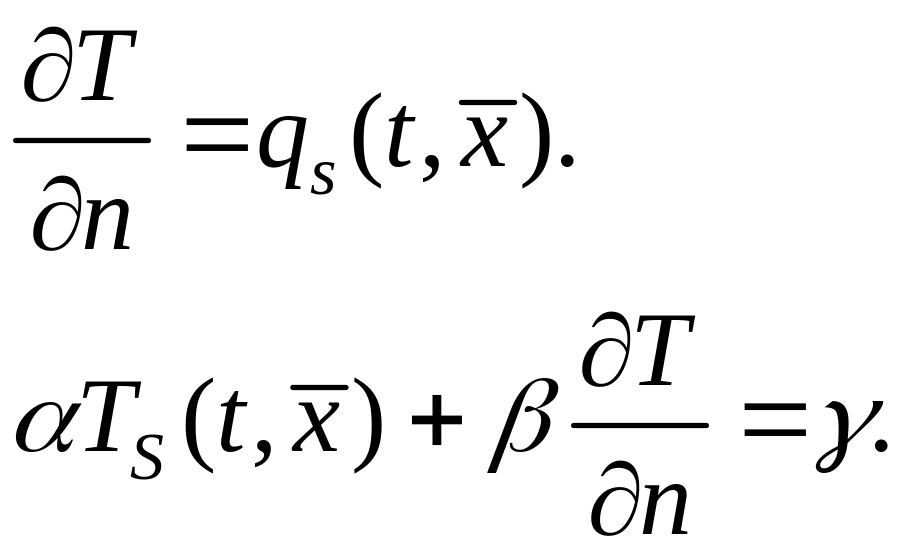 – более
сложное распределение, где
– более
сложное распределение, где
![]() .
.
Граничные условия на выходной границе:
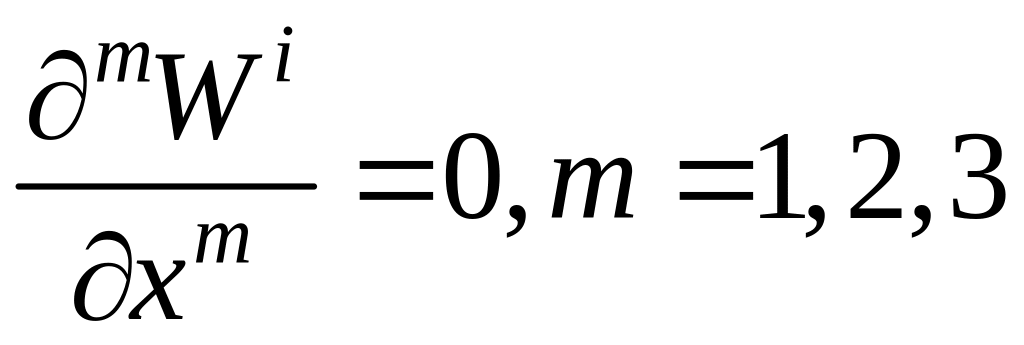 .
.
Это
мягкие граничные условия. В основном
берут
![]() .
.
1.4. Разностные схемы для модельных уравнений
1.4.1. Основные понятия теории разностных схем
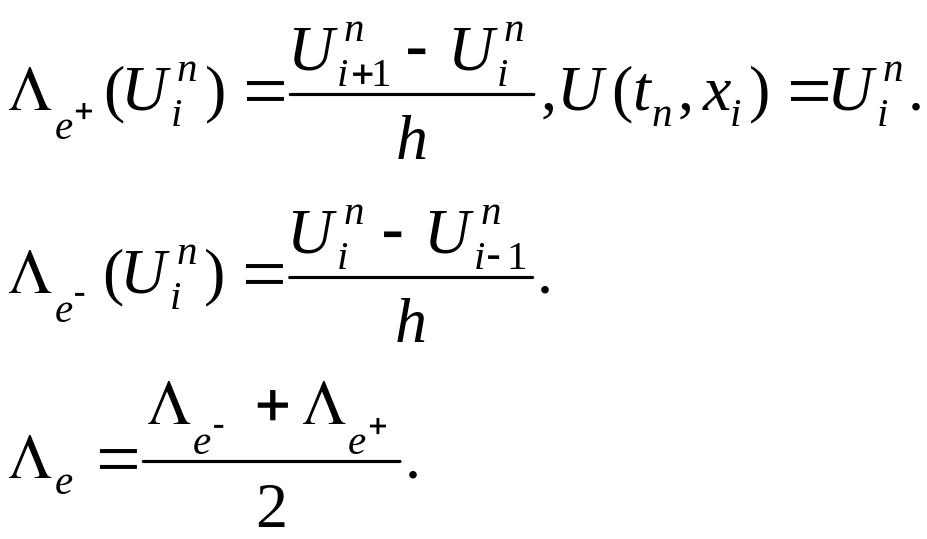
1.4.2. Рассмотрим модельные уравнения:
![]() . (1)
. (1)
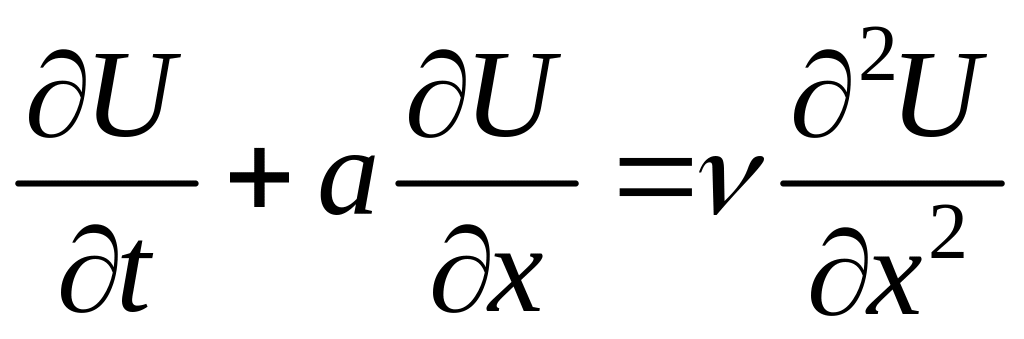 . (2)
. (2)
![]() . (3)
. (3)
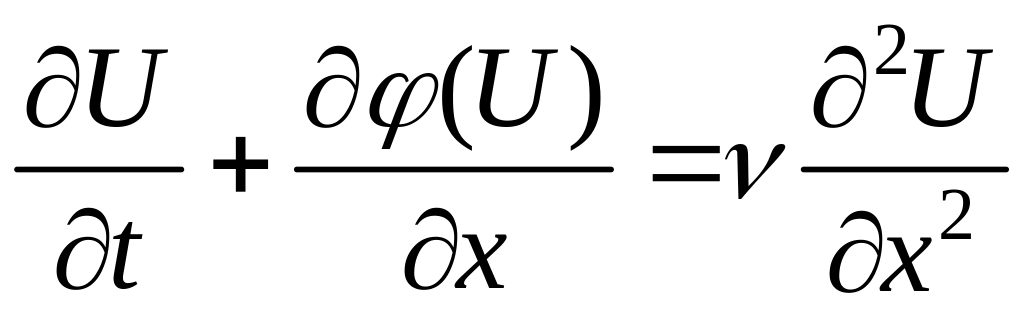 . (4)
. (4)
![]()
Исследуем на устойчивость явную схему для уравнения (1).
Пусть
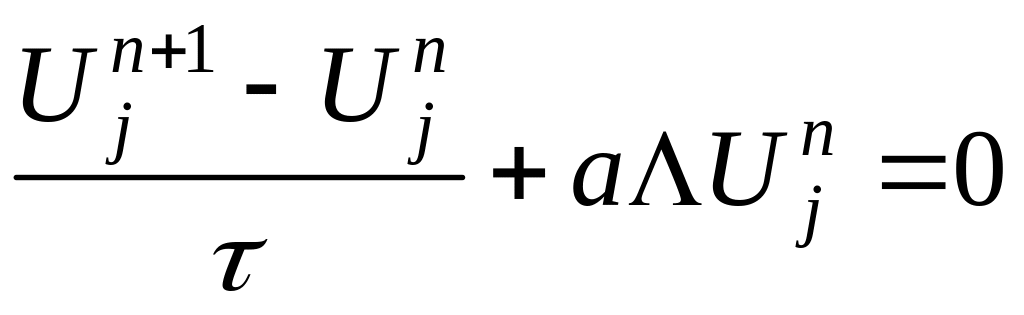 . Выбираем
гармонику (1.1)
. Выбираем
гармонику (1.1)
![]() ,
здесь
,
здесь
![]() .
.
 и
подставляем ее в уравнение.
и
подставляем ее в уравнение.
Тогда схема (1.1) примет вид:
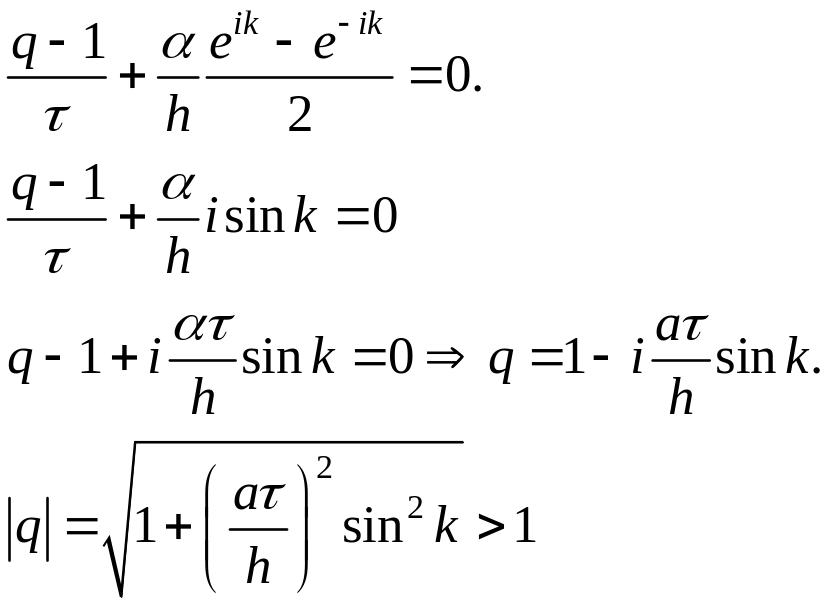
Схема неустойчива.
Для
того, чтобы схема стала устойчивой,
необходимо учитывать знак числа
![]() :
:
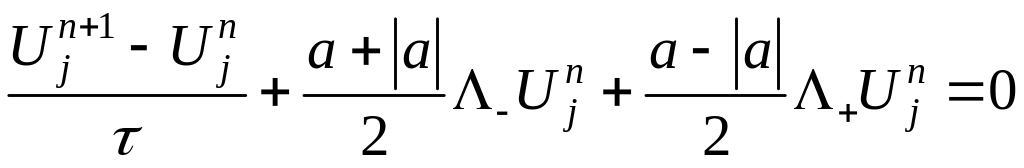 . (1.2)
. (1.2)
Аналогично, как и в предыдущем примере, получим
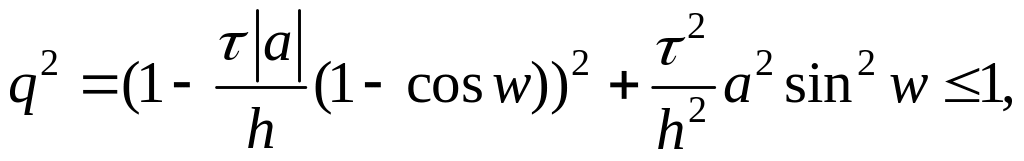
при выполнении условия Куранта-Фридрихса-Леви:
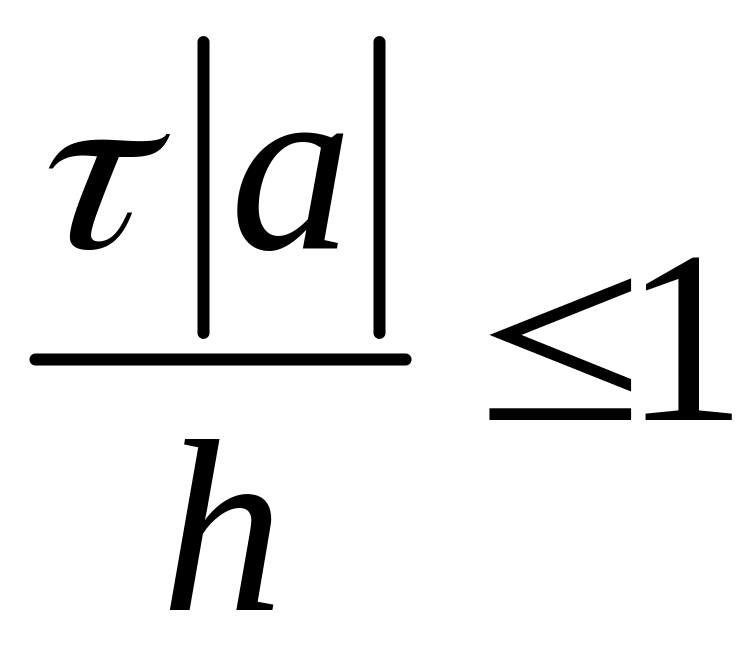 –(
класс условно устойчивых схем).
–(
класс условно устойчивых схем).
Рассмотрим
исходную схему
![]() ,
тогда ее можно преобразовать в следующую
схему Лакса:
,
тогда ее можно преобразовать в следующую
схему Лакса:
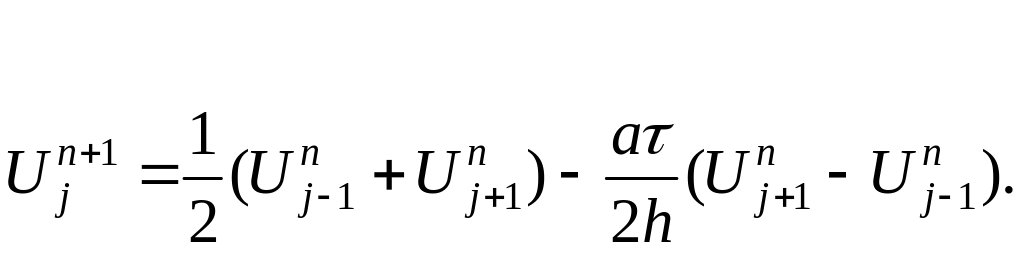 (1.3)
(1.3)
Схема (1.3) условно устойчива.
Для схемы (2) с диссипативным слагаемым, выпишем условно устойчивую схему:
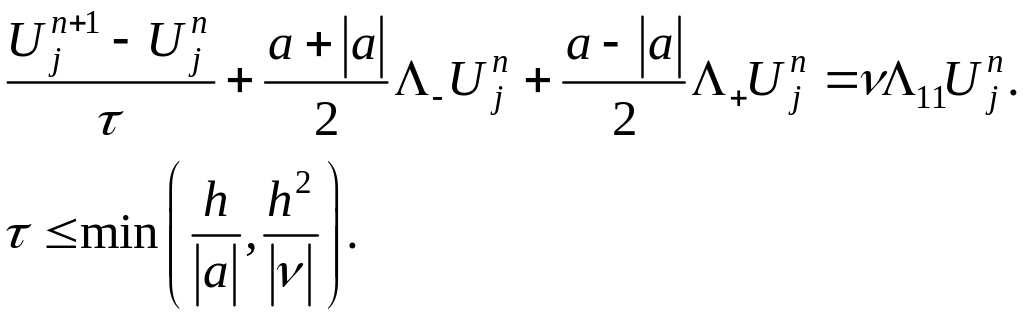 (2.1)
(2.1)
Запишем схемы Лакса-Вендрофа и Маккормака (схемы второго порядка аппроксимации). Это схемы типа «предиктор-корректор»
Схема Лакса-Вендрофа:

![]() .
.
Если
![]() ,
то получим схему со вторым порядком
аппроксимации. Неудобство этой схемы
– дробный шаг по времени.
,
то получим схему со вторым порядком
аппроксимации. Неудобство этой схемы
– дробный шаг по времени.
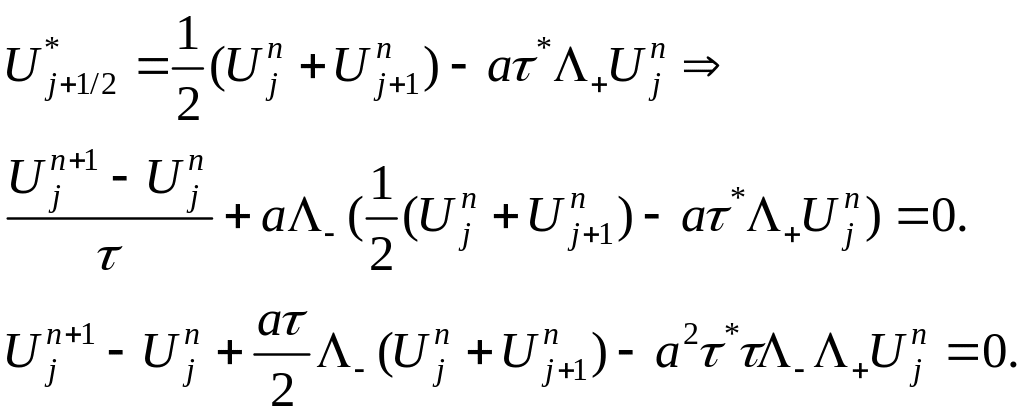
Разложим функции в ряд Тейлора
Пусть , то получим:
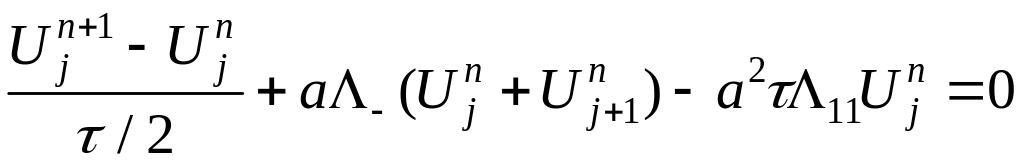 .
.
Имеем
![]() .
.
Схема Лакса-Вендрофа условно устойчива. Условие устойчивости совпадает с условием устойчивости схем (1) и (2):
.
Схема Маккормака для нелинейного уравнения (3):
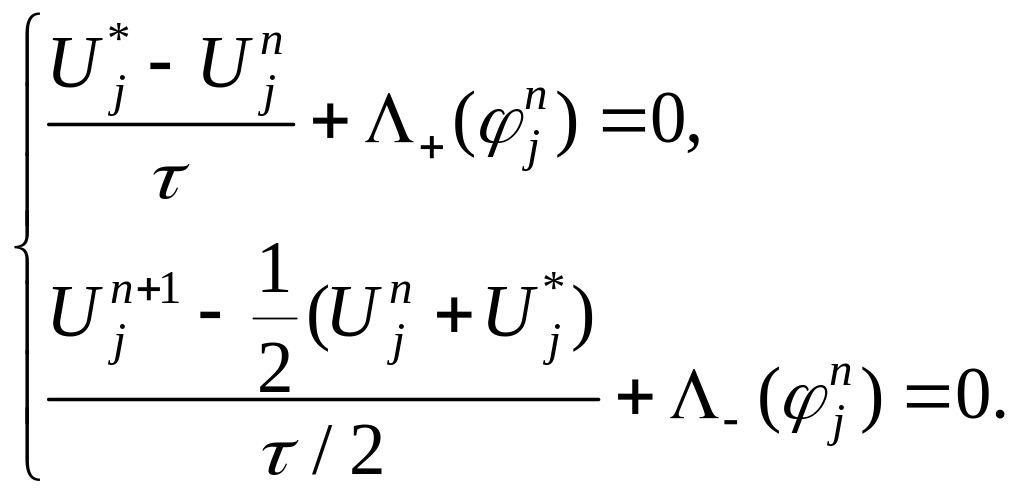
Порядок
аппроксимации:
![]() и схема условно устойчива.
и схема условно устойчива.
1.4.3. Безусловно устойчивые разностные схемы
Замечания. Схема Маккормака в целых шагах совпадает со схемой Лакса-Вендрофа. Поэтому условия аппроксимации у нее такие же, как и у схемы Лакса-Вендрофа.
Явные схемы налагают ограничения на временной шаг, что становится неэкономичным.
Поэтому более экономичные – безусловно устойчивые разностные схемы.
Схема бегущего счета ( промежуточная схема )
Рассмотрим уравнение (1)
![]() и
для него построим схему (1)
и
для него построим схему (1)
Шаблон используемый в схеме следующий:
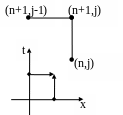
Выражая значения на верхнем временном слое имеем
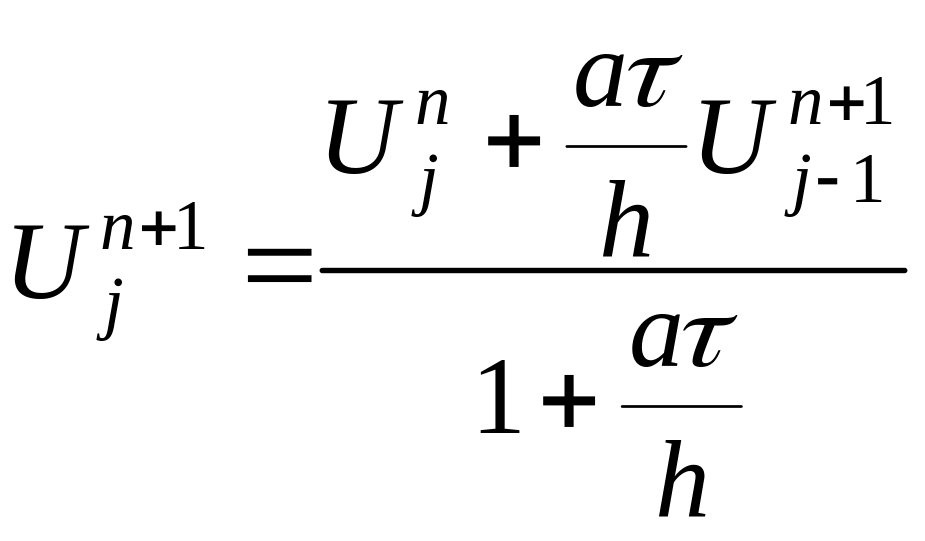 .
.
Данная
схема будет безусловно устойчивой, так
как изначально она неявная. По
арифметическим затратам она эквивалентна
явной схеме. Недостаток:
![]() .
Если это условие не выполняется, то
расчет усложняется.
.
Если это условие не выполняется, то
расчет усложняется.
