1.3.5. Упрощенные модели систем уравнений Навье-Стокса. Теория пограничного слоя
Рассматривается течение при больших числах Рейнольдса. Течение вязкой теплопроводной жидкости.
Рассмотрим ламинарный пограничный слой на примере плоской пластины. Область, близкая к пластине, называется пограничным слоем.
–
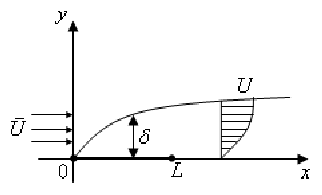
толщина
пограничного слоя, L
– длина пластины.
Малые слагаемые в уравнении выбрасываются.
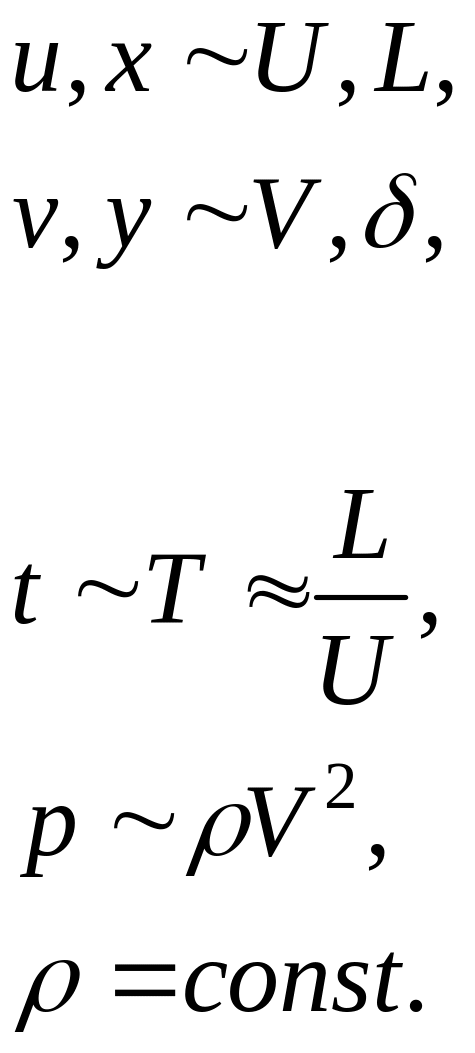
Уравнение неразрывности:
.
.
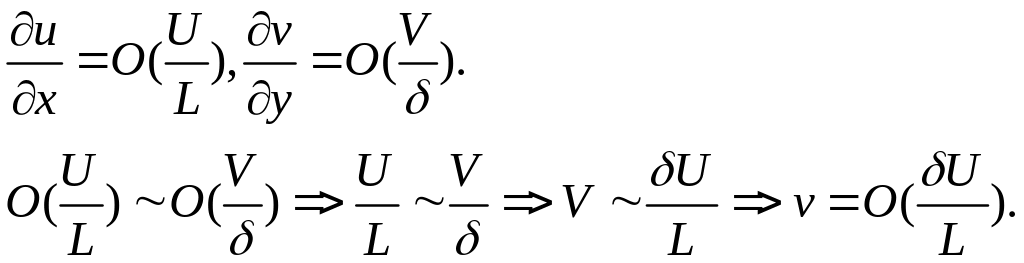
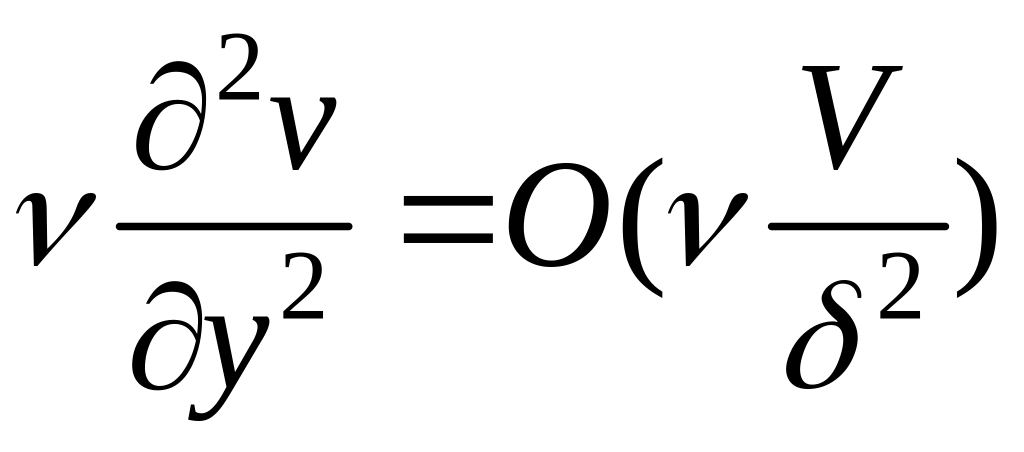При исследовании пограничного слоя влияние вязких слагаемых сопоставимо с влиянием конвективных слагаемых, связанных с силами давления на течения жидкости. То есть по порядку эти слагаемые должны быть одинаковы. Отсюда получим условие на δ:
Выбирая δ, получим:
.
.
Остается
только слагаемое
и
.
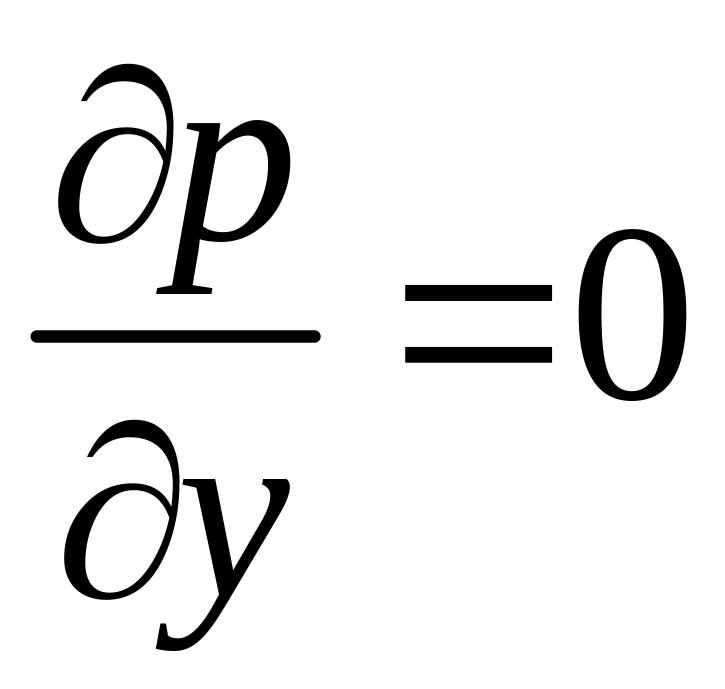Получим систему пограничного слоя.
Эта система была предложена Прандтлем и используется только для расчета течения в пограничном слое. Ее нельзя использовать для внешнего течения. Но если 2-е уравнение заменить на
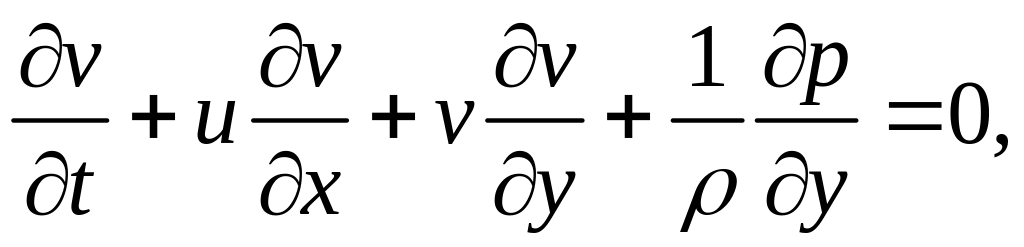
то получаем систему уравнений вязкого ударного слоя, которое уже может быть использовано для внешнего течения.
1.3.6. Параболизированная система уравнений Навье-Стокса
ПУНС используется при численном исследовании сверхзвуковых течений (особенно стационарных задач) и получается из полной системы после исключения всех 2-х производных (повторных и смешанных), содержащих дифференцирование переменной вдоль потока.
ПУНС занимает промежуточное место между полной системой уравнений Навье-Стокса и обобщенными уравнениями Прандтля, так как содержит слагаемого старшего порядка малости, чем в уравнении пограничного слоя.
Рассмотрим задачу обтекания плоской пластины, поставленной по направлению потока в плоскости XoZ.
Выпишем полную систему уравнений Навье-Стокса. Рассмотрим стационарный случай.
.
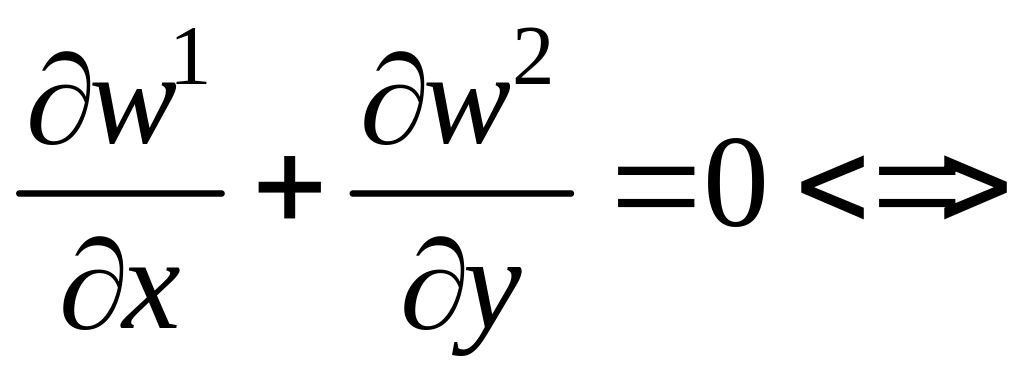
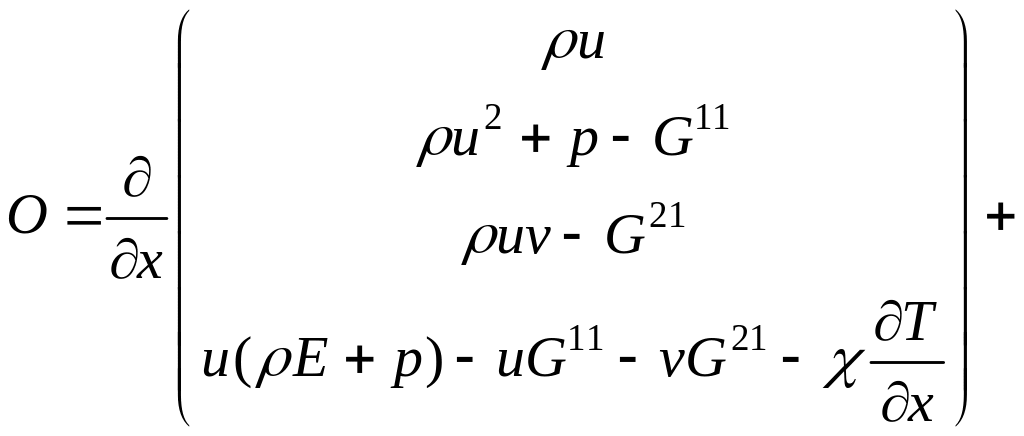
Оценим малость вязких слагаемых полной системы уравнений.
.
Была
введена малая величина
.
Тогда:
,
где
– число Прандтля.
Пораболизированная
система уравнений Навье-Стокса получается
при выбрасывании всех повторных
производных, содержащих хотя бы одно
дифференцирование по
.
Система уравнений Прандтля, полученная ранее, представляет собой первое «приближение», точнее приближение, содержащее малый параметр в нулевой степени в асимптотическом разложении решений уравнений Навье-Стокса по малому параметру.
При
последующих приближениях, содержащих
и
,
получают систему обобщенных уравнений
Прандтля. Для получения этой системы
используют уже криволинейную систему
координат, учитывая кривизну тела.
Выпишем обобщенную систему уравнений Прандтля в системе координат, связанной с телом (естественная система координат).
Рассмотрим обтекание конечного тела следующей конфигурации.
– длина
дуги контура тела, отсчитанной от
критической точки О.
–
внешняя
нормаль.
– расстояние
до оси тела.
В
уравнении Навье-Стокса содержатся члены
порядка
и
.
–
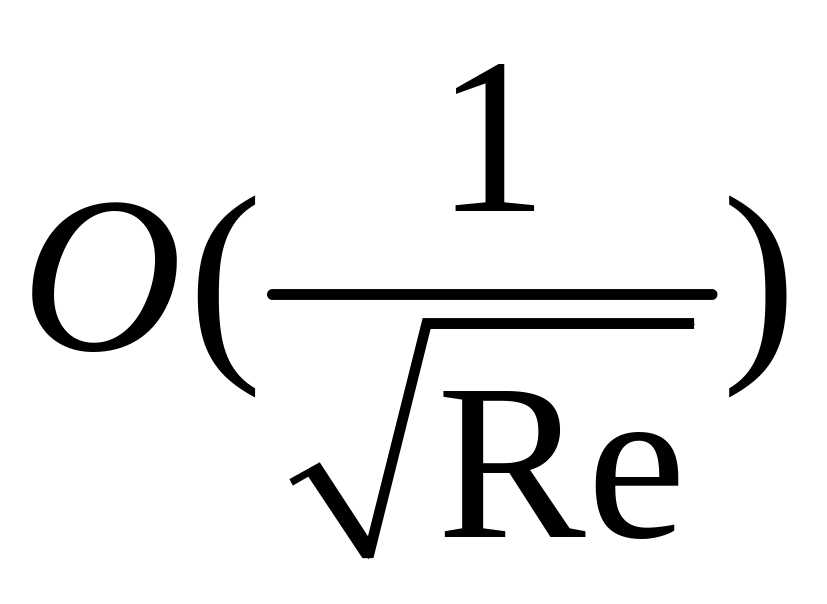коэффициенты
Ламе
Система уравнений Прандтля
1.3.7. Иллюстрация применимости моделей
Рассмотрим задачу обтекания конечного тела потоком сжимаемого вязкого теплопроводного газа.
Решение задачи может быть получено при умеренных числах Маха (не больше 6), так как при М≈6 температура газа у поверхности тела может достигать нескольких тысяч градусов. А в такой ситуации для правильного описания течения необходимо рассматривать течение, как многокомпонентную химически реагирующую смесь.
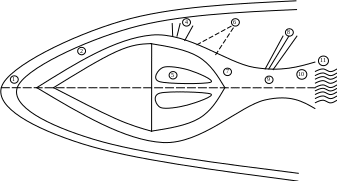
1 – Головной скачок уплотнения.
2 – Область слабовязкого течения между ударной волной и пограничным слоем.
3 – Пограничный слой.
4 – Волны разрежения.
5 – Область возвратного течения.
6 – Кормовой скачок.
7 – Весящий пограничный слой.
8 – Хвостовой скачок.
9 – Горло следа.
10 – Ближний след.
11 – Дальний след.
В области 2 справедлива модель газовой динамики, в 3 – уравнение Прандтля, в 5 и 9 уравнение Навье-Стокса (полная система), в 10 и 11 – упрощенные модели.
При
малых
область 3 стягивается.