Умови кутового розв’язку:

1. , коли .

2. , коли .

Приклад 3.1. Функція корисності споживача є випукла вгору² і задається рівнянням , ціни товарів та відповідно дорівнюють грн., грн., а дохід споживача на придбання цих двох товарів становить грн. Визначити рівноважний набір споживача і його максимальну корисність.

Розв’язання.

Рис. 3.3. Кутовий розв’язок при випуклих вгору уподобаннях споживача.

Оскільки функція корисності є випуклою вгору (рис. 3.3), то рівновагою буде кутовий розв’язок, за якого досягається максимальна корисність. Визначимо максимальний обсяг кожного з товару, який може придбати споживач при даному доході. , , одиниць; , , одиниць. ютилів, ютилів. Тож ютилів, а рівноважний набір .

Приклад 3.2. Функція корисності споживача є випукла вниз³ і задається квазілінійним рівнянням , ціни товарів та відповідно дорівнюють грн., грн., а дохід споживача на придбання цих двох товарів становить грн. Визначити рівноважний набір споживача і його максимальну корисність.

Розв’язання.

Бюджетне обмеження споживача задається рівнянням . Граничні корисності та відповідно дорівнюють , . За умовою максимізації одержимо: або , звідси , тому .

Якщо ціна товару зменшиться до , то з умови максимізації одержимо , звідси , що неможливо. Тож маємо кутовий розв’язок , .

3.3. Аналітична інтерпретація максимізації корисності

Випадок для товарів. Функція корисності , бюджетне обмеження або , де , - обсяг споживання -го товару споживачем, - ціна -го товару, - дохід споживача.

Складемо функцію Лагранжа:

.

Знайдемо часткові похідні для функції Лагранжа і прирівняємо їх до нуля, одержимо рівняння:

.

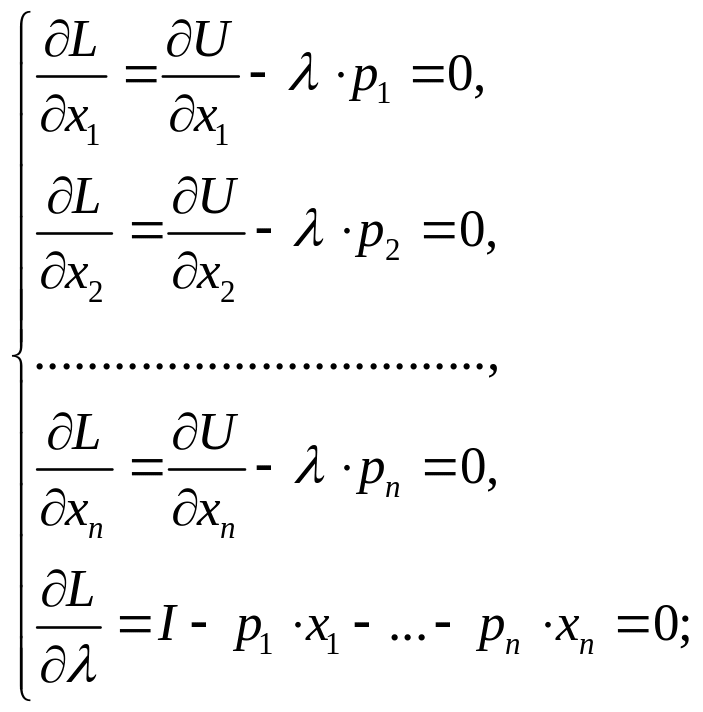
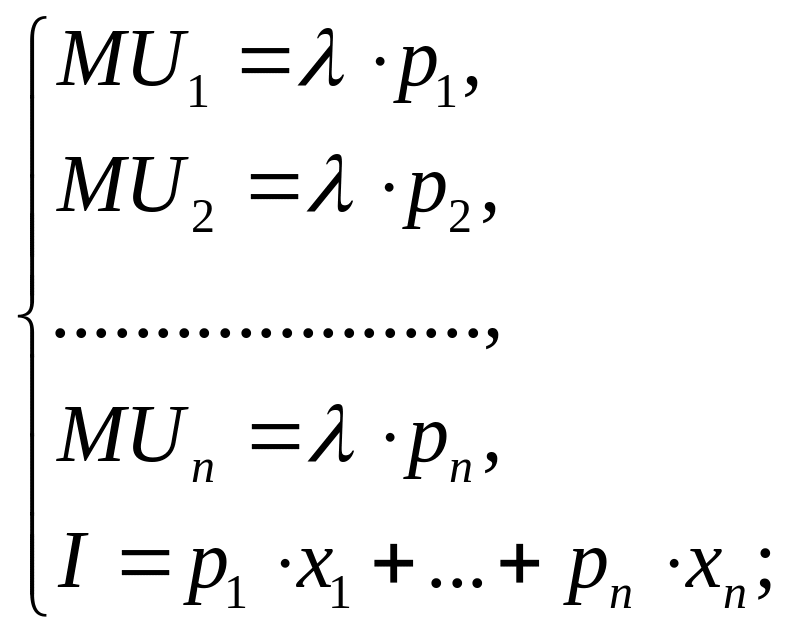
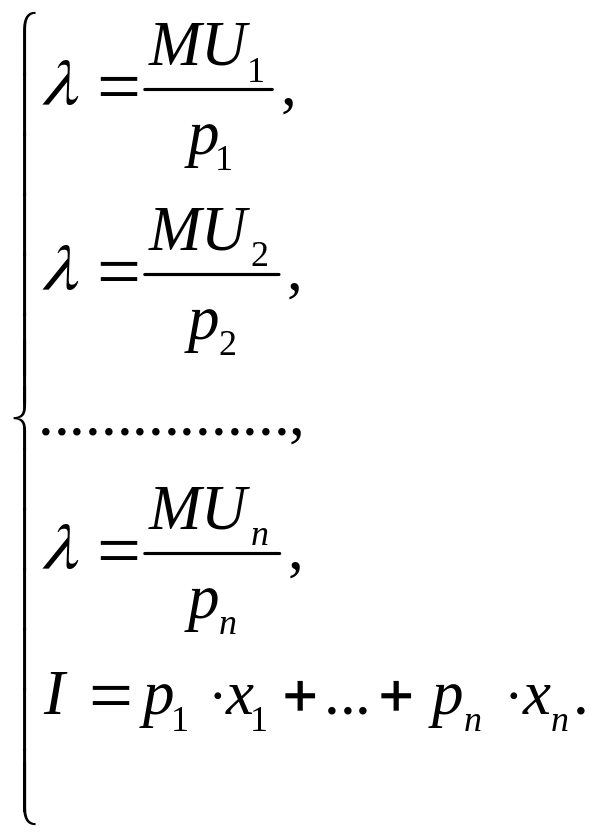Розв’язок

- умова максимізації корисності споживача для товарів, де - гранична корисність від додаткової гривні, витраченої на споживання.

Висновок: у точці максимізації корисності придбаний товар має приносити однакову граничну корисність на кожну останню витрачену на товар гривню. Якщо ця умова не виконуватиметься, це означає, що певний товар може принести більше граничної корисності на 1 грн., а тому дохід розподілений неоптимально.

Випадок для 2 товарів. Функція корисності , бюджетне обмеження або .

Метод 1. Складемо функцію Лагранжа:

.

Визначимо часткові похідні функції Лагранжа, матимемо:

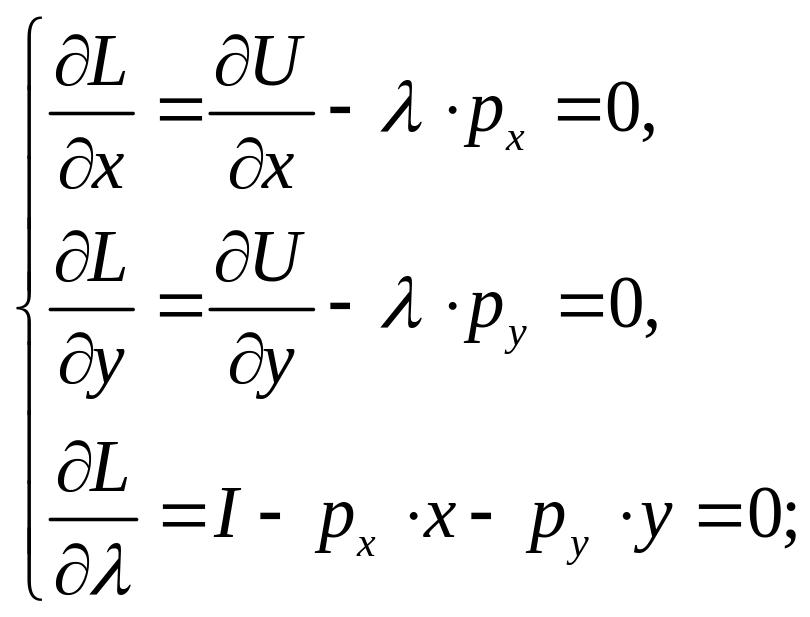
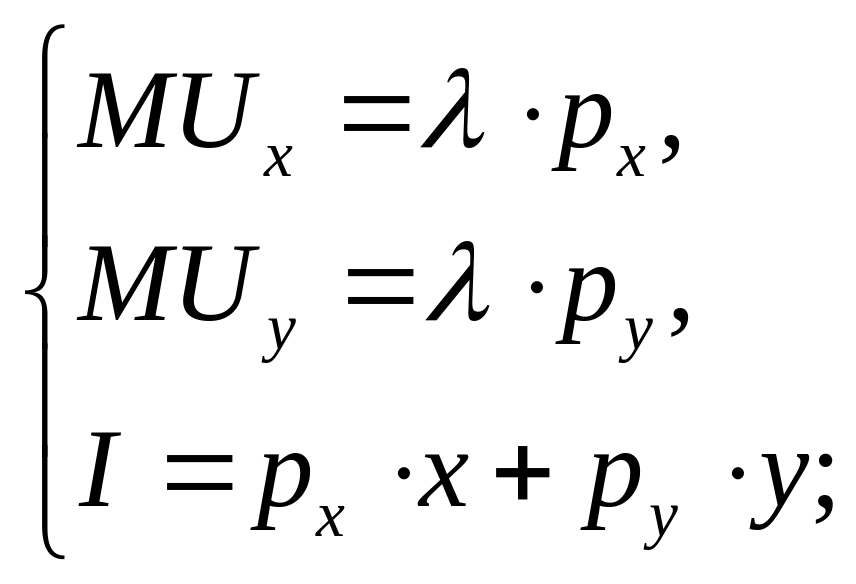
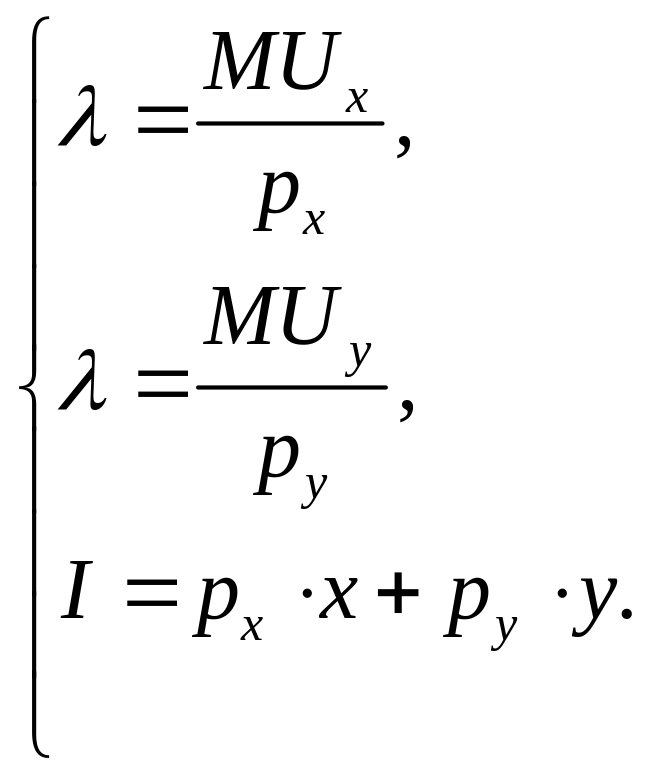
Звідси одержимо: - умова максимізації корисності споживача для 2-х товарів при даному бюджетному обмеженні.

Метод 2. Перепишемо бюджетне обмеження у вигляді: і підставимо його у функцію корисності , одержимо: .

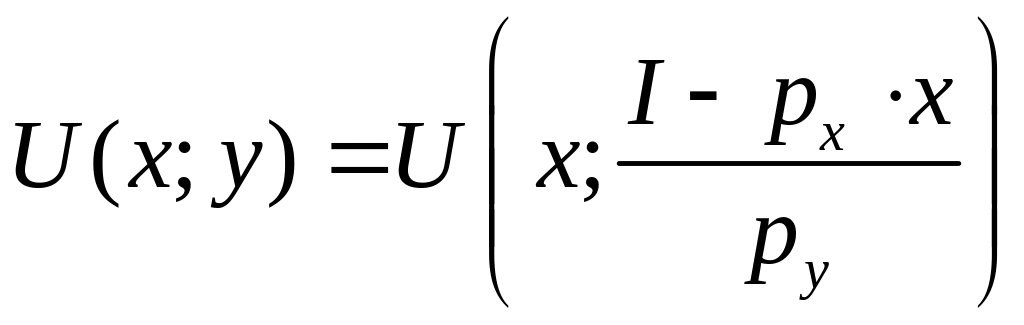Необхідна умова максимуму функції корисності визначатиметься наступним виразом:

, звідки 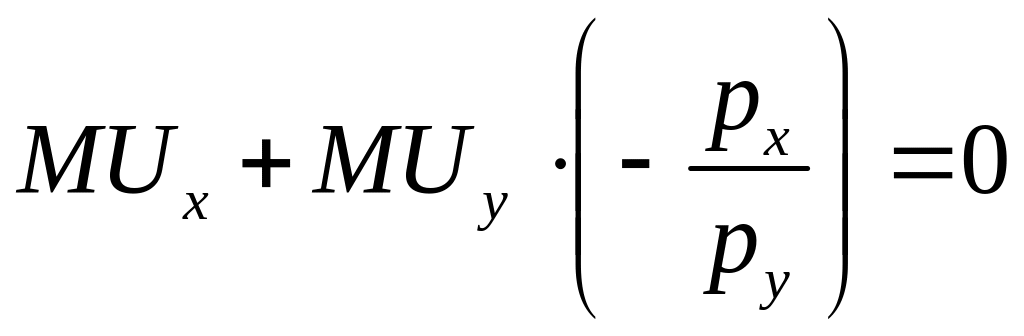, тож отримаємо .

Приклад 3.3. Знайти оптимальні обсяги споживання , для функції корисності Коба–Дугласа , де при бюджетному обмеженні за допомогою методу Лагранжа.

Розв’язання. Побудуємо функцію Лагранжа . Знайдемо всі її часткові похідні, одержимо:

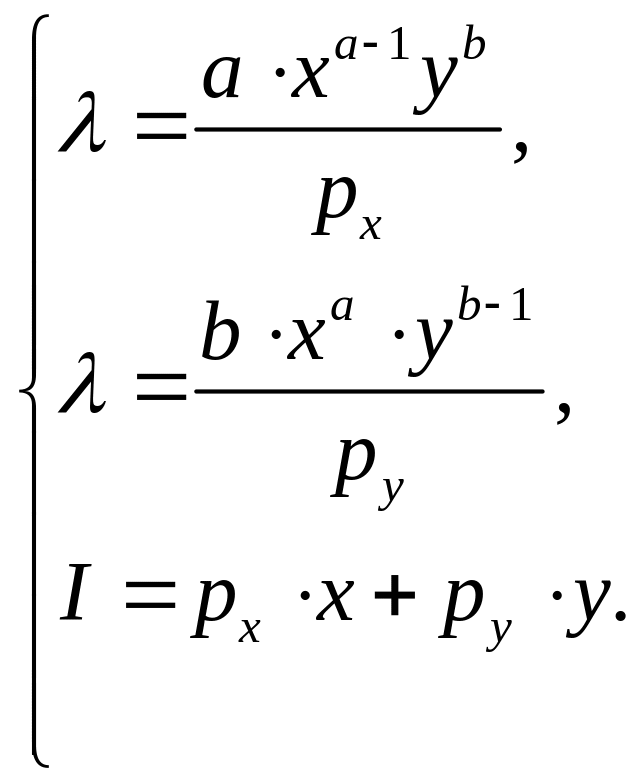
Прирівняємо праві частини перших двох рівнянь останньої системи, отримаємо:

, звідси або .

Підставимо одержане значення в третє рівняння останньої системи, матимемо: . З останнього виразу визначимо оптимальний обсяг попиту на товар і аналогічно - на товар :

, . (3.1)

Тож параметри і обчислюються як , .

Висновок: індивід за даних уподобань витрачатиме % свого доходу на товар і % - на товар .

Приклад 3.4. грн., грн., грн., .

За формулами (3.1) одержимо: одиниці, . Корисність, одержана індивідом від придбання даного набору, становитиме ютилі.

Визначимо множник Лагранжа . Він показує, що зміна в доході на 1% підвищуватиме корисність на 0,25%.