
- •Лекція 14: інтегральне числення: невизначений інтеграл
- •12.1. Первісна функція та невизначений інтеграл. Основні поняття
- •12.2.Властивості невизначеного інтеграла (правила інтегрування)
- •1. Похідна від невизначеного інтеграла існує в кожній точці [a,b], за винятком, можливо, зліченої множини точок. При цьому у точках диференційовності вона дорівнює підінтегральній функції
- •12.3.Таблиця основних інтегралів
- •12.4.Метод заміни змінної
- •12.5.Інтегрування частинами
- •12.6.Інтегрування раціональних дробів
- •12.7.Інтегрування деяких видів ірраціональних функцій
- •5. Інтеграли виду , де Рп (х) – многочлен п-го ступеня.
- •12.8. Інтеграли від диференціальних біномів , де m, n, p - раціональні числа.
- •12.9.Інтегрування тригонометричних функцій
- •6. Інтеграли виду .
- •12.10. Тригонометричні підстановки.
6. Інтеграли виду .
Тригонометричні формули
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
![]() (3)
(3)
дають можливість добуток тригонометричних функцій представити у вигляді суми.
Приклади 20. Знайти інтеграли
1)
![]() .
.
Використовуючи формулу (1), одержимо
![]()
![]() .
.
2)![]() .
.
Застосуємо
до добутку
![]() формулу (2):
формулу (2):
![]()
![]() .
.
Знову використовуючи ту ж формулу, знаходимо
![]()
![]() .
.
12.10. Тригонометричні підстановки.
Інтеграли
виду
![]() ,
,![]() приводяться до інтегралів від раціональної
відносно
приводяться до інтегралів від раціональної
відносно
![]() й
й
![]() функції за допомогою належної
тригонометричної підстановки: для
першого інтеграла
функції за допомогою належної
тригонометричної підстановки: для
першого інтеграла
![]() (або
(або
![]() ),
для другого
),
для другого
![]() (або
(або
![]() )
і для третього
)
і для третього
![]() (або
(або
![]() ).
).
Приклади 21. Знайти інтеграли
1)
![]() .
.
Покладемо
,
тоді
![]() і заданий інтеграл матиме вигляд
і заданий інтеграл матиме вигляд
![]()
![]()
![]() .
.
Для
знаходження інтегралу
![]() ми
скористалися формулою
ми
скористалися формулою
![]() ,
тому що з її допомогою легше перейти до
минулої змінної х.
Таким
чином, одержуємо
,
тому що з її допомогою легше перейти до
минулої змінної х.
Таким
чином, одержуємо
![]() ,
,
де
![]() .
Отже,
.
Отже,
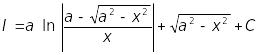 .
.
2)
![]() .
.
Застосуємо
підстановку
,
звідки
![]() .
Тоді одержимо
.
Тоді одержимо
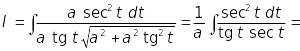
![]() ,
,
де
![]() й, отже,
й, отже,
![]() .
.
Отже,
 .
.
