12.7.Інтегрування деяких видів ірраціональних функцій

1. Інтеграли виду де R – раціональна функція; m₁, n₁, m₂, n₂, … - цілі числа. За допомогою підстановки де s – найменше спільне кратне чисел n₁, n₂,…, вказаний інтеграл перетвориться на інтеграл від раціональної функції.

Приклад 7. Знайти інтеграл

Тут тому Застосуємо підстановку тоді і, отже,

Повернемося до минулої змінної. Якщо тоді

2. Інтеграли виду Такі інтеграли шляхом виділення повного квадрата із квадратного тричлена зводиться до табличних інтегралів 20 або 21.

Приклади 8. Знайти інтеграли

1) .

Перетворимо квадратний тричлен до виду . Тоді

.

2)

.

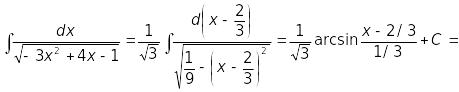
3. Інтеграли виду . Для знаходження цього інтеграла виділимо в чисельнику похідну квадратного тричлена, що стоїть під знаком кореня, і розкладемо інтеграл на суму двох інтегралів:

.

Перший з отриманих інтегралів є табличним інтегралом 17, а другий розглянутий у п. 2.

Приклади 9. Знайти інтеграл

1) .

Виділимо в чисельнику похідну підкореневого виразу:

.

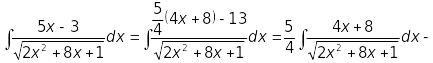
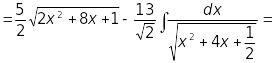
2) .

.

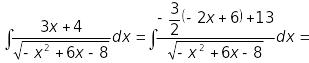
4. Інтеграли виду . За допомогою підстановки цей інтеграл приводиться до розглянутого в п. 2.

Приклади 10. Знайти інтеграли

1) .

Покладемо , тоді та

.

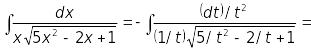
2) .

Покладемо , тоді та . Отже,

.

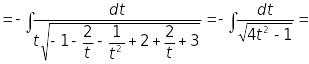
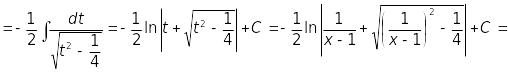
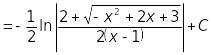3) .

Записавши чисельник підінтегральної функції у вигляді , одержимо

.

Представимо даний інтеграл як різницю з двох інтегралів:

.

До першого інтегралу застосуємо формулу 21, а до другого – підстановку :

.

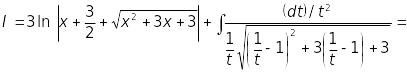
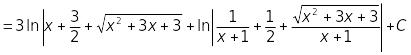5. Інтеграли виду , де Рп (х) – многочлен п-го ступеня.

Інтеграл такого виду знаходиться за допомогою тотожності

,

де багаточлен -го ступеня з невизначеними коефіцієнтами, λ - число.

Диференціюючи зазначену тотожність приведемо результат до загального знаменника, тоді одержимо рівність двох багаточленів, з якої можна визначити коефіцієнти багаточлена та число λ.

Приклади 11. Знайти інтеграли

1) .

Тут п=3, тоді відповідна тотожність має вигляд

.

Диференціюючи обидві його частини, одержуємо

.

Звільняємося від знаменника:

,

або

.

Порівнюючи коефіцієнти при однакових ступенях х, одержимо

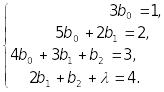
Розв’язуючи систему, знайдемо . Отже,

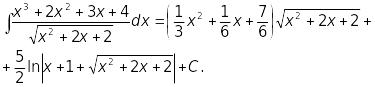
12.8. Інтеграли від диференціальних біномів , де m, n, p - раціональні числа.

Як довів П. Л. Чебишев, інтеграли від диференціальних біномів виражаються через елементарні функції тільки в трьох випадках:

1) р – ціле число, тоді даний інтеграл зводиться до інтегралу від раціональної функції за допомогою підстановки , де s – найменше загальне кратне знаменників дробів m та n;

2) - ціле число, у цьому випадку даний інтеграл раціоналізується за допомогою підстановки ;

3) - ціле число, у цьому випадку до тієї ж мети призведе підстановка , де s – знаменник дробу р.

Приклади 12. Знайти інтеграли

1) .

Підінтегральну функцію можна записати у вигляді , тобто ціле число. Виходить, маємо перший випадок інтегрування диференціального бінома. Тому варто застосовувати підстановку ; тоді та шуканий інтеграл приймає вигляд

.

Останній інтеграл знаходиться таким чином:

.

Таким чином,

.

2) .

Переписавши підінтегральну функцію у вигляді , маємо . Тому що ціле число, то має місце другий випадок інтегрування. Використовуючи підстановку , одержимо . Отже,

.

3) .

Тут і ціле число. Тому має місце третій випадок інтегрування диференціального бінома. Покладемо ; тоді . Перетворимо даний інтеграл у такий спосіб:

.

Отже,

.