12.9.Інтегрування тригонометричних функцій

1. Інтеграли виду , де R – раціональна функція. Інтеграли зазначеного виду приводяться до інтегралів від раціональних функцій за допомогою так називаної універсальної тригонометричної підстановки . У результаті цієї підстановки маємо:

.

Приклади 13. Знайти інтеграли

1) .

Підінтегральна функція раціонально залежить від й ; застосуємо підстановку , тоді та

.

Повертаючись до минулої змінної, одержимо

.

2) .

Покладемо , тоді одержимо

.

Універсальна підстановка в багатьох випадках приводить до складних обчислень, тому що при її застосуванні та виражаються через t у вигляді раціональних дробів, що містять .

У деяких випадках знаходження інтегралів виду може бути спрощено.

1. Якщо непарна функція відносно sin x, тобто якщо , то інтеграл раціоналізується підстановкою .

2. Якщо непарна функція відносно cos x, тобто якщо , тоді інтеграл раціоналізується за допомогою підстановки .

3. Якщо парна функція відносно sin x й cos x, тобто якщо , тоді доцільно застосувати підстановку .

Приклади 14. Знайти інтеграли

1) .

Оскільки підінтегральна функція непарна відносно синуса, тоді покладемо . Звідси . Таким чином,

.

Отже,

.

Відзначимо, що в розглянутому випадку інтеграл завжди може бути записаний у вигляді .

2) .

Тут підінтегральна функція є непарною відносно косинуса. Тому застосовуємо підстановку ; тоді . Отже,

.

Оскільки , то

.

Остаточно одержуємо

.

Відзначимо, що в розглянутому випадку інтеграл завжди може бути записаний у вигляді .

3) .

Підінтегральна функція парна відносно синуса та косинуса. Покладемо ; тоді ; ; . Звідси

.

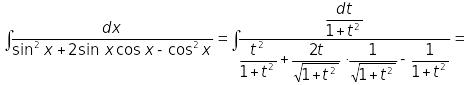
Далі, маємо

.

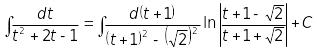і, отже,

.

Відзначимо, що знаходження інтегралу можна спростити, якщо у вихідному інтегралі розділити чисельник і знаменник на :

.

2. Інтеграли виду . Виділимо тут два випадки, що мають особливо важливе значення.

Випадок 1. Принаймні один з показників m або n – непарне додатне число.

Якщо n – непарне додатне число, то застосовується підстановка ; якщо ж m – непарне додатне число, - підстановка .

Приклади 15. Знайти інтеграли

1) .

Покладемо , тоді одержимо

.

2) .

Маємо

.

Якщо , тоді отримаємо

.

Випадок 2. Обидва показники ступеня m й n - парні додатні числа. Тут варто перетворити підінтегральну функцію за допомогою формул

(1)

(2)

(3)

Приклади 16. Знайти інтеграли

1) .

З формули (1) витікає, що

.

Застосувавши формулу (2), одержуємо

.

Отже,

.

2) .

Використовуючи формулу (3), одержимо

.

3) .

.

3. Інтеграли виду та , де m – ціле додатне число. При знаходженні таких інтегралів застосовується формула (або ), за допомогою якої послідовно знижується ступінь тангенса або котангенса.

Приклади 17. Знайти інтеграли

1) .

.

2) .

.

4. Інтеграли виду й , де п – парне додатне число. Такі інтеграли знаходяться аналогічно розглянутим у п. 3 за допомогою формули (або ).

Приклади 18. Знайти інтеграли

1) .

.

2) .

.

5. Інтеграли виду й . Інтеграли від непарного додатного ступеня секанса або косеканса простіше всього знаходяться за рекурентними формулами:

. (1)

. (2)

Приклади 19. Знайти інтеграли

1) .

Застосовуючи рекурентну формулу (2) при , тобто при , одержимо

;

покладаючи , тобто , за тією ж формулою маємо

.

Оскільки , тоді

,

.