Работа № 12 изучение работы простейшего лампового генератора электромагнитных колебаний

Приборы и принадлежности: трехэлектродная лампа, источник постоянного напряжения на 300 В, источник переменного напряжения на 4В, два воздушных конденсатора постоянной и переменной емкости, две катушки индуктивности, два конденсатора постоянной емкости, сопротивление, микроамперметр, индикатор высокочастотного электромагнитного поля на неоновой лампе, неизвестные емкость и индуктивность.

Краткая теория

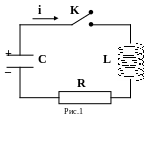
Электрический колебательный контур представляет собой цепь (рис.1), состоящую из последовательно соединенных емкости С, индуктивности L и сопротивления R проводников.

В контуре происходят периодические изменения силы тока и связанных с ней величин. Перезарядку пластин конденсатора можно понять, вспомнив, в чем состоит явление самоиндукции.

Явление самоиндукции состоит в следующем: при всяком изменении тока в контуре в нем возникает э.д.с. самоиндукции _c, которая прямо пропорциональна скорости изменения тока в контуре (di/dt) и обратно этой скорости направлена:

ε . (1)

Если ток нарастает, э.д.с. препятствует этому увеличению тока и создает индукционный ток противоположного направления. Если ток уменьшается, э.д.с. препятствует уменьшению тока и создает индукционный ток того же направления.

Рассмотрим работу контура. Зарядим конденсатор от внешнего источника электроэнергии до некоторой разности потенциалов U, сообщив его обкладкам заряды q, и затем с помощью ключа К замкнуть контур, то конденсатор начнет разряжаться и в цепи потечет некоторый ток. При малом значении R он будет очень быстро нарастать. Направление для тока i, показанное на рис.1, примем за положительное (верхняя пластина заряжена положительно, нижняя - отрицательно) и рассмотрим процессы, протекающие в контуре. Допустим сначала, что омическое сопротивление проводника, из которых состоит контур, мало, т.е. R0, и пусть в начальный момент времени заряд конденсатора максимален (q=q_o). При этом разность потенциалов между его обкладками также максимальна (U=U_o), а ток в цепи равен нулю (рис.2,а).

Когда конденсатор начнет разряжаться, то в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность.

Так как в цепи действует э.д.с. самоиндукции, ток будет увеличиваться постепенно, и через время t=1/4 T (четверть периода) он достигнет максимального значения (i=i_o), конденсатор разрядится полностью, и электрическое поле исчезнет, т.е. q=0 и U=0. Теперь вся энергия контура сосредоточена в магнитном поле катушки (рис.2,б). В последующий момент времени магнитное поле катушки начнет ослабевать, в связи с чем в ней индуцируется ток, идущий (согласно правилу Ленца) в том же направлении, в котором шел ток разрядки конденсатора. Благодаря этому конденсатор перезаряжается. Через время t=1/2 T магнитное поле исчезнет, а электрическое поле достигнет максимума. При этом q=q_o, U=U_o и i=0. Таким образом, энергия магнитного поля катушки индуктивности превратится в энергию электрического поля конденсатора (рис.2,в). Через время t=3/4 T конденсатор полностью разрядится, ток опять достигнет максимальной величины (i=i_o), а энергия контура сосредоточится в магнитном поле катушки (рис.2,г). В последующий момент времени магнитное поле катушки начнет ослабевать и индукционный ток, препятствующий этому ослаблению, перезарядит конденсатор. В результате к моменту времени t=T система (контур) возвращается в исходное состояние (рис.2,а) и начинается повторение рассмотренного процесса.

В ходе процесса периодически изменяются (колеблются) заряд и напряжение на конденсаторе, сила и направление тока, текущего через индуктивность. Эти колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.

Таким образом, если сопротивление контура равно нулю, то указанный процесс будет продолжаться неограниченно долго и мы получим незатухающие электрические колебания, период которых будет зависеть от величин L и С (см.ниже формулу Томсона).

Колебания, происходящие в таком идеальном контуре (R=0), называются свободными, или собственными, колебаниями контура.

Выведем теперь уравнение, описывающее колебательный процесс в контуре. Для этого будем считать, что электрические процессы в контуре квазистационарны. Это значит, что мгновенное значение силы тока одно и то же в любом месте контура. При этих условиях можно использовать второе правило Кирхгофа для постоянного тока: в замкнутом контуре разветвленной цепи алгебраическая сумма э.д.с. источников тока равна алгебраической сумме произведений сил тока на сопротивления соответствующих участков этого контура.

Тогда, выбрав направление обхода контура, показанное на рис.1 стрелкой, в качестве положительного получим

U + _c = iR, (2)

где - напряжение на пластинах конденсатора, ε_С - э.д.с. самоиндукции катушки индуктивности. Или . (3)

Ток является разрядным током конденсатора и в данном случае показывает, на какую величину уменьшается заряд конденсатора в единицу времени. Так что с учетом знака в явном виде имеем:

(4)

Подставив (4) в (3), получим (5)

Итак, закон изменения величины заряда конденсатора к колебательном контуре удовлетворяет дифференциальному уравнению второго порядка. Для идеального колебательного контура, когда R=0, уравнение (5) принимает вид (6)

Это уравнение при постоянных L и С аналогично связи между ускорением колеблющегося тела и смещением х от положения равновесия при гармоническом колебательном движении: (7)

Решая дифференциальное уравнение (6), получим следующий закон изменения зарядов на пластинах конденсатора: (8)

где q₀ - максимальное значение заряда, которое определяется из начальных условий, - собственная (круговая) частота электрических колебаний. С учетом связи между круговой частотой и периодом колебаний имеем: . (9)

Откуда . (10)

Данное уравнение (10) называется формулой Томсона.

В реальном колебательном контуре омическое сопротивление R нельзя свести к нулю. Поэтому в нем электрические колебания всегда будут затухающими, так как часть энергии будет затрачиваться на нагревание проводников (Джоулево тепло).

Для осуществления незатухающих электрических колебаний необходимо обеспечить автоматическую подачу энергии с частотой, равной частоте собственных колебаний контура, т.е. необходимо создать автоколебательную систему. Такой системой незатухающих колебаний является ламповый генератор.