Упражнение 3 Проверка обобщенного закона Ома

С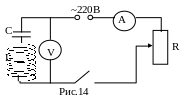 обрать схему согласно рис.14. Установив реостат на максимальное сопротивление, замкнуть ключ. Изменяя сопротивление реостата, установить по амперметру те же значения сил переменных токов, что и в упражнении 1, и для этих значений токов по вольтметру, зафиксировать соответствующие значения напряжений. Данные занести в таблицу.

Измерив по приборам значения i_эфф и U_эфф, определить по формуле полные сопротивления цепи для разных значений тока и напряжения.

№ п//п	Uэфф,В	iэфф,А	Z,Ом	Z выч,Ом	0
1
2
3

По формуле (14) подстановкой в нее ранее найденных значений R, L и C вычислить полное сопротивление Z _выч. Совпадение значений Z , определенных в данном упражнении, и Z _выч и является проверкой обобщенного закон Ома для цепи переменного тока с учетом погрешностей эксперимента. Данные занести в табл.3. Следует отметить, что сопротивление катушки индуктивности переменному току при наличии железного сердечника в ней зависит от силы тока, поэтому сравнивать измеренные и вычисленные значения можно только для одних и тех же значений силы тока.

По формуле (17) рассчитать угол сдвига фаз  между током и напряжением по ранее найденным значениям R, L и C.

Работа № 10 измерение удельного сопротивления проводника

Приборы и принадлежности: установка для измерения сопротивления, микрометр.

Краткая теория

Высокая электрическая проводимость металлов обусловлена огромной концентрацией в них носителей тока – электронов проводимости. В классической электронной теории Друде-Лоренца электроны проводимости рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа. Концентрация электронов проводимости n в одновалентном металле имеет порядок числа атомов в единице объема металла:

n ≈ ( 10²⁸ - 10²⁹)м^-3.

В отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются с ионами металла, которые в свою очередь совершают беспорядочные тепловые колебания около положений равновесия – узлов кристаллической решетки. В данной теории считается, что средняя длина свободного пробега электронов приблизительно равна расстоянию между узлами решетки металла, т.е. ~10^-10 м.

Исходя из основных положений молекулярно-кинетической теории вещества, можно записать выражение для средней кинетической энергии теплового движения электронов:

(1)

где m – масса электрона, V_кв – средняя квадратичная скорость электронов, k – постоянная Больцмана, Т – термодинамическая температура.

При Т = 273 К V_кв ≈ 10⁵ м/с. Средняя арифметическая скорость теплового движения имеет значение такого же порядка.

Электрический ток в металле возникает под действием электрического поля, которое вызывает упорядоченное движения электронов проводимости – их дрейф в направлении, противоположном направлению вектора напряженности поля

Тогда плотность тока j будет равна , (2)

где е – заряд электрона, - средняя скорость дрейфа, имеющая величину порядка 10^-3 м/с.

На основании 2-го закона Ньютона F=ma можно записать

(3)

Величина еЕ в этом уравнении есть сила, действующая на электрон в электрическом поле.

В классической теории полагают, что при соударениях с ионами электроны полностью теряют скорость упорядоченного движения . Тогда , где - среднее время свободного пробега электрона, а – ускорение движения электронов.

Из уравнения (3) следует, что . Тогда средняя скорость дрейфа электронов будет равна (4)

Учитывая, что , можно записать . Подставив это выражение в формулу (4), получим

Тогда формулу (2) можно записать так: (5)

Величина называется удельной электрической проводимостью, а обратная ей величина - удельным электрическим сопротивлением проводника.

Тогда (6)

Это есть закон Ома в дифференциальной форме. Из (6) можно получить выражение для закона Ома на участке проводника длиной ℓ и сечением S.

Так как плотность тока j и сила тока J связаны соотношением а где U - разность потенциалов на концах проводника, то . Но сопротивление проводника Отсюда .

Несмотря на очевидные достоинства классической электронной теории проводимости металлов, она не смогла объяснить ряд экспериментальных фактов. Например, из эксперимента следует, что для металлов ρ ~ Т, а из теории следует, что Эти несоответствия обусловлены, во-первых, тем, что она исходит из представления об электроне как о частице, поведение которой описывается только законами классической механики, не учитывая его волновых свойств. Во-вторых, эта теория не учитывает взаимодействия электронов (в электронном газе) друг с другом. В-третьих, эта теория не учитывает, что энергия электрона в металле, как и его энергия в изолированном атоме, может принимать не любые, а только определенные (дискретные) значения.

Отмеченные особенности поведения электронов учтены квантовой электронной теорией проводимости, успешно разрешившей противоречия классической теории.