
ПЕРВЫЕ ВОПРОСЫ
ВОПРОС 1 Вывестии дифференциальное уравнение конвективной диффузии. Рассмотреть частный случай диффузии в неподвижной среде.
Рассмотрим перенос массы в неразрывном потоке жидкости при условии постоянства коэффициента молекулярной диффузии D переносимого вещества и отсутствии источников массы (т. е. γ= 0).
Плотность потока массы описывается линейным градиентным̅ уравнением (3.14) первым законом Фика.
мС= -DgradC (3.14)
В соответствии с основным уравнением переноса количества движения, энергии и массы при учете того, что
потенциалом переноса в данном случае является концентрация, получим уравнение переноса массы |
|
дс/дτ + div wc = D div grad с. |
(3.43) |
Проводя преобразования, аналогичные сделанным при выводе уравнения конвективного теплообмена, запишем это
уравнение в следующем виде: |
|
|
дс/дτ + cdiv w + wgrad с = D 2c. |
(3-44) |
|
Поскольку поток неразрывен, div w = 0. Тогда уравнение переноса массы примет вид |
|
|
дс/дτ + wgrad с = D 2c, |
(3.45) |
|
или в развернутой форме: |
|
|
дс/дt + wxdc/dx + wydc/dy + w2dc/dz = D(д2c/dx2 + д2с/8у2 + д2c/дz2) = D 2c. |
(3.46) |
|
Уравнение (3.46) выражает в общем виде распределение концентрации компонента в движущемся потоке при неустановившемся процессе переноса массы. Уравнение (3.46) называют также дифференциальным уравнением
конвективной диффузии.
Для установившегося процесса переноса массы дс/dτ = 0; тогда |
|
wxдc/дx + wyдc/дy + wzдc/дz = D 2c. |
(3.47) |
Коэффициент молекулярной диффузии D представляет собой физическую константу и характеризует способность данного вещества проникать вследствие диффузии в неподвижную среду. Он зависит от природы диффундирующего вещества и среды, температуры и давления и не зависит от гидродинамических условий, в которых происходит процесс. Отметим, что коэффициент диффузии является аналогом коэффициента температуропроводности а. Таким образом, уравнение (3.46) по структуре аналогично дифференциальному уравнению переноса теплоты (3.40).
В неподвижной среде wx = wy = wz = 0, и уравнение (3.46) обращается в дифференциальное уравнение молекулярной диффузии
дс/дτ = D(д2 с/дх1 + д2с/ду2 + д2с/дг2), |
(3.48) |
которое носит название второго закона Фика и описывает распределение концентраций данного вещества в неподвижной среде.
2. Первый закон Фика. Вывод дифференциального уравнения конвективной диффузии.
Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае происходит перенос молекул распределяемого компонента из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество вещества, продиффундировавшего в пределах фазы, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени
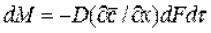 – коэффициент пропорциональности, или коэффициент диффузии.
– коэффициент пропорциональности, или коэффициент диффузии.
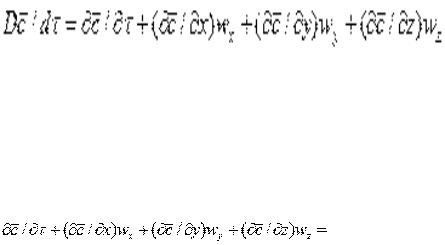
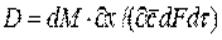 .
.
Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м2 в течение 1 с при разности концентраций на расстоянии 1 м, равной единице.
Знак минус в правой части уравнения показывает, что при молекулярной диффузии направление перемещения вещества и градиент концентраций противоположны друг другу. Размерность коэффициента зависит от способа выражения концентрации распределяемого компонента. Если это объемные концентрации, то размерность коэффициента следующая:
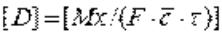 .
.
Коэффициент диффузии не является постоянной величиной. Это достаточно малая величина для газов. Она на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления. Если в газах коэффициент диффузии не зависит от концентрации диффундирующего вещества, то в жидкостях это влияние особенно значимо для неразбавленных растворов.
2)Дифференциальное уравнение массоотдачи (конвективной диффузии).
В основу рассмотрения явления конвективной диффузии положена теория диффузионного пограничного слоя. Согласно этой теории распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. При наличии конвективной диффузии концентрация распределяемого компонента изменяется не только вследствие молекулярной диффузии, но и механического переноса его из одной области пространства в другую. В этом случае концентрация распределяемого компонента будет функцией не только
координат x, y, z и времени 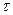 , но и составляющих скорости перемещения частиц потока
, но и составляющих скорости перемещения частиц потока 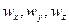 .
.
При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной точки пространства в другую:
. (4.21)
В этом равенстве 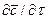 представляет собой локальное изменение концентрации распределяемого компонента, а
представляет собой локальное изменение концентрации распределяемого компонента, а
комплекс 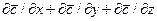 – конвективное изменение концентрации.
– конвективное изменение концентрации.
Если в уравнении молекулярной диффузии (4.17) заменить локальное изменение концентрации 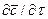 полным
полным
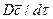 , в соответствие с уравнением (4.21), то можно получить дифференциальное уравнение конвективной диффузии:
, в соответствие с уравнением (4.21), то можно получить дифференциальное уравнение конвективной диффузии:
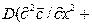
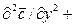
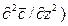 . (4.22)
. (4.22)
3. Получить диффузионные критерии подобия. Определяемый и определяющие критерии. Физический смысл массообменных критериев подобия.
Основные критерии массобменных процессов аналогичны основным критериям теплообмена.
Рассмотрим уравнения массопереноса на границе раздела фаз. Из одной фазы в другую переходит количество массы, |
||
|
гр |
гр |
равное = |
( − |
), где - равновесная концентрация на границе раздела фаз. |
Это же количество массы переносится молекулярной диффузией через пограничный слой: = − |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этих уравнениях трудноопределимы величины гр и n- толщина пограничного слоя, через который проходит вещество |
|||||||||
молекулярной диффузией. Откуда |
|
||||||||
|
|
( |
− |
|
) = − = |
|
|
|
|
|
|
гр |
|
|
|
||||
|
|
|
|
|
|
|
|
||
Перемножим на масштабные множители каждый член уравнения: |
|
||||||||
|
|
|
( ) = ( |
)(− ) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
= , откуда = ′, где l- определяющий геометрический параметр. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
Этот безразмерный комплекс является′ аналогом теплового критерия Нуссельта и называется диффузионным критерием Нуссельта (иногдаШервуда Sh). является определяемым критерием, поскольку в него входит величина . Он характеризует отношение скорости переноса вещества (конвективной и молекулярной) к молекулярному переносу.
Другие критерии получим из дифференциального уравнения конвективной диффузии, переписав его относительно оси х : |
|||||||
с |
+ ( |
с) = с |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
||||
Проведя его подобное преобразование, получаем следующие критерии подобия: |
|
= ′, где ′диффузионный |
|
||||
|
|
||||||
|
|
|
|
|
|
|
|
критерий Фурье, который характеризует подобие неустановившихся процессов массобмена; |
|
|
|||||
= ′- диффузионный критерий Пекле, характеризующий отношение переноса вещества конвекцией к |
|
|
|||||
|
|
|
|
|
|
|
|
молекулярному переносу в сходственных точках подобных систем. Часто ′ заменяют отношением: ′ = ( ) : ( ) = |
|||||||
|
|
|
|
|
|
|
|
= ′- диффузионный критерий Прандтля, он выражает постоянство отношения физических свойств жидкости или |
|||||||
|
|
|
|
|
|
|
|
газа в сходственных точках подобных систем, характеризует отношение профиля скоростей к профилю концентраций, т.е. отношение толщины гидродинамического и диффузионного пограничных слоев.
Для соблюдения подобия процессов массоотдачи необходимо также соблюдение гидродинамического подобия. Поэтому
критериальное′ = (′, уравнение, ′, ,массоотдачиГ , Г , … ) для неустановившегося процесса будет иметь вид (Г-геометрический симплекс):
При установившимся процессе и при отсутствия влияния сил тяжести ( ′ = ; = ): ′ = ( , ′, , Г , Г )
Например ′ = (′) Г Г
4. Получить уравнение аддитивности диффузионных сопротивлений. Сформулировать допущения при выводе.
Рассмотрим случай переноса вещества из фазы Фу фазу Фх; движущая сила массопередачи выражена в единицах концентрации фазы Фу. Количество вещества М, переносимое из фазы в фазу, рассчитываем из уравнения массопередачи. Допустим, что равновесная зависимость между концентрациями в фазах линейна, линия равновесия описывается уравнением у* = mx, где m – тангенс угла наклона линии равновесия.
Примем, что концентрации распределяемого вещества в фазах у границы раздела (хгр , угр) равновесны друг другу. Тогда из уравнения линии равновесия следует, что хгр = угр/m и х = у*/m, где хгр. и угр - концентрации каждой фазы, у*- концентрация фазы Фу, равновесная с концентрацией х фазы Фх.
Подставляя значения хгр. и х в уравнение массоотдачи М=βx F(xгр-x),
Получим |
М= ∙ ∙ |
− |
|
|
|
|
|
|
|
|
гр |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда |
− = |
∙ |
|
|
|
|
|
|
|
|
|
гр |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вместе с тем из уравнения массоотдачи М=βyF(y-yгр), имеем: |
|
|
|
|
|
|||||
|
|
|
− |
= |
|
|
|
|
||
|
|
|
гр |
|
∙ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Суммируем, почленно уравнения получим: |
|
|
|
|
|
|
|
|||
|
|
|
− = |
∙ ( |
1 |
+ |
) |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из уравнения массопередачи = |
∙ ∙ ( − ) находим : − = ∙ |
|
||||||||
1 |
||||||||||
Приравнивания правые части полученных выражений движущей силы (y –y*) и сокращая подобные члены, получим:
1 = 1 +
При выражении коэффициента массопередачи в концентрациях фазы Фх аналогичные рассуждения приводят к |
||||||
|
= |
|
+ |
|
|
∙ |
|
|
|
|
|||
зависимости 1 |
1 |
|
1 |
|||
5. Вывести соотношение между коэффициентами массопередачи и массоотдачи. Из каких уравнений получают коэффициенты массоотдачи?
Чтобы установить аналитическую зависимость между коэффициентами массопередачи и массоотдачи, принимают, что на границе раздела фаз достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу вещества через границу раздела фаз можно пренебречь. Отсюда как следствие вытекает положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок к расчету коэффициента массопередачи.
Допустим, что распределяемый компонент переходит из фазы G в фазу L и движущая сила выражается в концентрациях фазы G. При установившемся процессе массопередачи количество вещества, переходящее из одной фазы в другую фазу, определяется по уравнению
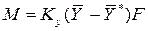 .
.
Для упрощения рассмотрим случай, когда равновесная зависимость между равновесными концентрациями представляет линейную зависимость 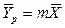 , где m – тангенс угла наклона линии равновесия.
, где m – тангенс угла наклона линии равновесия.
Из уравнения равновесия следует
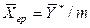 и
и 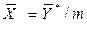 .
.
Уравнение массоотдачи для жидкой фазы
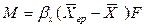 .
.
Подставляя значения 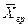 и
и 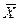 в уравнение массоотдачи, получим
в уравнение массоотдачи, получим
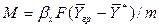 ,
,
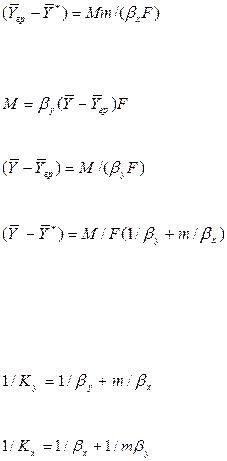
откуда
. |
(1.1) |
Из уравнения массоотдачи для газовой фазы
получим
. |
(1.2) |
Складывая выражения (1.1) и (1.2) и исключая неизвестную концентрацию на границе раздела фаз, получим
.
Из уравнения массопередачи следует, что
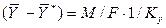 .
.
Приравнивая правые части и сокращая подобные члены, получим выражение для коэффициента массопередачи по газовой фазе
. |
(1.3) |
При выражении коэффициента массопередачи в концентрациях жидкой фазы получим
. |
(1.4) |
Левые части уравнений представляют собой общее сопротивление переносу вещества из фазы в фазу, т.е. сопротивление массопередаче, а правые части – сумму сопротивлений массоотдаче в фазах. Поэтому эти зависимости являются уравнениями аддитивности фазовых сопротивлений. Эти уравнения справедливы и для случая, если линия равновесия является кривой.
Вопрос №6. Материальный баланс и уравнение рабочей линии при абсорбции. Вывести это уравнение при противотоке. Как определяется минимальный удельный расход абсорбента?
В расчетах процесса абсорбции используются уравнения материального и энергетического балансов. В колонных абсорберах контакт фаз может осуществляться либо непрерывно, либо ступенчато, когда в каждой ступени фазы взаимодействуют друг с другом, а по выходу из ступени - разделяются. В обоих случаях эффективность массообмена определяется направлением относительного движения фаз и структурой их потоков. По направлению относительного движения фаз различают: противоток, прямоток и перекрестный ток.
Рассмотрим противоточную схему движения потоков в колонном аппарате для абсорбции (рис. 3.19), принятой в системах газоочистки. В аппарат поступают фазы G (газ) и L (жидкость). Пусть расход носителя в газовой фазе составляет G кг/с, а в жидкой фазе равен L кг/с. Содержание распределяемого компонента, выраженное в виде относительных весовых составов, в фазе G обозначим через Y, а в фазе L - через X.

Рис.3.19. Схема противоточного массообменного аппарата
При противотоке уравнения материального баланса для любого сечения колонны будут иметь вид:
После интегрирования этих уравнений для любого сечения колонны получим:
Эта зависимость является уравнением рабочей линии процесса массопередачи в противоточной колонне. Как видно из уравнения (3.9), при L/G = const рабочая линия в координатах х - у - прямая с тангенсом угла наклона к оси абсцисс, равным L/G.
На рис. 3.20 в координатах у – х показана рабочая линия АВ, а также линия равновесия ОС выражающая зависимость между равновесными концентрациями фаз. При абсорбции концентрация в газе выше равновесной и рабочая линия располагается выше линии равновесия.
Рис. 3.20. Взаимное расположение рабочей линии и линии равновесия.
Связь между составами материальных потоков и отношением их расходов при Gн ≈ Gк и Lн ≈ Lк можно представить зависимостью:
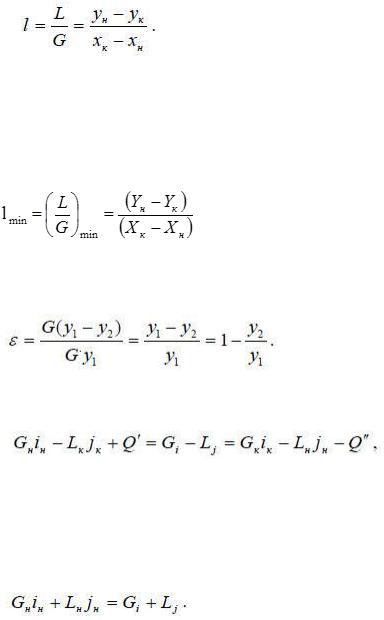
Величина l, определяемая из уравнения (3.10), является удельным расходом поглотителя (кг/кг инертного газа). При полном извлечении компонента из газа его содержание в газовой фазе не выходе из абсорбера было бы равно 0 (нулю), а количество поглощенного компонента составило бы G.у1. удельный расход абсорбента минимален (l=lmin), а движущая сила в точке касания равна нулю, поскольку в этой точке рабочая концентрация равна равновесной.
Значение lmin можно определить по уравнению:
Отношение количества фактически поглощенного компонента G(у1 - у2) к количеству, поглощаемому при полном извлечении, называется степенью извлечения:
Энергетический баланс для противотока:
где iн и jн - соответственно энтальпии потоков Gн и Lн; Q' - количество теплоты, вводимой в колонну на участке от места входа потока Gн до рассматриваемого сечения колонны; Q" - количество теплоты, подводимой на участке от рассматриваемого сечения колонны до выхода потока.
Если процесс проводится в адиабатических условиях, т. е. Q = 0, то
Чтобы построить рабочую линию, надо знать составы фаз на входе в абсорбер (у1, х2) и на выходе из него (у2, х1). По этим составам строят точки А и В, а расход поглотителя определяют по уравнению (3.10).
Однако обычно заданы только начальные составы газа и жидкости (у1, х2) и степень извлечения. Заданным условиям соответствует опреде-ленное значение у2 , которое можно найти по формуле (3.9) и таким образом построить точку В. В зависимости от удельного расхода поглотителя рабочая линия будет поворачиваться около точки В, причем точка А будет перемещаться по горизонтали, соответствующей ординате у1. Положение А*В, когда точка А* лежит на линии равновесия или когда рабочая линия касается линии равновесия, соответствует минимальному расходу поглотителя.
При минимальном расходе поглотителя движущая сила в точке касания рабочей линии и линии равновесия равна нулю, при этом требуется абсорбер бесконечно большой высоты. С увеличением удельного расхода поглотителя уменьшается требуемая высота абсорбера, но возрастают рас-ходы на десорбцию, на перекачивание поглотителя и т.д. Оптимальный удельный расход поглотителя можно найти технико-экономическим расчетом.
Вопрос №7. Вывести уравнение рабочей линии для массообменных аппаратов (на примере абсорберов) при противоточном движении фаз идеальным вытеснением в условиях неизменности их расхода.
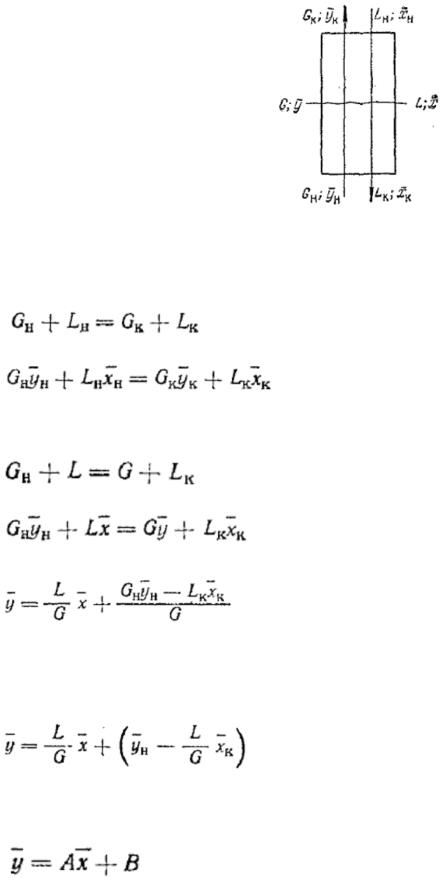
Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз. Пусть в процессе массопередачи из фазы в фазу, например, из газовой фазы в жидкую, переходит только один распределяемый компонент (скажем, аммиак).
Сверху в аппарат поступает Lн кг/сек жидкой фазы, содержащей |
н мас. долей распределяемого компонента, а снизу из |
|||
|
к |
|
|
|
аппарата удаляется Lк кг/сек той же фазы, содержащей ̅мас. долей распределяемого компонента. Снизу в аппарат |
||||
|
|
н |
|
|
поступает Gн кг/сек другой фазы (газовой) концентрацией ̅ |
и сверху удаляется Gк кг/сек этой фазы, имеющей |
|||
к |
|
|
|
|
концентрацию ̅ |
мас. долей распределяемого компонента. |
|
|
|
Тогда материальный баланс по всему веществу:
Материальный баланс по распределяемому компоненту:
Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до̅некоторого̅ произвольного сечения, для которого расходы фаз составляют G и L кг/сек, а их текущие концентрации равны и соответственно.
По всему веществу:
По распределяемому компоненту:
Решая это уравнение относительно , получим:
(*)
Уравнение (*) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.
Если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с=достаточной= для практических целей точностью считать постоянными, т.е. принять L=const и G=const. При этом к , н и уравнение
(*) приводится к виду:
Вводя обозначения 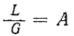 и
и 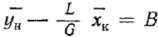 , находим уравнение рабочей линии, которым обычно пользуются при расчете для массообменных процессов:
, находим уравнение рабочей линии, которым обычно пользуются при расчете для массообменных процессов:
Вопрос №8. Вывод уравнения для расчета средней движущей силы массопередачи.
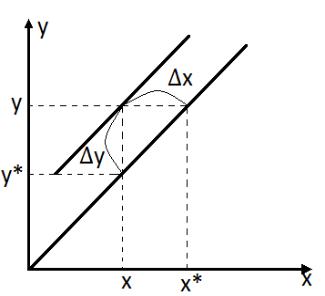
Разность между рабочими и равновесными концентрациями называется движущей силой массообменных процессов. ∆Тогда= для−жидкой и газовой фаз получим:
∆ = − – для жидкой фазы
, –для газовой фазы
Где - равновесные концентрации, x, y – рабочие концентрации.
Таким образом, движущая сила характеризует степень отклонения системы от равновесия. При установлении равновесия между фазами массообмен между ними прекращается. Как и при теплообмене, величина движущей силы массообменных процессов зависит от относительного направления движения фаз (противоток, прямоток и др.). Также на движущую силу большое влияние оказывает гидродинамическая структура потоков.
Для потока абсорбтива через А можем записать (в |
||||
∆̇ = |
|
( − ) |
(1) |
|
соответствии с основным уравнением массопередачи): |
||||
|
|
∫0 |
|
|
∆ ̇ = |
|
( − ) |
(2) |
|
|
|
∫0 |
|
|
|
|
|
|
|
Где |
, – коэффициенты массопередачи; А – площадь |
|||
поверхности контакта фаз; dA – площадь элемента поверхности.
Концентрации фаз изменяются при их движении вдоль поверхности раздела (контакта), соответственно, изменяется движущая сила массопередачи. Поэтому в
уравнение массопередачи вводят величину средней |
|||
ср |
|
ср |
|
движущей силы (∆ |
или ∆ |
|
). |
∆̇ = |
|
∙ ∙ ∆ |
(3) |
||
Тогда можем записать: |
|||||
|
|
|
ср |
|
|
∆ ̇ = |
|
∙ ∙ ∆ |
(4) |
||
|
|
|
ср |
|
|
∆ ср = |
А1 |
∫0А( |
− ) (5) |
||
Приравняв выражения (1) и (3) и (2) и (4), получим: |
|||||
∆ = |
1 |
|
( − ) (6) |
||
ср |
А |
∫0 |
|
|
|
Выражения (5) и (6) соответствуют среднеинтегральным движущим силам по поверхности массопередачи. |
|||||
|
|
|
1. |
̇ = |
|
Допущения, принимаемые для вывода уравнения средней движущей силы массопередачи |
|||||
|
|
|
|
|
|
|
|
|
2. |
̇ = |
|
|
|
|
|
|
|
|
|
|
3. |
, = |
|
|
|
|
|
|
|
|
|
|
4. |
Модель идеального вытеснения |
|
|
|
|
5. |
Противоток фаз |
|
В результате массопередачи на элементе поверхности dA концентрация фазы y уменьшается на величину dy, тогда для |
|||||||||||
межфазного потока абсорбтива через dA: |
|||||||||||
̇ = ̇(−) |
(7) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
̇ = |
( − ) |
|
(8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Минус в уравнении (7) указывает на уменьшение концентрации. Приравняем уравнения (7) и (8) |
|||||||||||
−̇ = |
|
( − ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Разделим переменные |
|
|
|||||||||
|
|
|
|
|
∙ |
|
|
|
|||
− − = |
|
|
|
|
|
|
|
|
|||
|
|
̇ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Укажем пределы интегрирования |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
к |
|
|
|
|
|
|
|
|||
− ∫ |
|
|
|
|
|
= ∫ |
|
|
|||
|
− |
|
̇ |
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
Проинтегрируем правую часть уравнения
∫ к |
|
= |
∙ |
(9) |
||||
|
− |
|
|
|
̇ |
|
||
н |
|
|
|
|
|
|
|
|
̇ = |
∙ |
|
|
(10) |
||||
|
|
|
|
|
|
|
|
|
Выразим мольный расход инерта из уравнения (9) |
||||||||
|
|
|
|
|
|
|
||
|
|
∫ нк |
|
|
|
|||
|
|
− |
|
|||||
Мольный расход межфазного потока абсорбтива также можно |
|||||||||
∆ ̇ = ̇( − ) |
(11) |
||||||||
выразить через мольный расход инерта. Получим: |
|||||||||
|
|
|
н |
к |
|
|
|
||
Подставим мольный расход инерта из уравнения (10) в |
|||||||||
∆ ̇ = |
∙ |
н− к |
∙ |
(12) |
|||||
уравнение (11) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
∫ кн |
|
|
|
|
|
|
∆ = |
|
|
− |
|
|
|
|||
н− к |
(14) |
|
|
||||||
Сравним полученное выражение с уравнением (4).Получим: |
|||||||||
ср |
|
|
|
|
|
|
|
||
|
∫ кн |
|
|
|
|
|
|
||
|
− |
|
|
|
|
||||
Уравнение 14 выражает среднюю движущую силу процесса
|
|
|
|
|
|
|
|
|
массопередачи. Аналогично оно выглядит и для жидкой фазы. |
||||||||
|
|
|
|
|
|
|
|
|
= ∫ |
н |
|
|
|
|
|
|
|
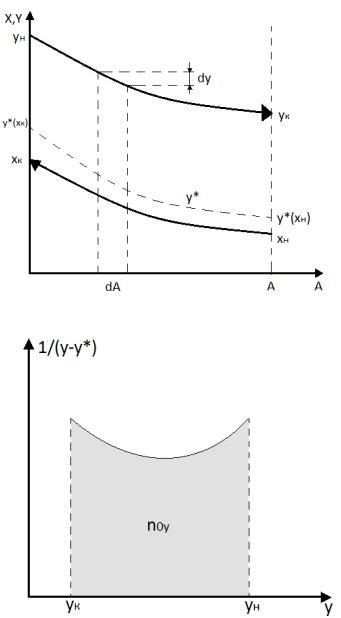
Также его можно выразить через число единиц переноса n0y: |
||||||||
0 |
|
|
− |
|
|
|
||
∆ = |
н− к ; |
∆ = к− н |
||||||
|
к |
|
|
|
|
|
|
|
ср |
|
|
|
|
|
ср |
|
|
|
0 |
|
|
|||||
|
|
|
|
0 |
||||
Частный случай уравнения движущей силы массопередачи.
Рабочая линия – прямая вида y = ax + b. Равновесная линия – |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
прямая вида y* = ɱx, где ɱ - константа фазового равновесия. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
= |
− |
|
; |
|
|
= ɱ ∙ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Преобразуем y = f(x) в x = f(y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
∫ н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= [∫ ∙ + |
= ( ∙ + |
|
|
|
|
|
||||||||||||
− |
|
= |
∫ |
н |
|
|
− |
= ∫ н |
|
|
|
|
ɱ ɱ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
к |
|
= |
|
|
|
|
|
|
|
к |
|
−ɱ∙ |
|
|
|
|
|
|
|
|
к |
|
|
(1− )∙+ ∙ |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||||||
)] |
|
|
|
|
ɱ |
[(1 − |
|
|
|
) ∙ + |
|
|
|
∙ ] |
| |
|
= |
|
|
|
|
|
ɱ |
|
ɱ |
ɱ |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ɱ |
|
|
|
|
|
|
|
|
ɱ |
|
|
|
|
н |
|
|
|
|
|
|
1 |
|
|
|
(1− |
ɱ)∙ н+ɱ∙ |
|
|
|
|
|
|
|
||||||||
|
|
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
1− |
|
|
(1− |
)∙к+ |
∙ |
|
|
|
|
|
|
|
|||||||||
1− ɱ − |
ɱ( − ) = |
|
|
1− ɱ |
− ɱ∙ |
|
(15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
н− |
ɱ |
( н− ) |
|
|
|
|
|
1 |
|
|
|
|
н−ɱ∙ к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
к |
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Но = ɱ ∙ |
, поэтому |
|
= ɱ ∙ |
к |
и |
|
= ɱ ∙ . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
низа |
|
|
|
|
н |
|
|
|
|
|
к |
|
|
|
|
верха |
|
|
к |
|
|
|
н |
|
|
н |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Также ∆ |
|
|
|
= − |
|
ин∆ |
|
|
|
|
= |
−н |
|
. Тогда для уравнения |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∫ н |
|
|
|
= |
|
|
1ɱ н−ɱ∙к |
|
= |
|
|
|
1ɱ |
|
н |
|
|
к |
= |
|
1ɱ ∆низ (16) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
(15) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
− |
|
|
|
1− |
|
|
− ɱ∙ |
|
|
|
|
|
1− |
|
|
|
|
− |
|
|
|
|
1− |
|
∆ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
к |
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
верх |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∆ |
|
= |
|
|
|
|
н− к |
= |
|
|
|
|
|
|
ɱ |
|
|
|
|
|
|
|
|
|
|
н− |
ɱ |
н− к+ |
ɱ |
ɱ |
ɱ |
= |
ɱ |
|
|
ɱ |
( к− )] = ( н− ɱ∙ к)− ( к− ɱ∙ н) = ∆низ− ∆верх |
|||||||||||||||||||
|
|
|
|
|
|
|
(1− )(н− к) = |
|
|
к+ − |
|
[ н− |
( н− ) ]−[ к− |
|||||||||||||||||||||||||||||||||||||||||||
Подставим полученное выражение (16) в уравнение (14) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
ср |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
∆ |
низ |
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
∆ |
низ |
|
∆ |
∆ |
|||||
|
|
|
|
1− |
ɱ ∆ |
|
|
|
|
|
|
|
|
∆ низ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ низ |
|
|
|
|
|
∆ |
|
∆ низ |
∆ низ |
||||||||||||||||||
∆ |
|
= |
|
|
|
|
|
верх |
|
|
|
|
|
|
|
|
|
|
|
верх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
верх |
|
|
|
|
|
верх |
|
верх |
верх |
|||||||||
|
|
∆ низ− ∆ верх и ∆ |
|
|
|
|
= |
|
∆ низ− ∆ верх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
В итоге: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ср |
|
|
|
|
|
|
∆ |
низ |
|
|
|
|
|
|
|
ср |
|
|
|
|
|
|
|
∆ |
низ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
верх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
верх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вопрос №9 = №11
Вопрос №10. Расчет высоты и диаметра противоточных колонных аппаратов со ступенчатым контактом фаз.
|
4 |
|
|
|
|
|
|
|
|
|
|
Диаметр: = √ |
|
|
= |
|
> ; |
|
