2 сем / экз / пахт экз 2

PNud– по смыслу безразмерный коэффициент массоотдачи и PNud– величина искомая.

Поэтому: PNud = f2(Fod, Prd, Ho, Fr, Rr, Гi)=0

Для установившегося процесса PFod = 0,Ho = 0 PNud = f2(,Prd, Fr, Rr, Гi)=0 Критериальное уравнение процесса массотдачи обычно представляется в виде степенной зависимости:

Nud = A Fod 1 Prd 2 Hoa3 Fra4 Re 5 Гia6

Здесь PA, a1−6– экспериментально определённые коэффициенты.

Подобия гидромеханических, тепловых и массообменных процессов были рассмотрены для случая ламинарного движения среды с постоянными теплофизическими свойствами. Турбулентный режим не приводит к появлению новых критериев подобия. При турбулентном режиме меняется лишь вид зависимости между критериями.

8.Что называют «высотой единицы переноса массы»? Как используется это понятие при расчете массообменных аппаратов? Выведите уравнение аддитивности высот единиц переноса массы.

Высота единицы переноса (ВЕП) – величина, которая по смыслу выражает высоту массообменного аппарата, эквивалентную одной единице перенос Физический смысл ВЕП — высота участка рабочей части колонны, на котором достигается

изменение концентрации распределяемого компонента, равное средней на этом участке движущей силе процесса, подсчитанной с учетом отмеченных выше допущений.

Уравнение массоотдачи для всей поверхности: M = KyF∆yср. => F = M / (Ky∆yср)

Часто за основную характеристику массообменного аппарата принимают его высоту H. В этом случае трудно определимую величину F связывают с высотой аппарата следующим образом: F = Va = HSa, где S – поперечное сечение аппарата, S = Q/W; a – удельная поверхность контакта фаз, м2/м3.

Откуда H = F/(Sa).

Тогда по смыслу n0y и n0x – общее число единиц переноса (ЧЕП) — изменение рабочей концентрации распределяемого между фазами вещества, приходящееся на единицу движущей силы.

G G

Обозначим KySa = hoy и KxSa = hox

h0y и h0x – выражают высоту массообменного аппарата, эквивалентную одной единице переноса, или высоту единицы переноса (ВЕП).

аддитивности для ВЕП.

L

Аналогично, !hox = hx + mG hy

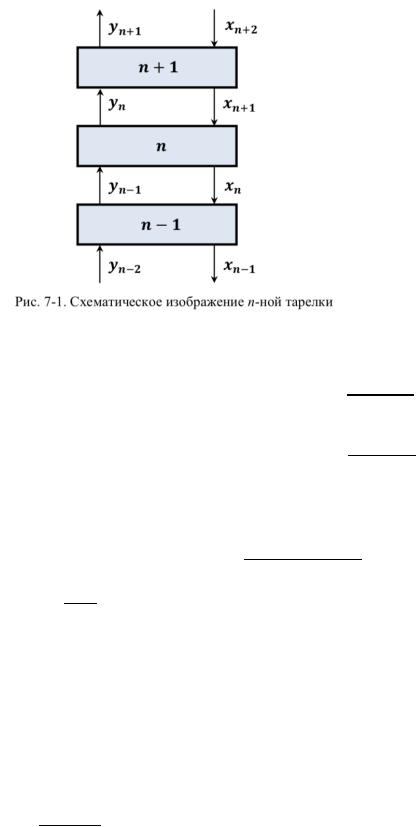
9.Что называют «эффективностью (кпд) тарелки по Мерфри»? Выведите зависимость между эффективностью по Мёрфри и числом единиц переноса массы на одну тарелку при идеальном смешении жидкости и идеальном вытеснении газа (пара).

Эффективность ступени (тарелки) по Мерфри (КПД Мерфри) выражают отношением изменения концентрации данной фазы на ступени к движущей силе на входе той же фазы в

P ступень.

Рассмотрим КПД Мерфри для n-ной ступени ректификационной колонны (рис. 7- 1):

Выраженные для разных фаз КПД Мерфри при линейной равновесной линии и

КПД Мерфри зависит от скорости массопереноса (т.е. от коэффициентов массоотдачи и числа единиц переноса), взаимного направления движения фаз, структуры потоков, площади поверхности контакта фаз и других факторов.

Связь числа единиц переноса и КПД Мерфри

Эффективность по Мэрфри очень просто связать с числами единиц переноса. Так, в случае режима идеального смешения в обеих фазах движущая сила на n-ной тарелке постоянна и равна:

P y = yx*n − yn (7-6)

Тогда пило единиц переноса:

Преобразуем уравнение (7-7), добавляя и вычитая Pn−1 :

Таким образом, в случае МИС в обеих фазах имеем:

Если принять режим идеального вытеснения в газовой фазе и режим идеального смешения в жидкой, то величина 1y* будет постоянной и равной Pyx*n ,

поскольку в пределах жидкой фазы концентрация будет постоянной и равной конечной Pn, тогда число единиц переноса:

Следует подчеркнуть, что выражения (7-9) и (7-13) основаны на идеализированных представлениях о структуре потоков на тарелках. Расчет числа реальных тарелок строится на основе более сложных моделей движения фаз, таких как ячеечная, ячеечная с обратными потоками, диффузионная. При этом их комбинируют, учитывая реальную картину движения фаз.

Модель идеального вытеснения для жидкой фазы при перекрёстном движении фаз:

PEy = Fm (eFmE0 − 1) (7-14)

где PE0 по уравнению (7-9), если газовая фаза соответствует модели идеального смешения, или по уравнению (7-13), если газовая фаза соответствует модели идеального вытеснения. Модель идеального вытеснения для обеих фаз при прямоточном движении:

1 − e−noy (1 + F1m )

PEy = 1 + F1m e−noy (1 + F1m ) (7-15)

Модель идеального вытеснения для обеих фаз при противоточном движении:

Ячеечная модель для жидкой фазы при перекрёстном движении фаз:

PEy = Fm [(s EF0 m + 1)s − 1] (7-17)

где PE0 по уравнению (7-9), если газовая фаза соответствует модели идеального смешения, или по уравнению (7-13), если газовая фаза соответствует модели идеального вытеснения, s- число ячеек идеального перемешивания (параметр ячеечной модели).

Диффузионная модель для жидкой фазы при перекрёстном движении фаз:

где PE0 по уравнению (7-9), если газовая фаза соответствует модели идеального смешения, или по уравнению (7-13), если газовая фаза соответствует модели идеального вытеснения, λ и η коэффициенты, рассчитываемые по уравнениям:

Pλ = η + Pex

где Pex – диффузионный критерий Пекле, характеризующий степень продольного перемешивания жидкости на тарелке:

l2

Pex = DL t

где Pl – длина пути жидкости на тарелке,PDL– коэффициент продольного перемешивания жидкости, P – среднее время пребывания жидкости на тарелке.

Величины PEy в выражениях (7-9) и (7-13) называют локальными эффективностями на тарелке, в отличие от эффективностей PEMy, рассчитываемых для переточных тарелок с

учетом взаимного направления движения фаз, неидеальности перемешивания, брызгоуноса, байпасирования жидкости и т.д.

10.Выведите уравнение рабочей линии укрепляющей части насадочной ректификационной колонны, указав соответствующие допущения. С какой целью получают это уравнение?

+

11.Выведите уравнение рабочей линии исчерпывающей части насадочной ректификационной колонны, указав соответствующие допущения. С какой целью получают это уравнение?

Ректификация - процесс разделения жидких смесей, который сводится к одновременно протекающей и многократно повторяемых процессов частичного испарения и конденсации разделяемый смеси на поверхности контакта фаз.

Рассмотрим непрерывную бинарную ректификацию (рис.3.13).

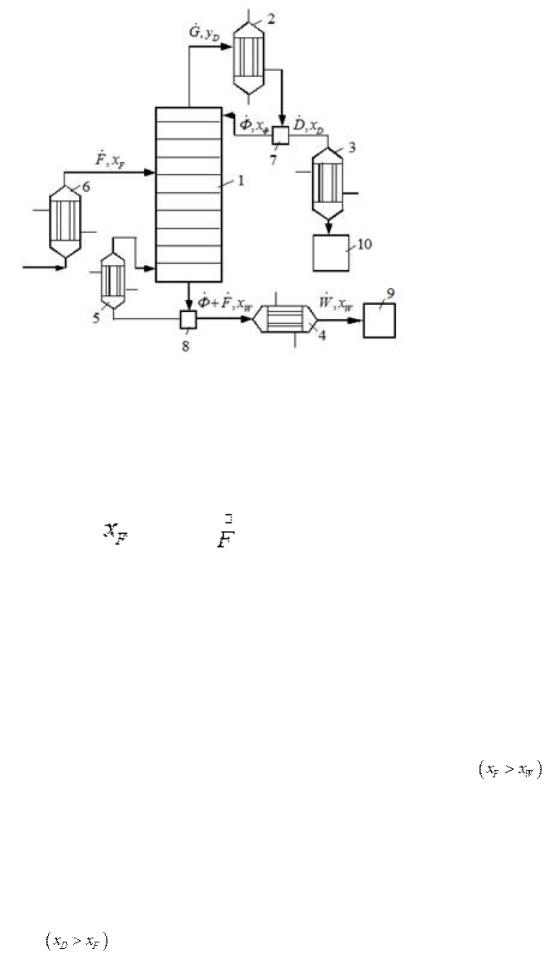
Рис. 3.13. Схема установки непрерывной ректификации: 1 - ректификационная колонна; 2 - дефлегматор; 3 - холодильник дистиллята; 4 - холодильник кубового остатка; 5 - кипятильник кубового остатка; 6 - подогреватель исходной смеси; 7 - делитель флегмы; 8 - делитель кубового остатка; 9 - сборник кубового остатка; 10 - сборник дистиллята.

Рассмотрим работу ректификационной установки на примере тарельчатой колонны(принципиальных отличий в работе колонн других конструкций нет). Исходная

смесь состава B с расходом P поступает в подогреватель 6, где нагревается до температуры, как правило, близкой к температуре кипения и подается в колонну 1. Обычно исходная смесь подается в колонну в жидком состоянии, но иногда может подаваться в виде пара или смеси пара и жидкости. Тарелка, на которую поступает исходная смесь, называется

питательной или тарелкой питания.

Она делит колонну на две части: верхнюю, называемую укрепляющей, и нижнюю - исчерпывающую. Жидкость стекает с каждой тарелки на более нижнюю, контактируя с восходящим неравновесным потоком пара.

При этом из пара в жидкость переходит ВК, а из жидкости в пар - НК. Таким образом, жидкость, стекая вниз, обогащается ВК и из нижней части колонны отводится кубовый

остаток, в котором преобладает ВК по сравнению с исходной смесью P . Часть кубового остатка, разделяясь в делителе 8, отводится в виде конечного продукта в сборник 9, а другая - поступает в кипятильник 5, испаряется и подается в виде пара в колонну под нижнюю тарелку.

Пар проходит через тарелки, контактируя с жидкостью, обогащается НК и отводится из верхней части колонны в дефлегматор 2, где, как правило, полностью конденсируется. Конденсат разделяется в делителе 7 на две части, одна из которых отводится в виде дистиллята в сборник готового продукта 10. Содержание НК в нем выше, чем в исходной

смеси P . Другая часть конденсата, называемая флегмой, подается на верхнюю

тарелку и стекает вниз для обеспечения контакта с паром в верхней части колонны. Если в

дефлегматоре весь пар конденсируется то составы пара B , дистиллята B и флегмы B

одинаковы P и в делителе 7 происходит лишь разделение жидкого потока на части без изменения его состава.

При взаимодействии поднимающихся паров со стекающей жидкостью происходит частичная конденсация паров и частичное испарение жидкости (флегмы) за счет теплоты конденсации. При этом из пара конденсируется в основном ВК, а из флегмы, в основном, НК. Таким образом отекающая флегма непрерывно обогащаются ВК, а поднимающиеся пары – НК. Если вся жидкость, поступающая в кипятильник 5, испаряется, то состав пара, поступающего

в колонну B равен составу кубового остатка P .

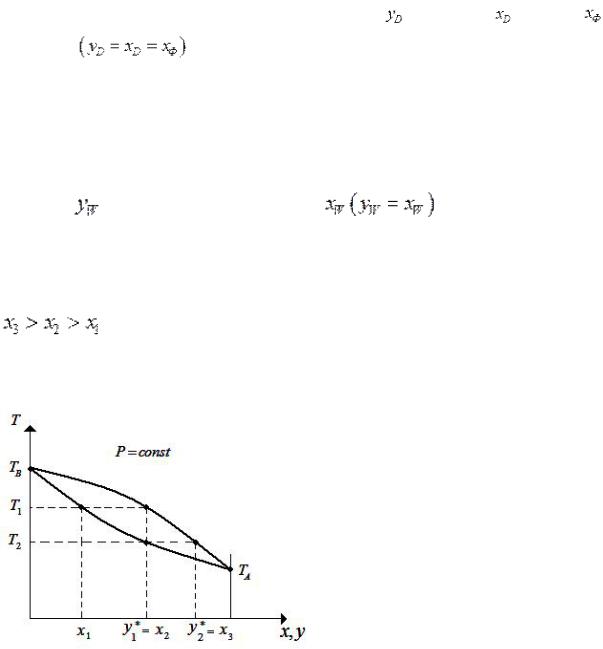
Исходная смесь состава x1 нагрета до Т1 кипения (рис.3.14). При этом получим пар, находящийся в равновесии с жидкостью. При конденсации этого пара образуется жидкость (конденсат) состава х2 =y1*, которая обогащена НК. Нагрев эту жидкость до Т2, и сконденсировав образующие пары, получим конденсат состава х3=y2*. Как видно

P .Таким образом можно получить жидкость, практически из НК.

Поскольку жидкость бинарная, кубовый остаток получил в виде почти чистого ВК.

Рис.3.14. Фазовая диаграмма Т – x,y при Р=const.

Процесс ректификации осуществляется периодически или непрерывно, при ратм, рвак и ризб. Для непрерывного процесса ректификации необходимо, чтобы исходная смесь соприкасалась со встречным потоком пара с несколько большей концентрацией ВК, чем в жидкой смеси. Положение питающей тарелки рассчитывают с учетом этого обстоятельства.

Для удобства анализа и расчета процесса ректификации вводят понятие о флегмовом числе R. Отношение киломолей флегмы Ф, приходящейся на 1 кмоль отбираемого дистиллята D, называют флегмовым числом:

R=Ф/D (3.16)

3.4.1. Материальный баланс непрерывной ректификации бинарных смесей.

Известно два основных метода анализа работы и расчета ректификационных колонн: графоаналитический (проще графический) и аналитический. Рассмотрим более простой и наглядный графический метод.

Введем основные допущения:

-молярные теплоты испарения или конденсации компонентов при одной и той же температуре приблизительно одинаковы. Отсюда следует, что при конденсации 1кмоль ВК в колонне испаряется 1кмоль НК, т.е. количество паров (в кмолях), поднимающихся по колонне постоянно;

-дефлегматоре не происходит изменение состава пара. Если пар полностью конденсируется в

-при испарении жидкости в кипятильнике не происходит изменения ее состава. Следовательно, состав пара, образующегося в кипятильнике, соответствует составу кубового остатка: yW=xW;

-теплоты смешения компонентов разделяемой смеси равны нулю.

Кроме того, смесь, подлежащая разделению, поступает в колонну нагретая до температуры кипения на питающей тарелке. Эти допущения мало искажают реальный процесс, но существенно упрощают расчет.

Материальный баланс колонны по всему потоку:

Уравнения рабочих линий.

Поскольку условия работы укрепляющей и исчерпывающей частей ректификационной колоны различны, поэтому материальный баланс для них рассмотрим отдельно (рис.3.15).

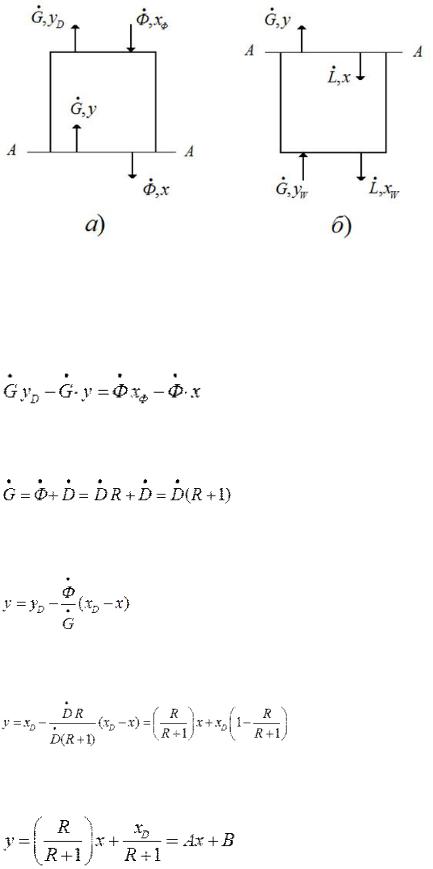
Рис. 3.15. Схема материального баланса ректификационной колонны: а – укрепляющая часть, б – исчерпывающая часть.

Укрепляющая часть. Верх Составим материальный баланс по НК для верха этой части колонны:

Количество поднимающихся паров по колонне:

P

По (3.20) находим y:

По условию yD=xD, и меняя получим:

Окончательно:

Это и есть уравнение рабочей линии укрепляющей части колонны, которая является уравнением прямой линии. Это уравнение справедливо до сечения ввода исходной смеси, т.е. до точки b, соответствующий концентрации xF.

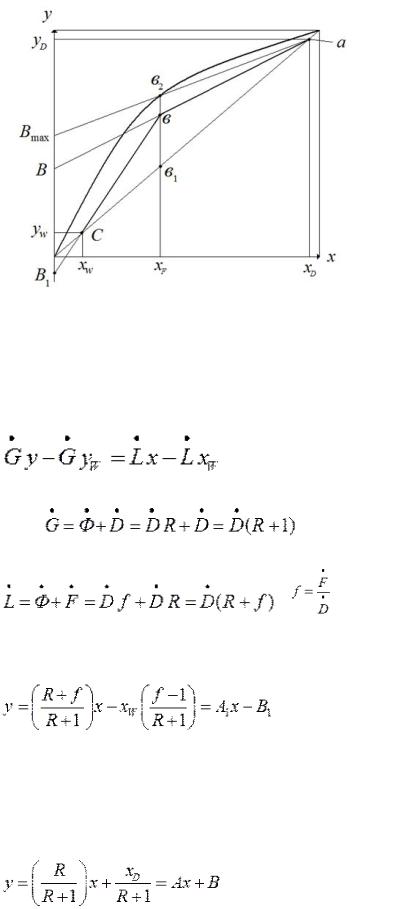
Рис.3.16. Рабочие линии и линия равновесия ректификационной колонны.

Исчерпывающая часть. Низ Рассмотрим материальный баланс для низа исчерпывающей части колонны - ниже произвольного сечения В-В, где текущие концентрации НК в фазах x и y (рис. 5.38):

При х=хW, у=уW=xW, т.е. рабочая линия исчерпывающей части колонны проходит через точку, лежащей на диагонали с абсциссой хW.

ИТОГО

Положение точек P и c определены, они лежат на диагонали. Точка в пересечении линий

и сВ1. Положение точки b соответствует xF, т.е. соответствует сечению, на уровне которого подают питание в колонну.

Для определения числа теоретических ступеней изменения концентрации между рабочей и

https://megapredmet.ru/1-63674.html

Вопросы 2

1.Напишите основные уравнения массопередачи и уравнения массоотдачи. Что фактически является и что принято считать движущей силой того или иного процесса? Каков физический смысл коэффициентов массопередачи и массоотдачи и каково соотношение между ними (без вывода)?

Основное уравнение массопередачи

В массообменных процессах вещество путем диффузии переходит из одной фазы в другую, причем компонент, который переходит называется распределяемым веществом.

Основной характеристикой массообменных процессов является скорость массопередачи, которая представляет собой количество распределяемого вещества PM (кг), переходящего из одной фазы в другую через единицу поверхности соприкосновения фаз PF (м ²) в единицу

времени τ , т.е. PM (кг/м2 с)

F τ

Скорость процесса массопередачи пропорциональна его движущей силе, которая равна разности концентраций P y = y − y* , где у– концентрация распределяемого вещества в первой фазе, откуда вещество уходит; у* - концентрация распределяемого вещества у поверхности раздела фаз (со стороны первой

фазы), при которой бы существовало равновесие с концентрацией второй фазы х.

1

PR = Ky- коэффициент массопередачи. Т.к. концентрации фаз в ходе процесса меняются, то

изменяется и P y . Поэтому вводится понятие средней движущей силы 8 ycp.

PM = KyF ycpτ - основное уравнение массопередачи, где М-нагрузка аппарата. В условиях

Коэффициент массопередачи– это количество вещества, переданного из одной фазы в другую через единицу поверхности в единицу времени при движущей силе равной единице. Движущая сила одного и того массообменного процесса может быть выражена разностью концентраций и по другой фазе: