
билеты 19
.pdf
газовую фазу переходят электроны, создавая электронное облако со стороны газовой фазы.
2.Образование двойного электрического слоя происходит в результате адсорбции. Двойной электрический слой может образоваться при избирательной адсорбции в межфазном слое ионов электролитов, не входящих в состав веществ, образующих фазы, т. е. в результате адсорбции примесей.
3.Если вещества, составляющие фазы системы, не способны обмениваться зарядами, то двойной электрический слой может образоваться благодаря ориентированию полярных молекул сопряженных фаз в результате их взаимодействия.
Из объединенных первого и второго начал термодинамики, а также полного дифференциала энергии Гиббса выводится первое уравнение Липпмана, связывающее электрический потенциал с поверхностным натяжением:
J
Если знаки потенциала и заряда совпадают, то поверхностное натяжение снижается с ростом потенциала. Если же их знаки противоположны, то увеличение потенциала ведет к росту поверхностного натяжения. Эти зависимости тем сильнее,чем больше абсолютное значение плотности заряда. При минимальной плотности заряда поверхностное натяжение слабо зависит от потенциала.
Дифференциальная емкость двойного электрического слоя, как н любого конденсатора, определяется соотношением:
J
После дифференцирования первого уравнения Липмана по φ и подстановки в него данного соотношения получим второе уравнение Липпмана:
J
Это уравнение показывает возможность определения емкости двойного электрического слоя, если известна зависимость σ от φ.
J
Это уравнение называют уравнением электрокапиллярной кривой. Из него следует, что поверхностное натяжение при условии постоянства емкости двойного электрического слоя изменяется в соответствии с уравнением параболы.
J
Вершина параболы отвечает максимальному поверхностному натяжению σмакс. Парабола симметрична, что по физическому смыслу означает равное сродство катионов и анионов, выступающих в роли противоионов, к поверхности, имеющей соответственно отрицательный

и положительный потенциал. Уменьшение положительного потенциала, как и отрицательного, ведет к увеличению поверхностного натяжения. Однако в реальных системах емкость двойного электрического слоя несколько изменяется с изменением потенциала, и поэтому экспериментальные электрокапиллярные кривые обычно не являются симметричными.
Вершина параболы соответствует точке нулевого заряда. В этой точке поверхностное натяжение не зависит от потенциала, так как производная dσ/dφ равна нулю, т. е. поверхностный слой имеет нулевой заряд, что означает отсутствие двойного электрического слоя. Потенциал же поверхности в этой, точке не равен нулю.
3.Рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота, используя уравнение БЭТ. Площадь, занимаемая молекулой азота в плотном монослое, составляет 16·10-20 м2.
p/ps |
0,0286 |
0,136 |
0,200 |
|
|
|
|
A, моль/кг |
2,16 |
3,02 |
3,33 |
|
|
|
|
Билет 27
1.Предмет коллоидной химии. Признаки объектов коллоидной химии. Поверхностная энергия и поверхностные явления. Количественные характеристики дисперсности. Классификация дисперсных систем. Коллоидная химия и химическая технология.
Колло́идная хи́мия (др.-греч. κόλλα — клей) — наука о дисперсных системах и поверхностных явлениях, возникающих на границе раздела фаз. Изучает адгезию, адсорбцию, смачивание, коагуляцию, электро-поверхностные явления в дисперсных системах.
Признаки коллоидных систем:
1.Гетерогенность
2.Дисперсность.
Гетерогенность количественно определяется поверхностным натяжением — величиной, характеризующей энергию единицы поверхности и являющейся фактором интенсивности. Поверхностное натяжение определяет как бы степень гетерогенности, резкость перехода от одной фазы к другой, различие между соприкасающимися фазами. Чем сильнее выражена гетерогенность и чем более резко различаются по природе сопряженные фазы, тем больше поверхностное натяжение. Отсутствие гетерогенности равнозначно отсутствию поверхностного натяжения. Гетерогенным системам присуща поверхностная энергия: G = σ·s.
Второй признак — дисперсность. Дисперсность – величина, обратная поперечному размеру частиц: D=1/а. Системы с малой дисперсностью (менее 103 см-1) не принято рассматривать как коллоидные.
Широко применяется и третья характеристика раздробленности — удельная поверхность Sуд, определяемая отношением площади межфазной поверхности к объему тела s/V, Все три характеристики раздробленности связаны между собой: с уменьшением размера а увеличиваются дисперсность D и удельная поверхность Sуд.
Классификация по кинетическим свойствам:
1.Свободнодисперсные системы (частицы не связаны друг с другом, свободное броуновское движение)
2.Связнодисперсные системы (частицы образуют пространственную решетку) Классификация по размеру частиц:
1.Ультрамикрогетерогенные системы (золи): r = 1 – 100 нм
2.Микрогетерогенные системы (суспензии): r = 100 – 104 нм
3.Грубодисперсные системы: r = 0,1 – 10 мкм
Коллоидные явления широко распространены в химической технологии. Практически нет такого химического производства, которое бы не осуществлялось с участием поверхностных явлений и дисперсных систем. Измельчение сырья и промежуточных продуктов, обогащение, в том числе флотация, сгущение, отстаивание и фильтрация, конденсация, кристаллизация и вообще процессы образования новых фаз, брикетирование, спекание, гранулирование — все эти процессы протекают в дисперсных системах, и в них большую роль играют такие коллоидно-химические явления, как смачивание, капиллярность, адсорбция, седиментация, коагуляция.
Большое распространение в химической технологии получили адсорбенты и катализаторы, которые представляют собой дисперсные системы с твердой дисперсионной средой. Адсорбция имеет самостоятельное значение для очистки и разделения веществ, извлечения ценных компонентов, хроматографии и др.
Как правило, все гетерогенные процессы в химической технологии для увеличения их скорости проводят при максимальной поверхности контакта фаз. Это значит, что системы в реакционных аппаратах находятся в состоянии суспензий, паст, пульп, эмульсий, пен, порошков, туманов, пылей. Несмотря на то что толщина поверхностных слоев не превышает несколько молекул, их роль не менее важна, чем объемных фаз, например, в процессах массопередачи (адсорбция, экстракция, сушка, испарение и др.), термоэлектронной эмиссии, смазочном действии, адгезии.
2.Общие представления о теории строения ДЭС. Уравнение Пуассона-Больцмана для диффузной части ДЭС и его решение для случая слабозаряженных поверхностей. Уравнение Гуи-Чемпена.
Двойной электрический слой состоит из ионов одного знака, прочно связанных с дисперсной твердой фазой, и эквивалентного количества противоположно заряженных ионов, находящихся в жидкой дисперсной среде вблизи межфазной поверхности.
Дисперсионная среда представляется как непрерывная фаза, влияние которой на двойной электрический слой определяется лишь ее диэлектрической проницаемостью. Существует несколько теорий описания двойного электрического слоя.
Теория Гельмгольца. Двойной электрический слой представляется как бы плоским конденсатором, одна обкладка которого может быть связана с поверхностью твердого тела, а другая обкладка, несущая противоположный заряд, находится на очень малом расстоянии от первой.
Недостатком этой теории является то, что толщина двойного электрического слоя очень мала и приближается к молекулярным размерам. Скачок электрокинетического потенциала, по теории Гельмгольца является разной величиной по сравнению с обычным электрохимическим потенциалом, и поэтому это теорию отвергли, и она представляет только исторический интерес.
Теория Гуи. По этой теории противоионы в двойном электрическом слое не могут быть сосредоточены у поверхности и образовывать монослой, они рассеяны в жидкой фазе на расстоянии от границы раздела. Такая теория структуры двойного электрического слоя определяется электрическим полем у твердой фазы и тепловым движением ионов, вследствие чего противоионы стремятся рассеяться во всем объеме жидкой фазы.
Эта теория не объясняет различного действия разных по природе противоионов одинаковой валентности на двойной электрический слой. Согласно ей введение одинакового количества противоионов одинаковой валентности сжимает слой и вызывает падение потенциала. Тогда исходя из таких соображений теория применима к достаточно разбавленным растворам коллоидов.
Теория Штерна. О. Штерн, разрабатывая свою теорию, исходил из двух предпосылок: он принял, что ионы имеют конечные, вполне определенные размеры, учел специфическое, неэлектрическое взаимодействие ионов с твердой фазой. По теории Штерна, первый слой противоионов притягивается к стенке под влиянием электростатических и адсорбционных сил. В результате чего часть противоионов удерживается поверхностью на очень близком расстоянии.
При введении электролита в систему слой будет сжиматься, все большее и большее число будет попадать в адсорбционный слой. При уменьшении концентрации увеличивается толщина слоя, т. к. при разбавлении системы потенциал должен возрастать, вместе с этим может наблюдаться десорбция, что приведет также к падению потенциала. При изменении температуры (повышении) потенциал должен расти вследствие возрастания интенсивности теплового движения противоионов и увеличения двойного электрического слоя, в случае понижения температуры наблюдается процесс, обратный первому.
pH-среда влияет на число положительных и отрицательных зарядов на поверхности. Природа дисперсионных сил влияет так: потенциал дисперсной фазы тем больше, чем больше полярность растворителя, поэтому наличие двойного электрического слоя на межфазной границе характерно для систем с полярными дисперсионными средами.
Чем больше полярность жидкости, характеризуемая ее диэлектрической проницаемостью и дипольным моментом молекулы, тем выше скорость электроосмотического переноса частиц. На двойной электрический слой влияют электроповерхностные силы, носящие неравновесный характер.
Деформация слоя может идти при действии гравитационного поля, механических вибраций, броуновского движения, конвективных потоков жидкой среды.
бщие представления о теориях строения ДЭС. Уравнение Пуассона-Больцмана для диффузной части ДЭС

При контакте раствора электролита с твердой фазой возникает разность потенциалов: поверхность приобретает заряд, а в растворе у поверхности образуется слой, обогащенный ионами противоположного знака, – двойной электрический слой (ДЭС).
ДЭС впервые рассмотрен Г. Л. Ф. Гельмгольцем в виде плоского конденсатора с расстоянием между двумя рядами разноименно заряженных ионов, близким к диаметру молекул. Позднее бала предложена иная модель Гуи-Чепмена: ДЭС имеет диффузное строение, а концентрация противоионов (потенциалобразующих ионов) в поле действия поверхностного потенциала распределяется исходя из теплового движения. Современная теория строения ДЭС рассматривает слой в виде двух частей: одна находится у межфазной поверхности и образует адсорбционный слой (слой Гельмгольца) толщиной δ соответствующий диаметру находящихся в нем гидратированных ионов, другая – в диффузной части толщиной К, зависящей от свойств и состава раствора и коллоидной системы. Значение потенциала в слое Гельмгольца при удалении от потенциалобразующих ионов снижается линейно от ω0 до потенциала диффузного слоя, а затем изменяется по экспоненте. Толщина К соответствует
расстоянию, на котором потенциал диффузного слоя снижается в е раз (2,718 раза).
Концентрация ионов в диффузном слое на расстоянии х от границ раздела фаз пропорциональна распределению Больцмана:
где С – концентрация иона; i, z – валентности ионов в объеме раствора за пределами диффузного слоя; WX характеризует работу по перемещению 1 моля ионов из объема раствора на расстояние x до границы раздела фаз; F – число Фарадея; φх – потенциал на расстоянии х, изменяющийся от φх до φσ при х = σ.
Уравнение Пуассона — Больцмана:
J
Это уравнение после двойного интегрирования дает соотношение, выражающее закон изменения поверхностного потенциала от расстояния в диффузной части двойного электрического слоя и от свойств раствора. Чтобы в полной мере представлять возможности этого соотношения, лежащего в основе теории двойного электрического слоя, необходимо учитывать основные допущения и предположения, принятые Гуи и Чепменом при его выводе: двойной электрический слой является плоским, диэлектрическая проницаемость не зависит от расстояния х, ионы представляют собой точечные заряды (т. е. не имеют объема), при переводе противоионов из объема раствора в двойной электрический слой совершается работа только против электростатических сил.
Обычно уравнение Пуассона — Больцмана решают применительно к конкретным граничным условиям. Ниже приводится его решение при условии малости потенциала диффузного слоя
(φδ<<25 мВ).
Обозначим экспоненциальный показатель у фактора Больцмана через у. При малых значениях φ и соответственно y<<1 фактор Больцмана можно разложить в ряд Маклорена:
J
Если ограничиться двумя первыми членами ряда, то уравнение для объемной плотности заряда после этих преобразований примет вид:

J
Первый член правой части этого уравнения равен нулю. так как он включает сумму зарядов в объеме раствора, которая по условиям электронейтральности равна нулю, и поэтому окончательно имеем:
J
После такого преобразования уравнение Пуассона — Больцмана принимает следующую форму:
J
Выражение æ2 перед φх включает постоянные, характеризующие свойства раствора, поэтому можно считать, что они не изменяются с расстоянием от поверхности:
J
Окончательно имеем: 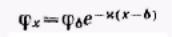
Если расстояние х отсчитывать от начала диффузной части двойного электрического слоя, то
Последние уравнения называются уравнениями Гуи-Чепмена, из них следует, что потенциал в области диффузного слоя в зависимости от расстояния уменьшается по экспоненте.
3.В таблице приведены данные по адсорбции паров воды макропористым адсорбентом при комнатой температуре. Пользуясь уравнением Ленгмюра определите емкость адсорбционного монослоя:
P·10-3, Па |
А, моль/кг |
|
|
4,68 |
6,28 |
|
|
7,72 |
9,22 |
|
|
17,77 |
14,89 |
|
|
P
