билеты 19

Для установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечениемS, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисуике отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество

дисперсной фазы за время τ переместится из объема 1 вправо: 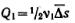,а из объема 2 влево

(в обратном направлении):.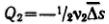

Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением

.

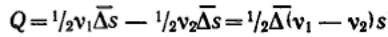Градиент концентрации по расстоянию в направлении диффузии можно выразить так:

Подставляя, получим: 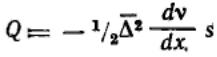Сравнивая это соотношение с первым законом диффузии Фика:

,окончательно имеем:

Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии н времени.

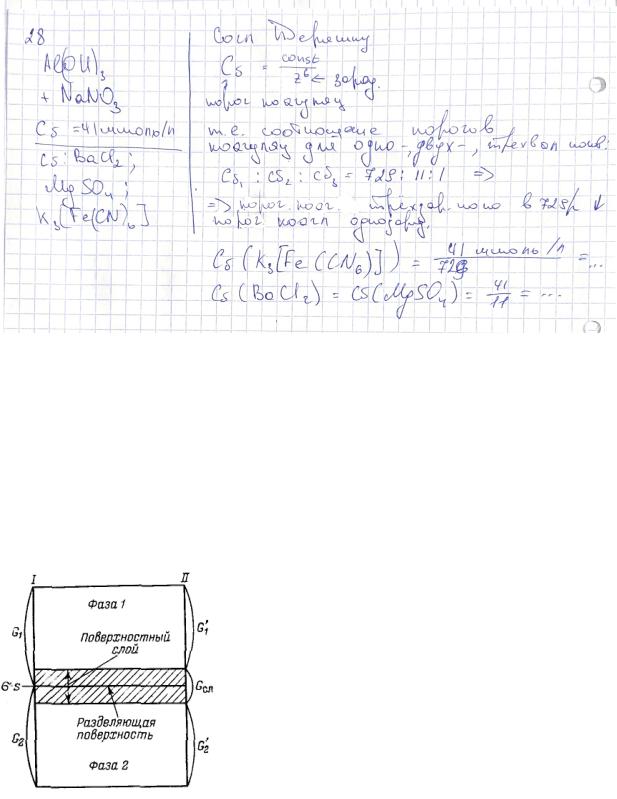
3.Для гидрозоля, содержащего положительно заряженные частицы гидроксиде

алюминия порог быстрой коагуляции при добавлении PNaNO3 равен 41 ммоль/л. Используя закон Дерягина, рассчитайте порог коагуляции для электролитов

PBaCl2, MgSO4, K3[Fe(CN )6

Билет 11

1.Метод избытков Гиббса. Вывод фундаментального адсорбционного уравнения Гиббса. Гиббсовская адсорбция. Частное выражение уравнения Гиббса. Поверхностная активность, поверхностно-активные и поверхностно-инактивные вещества.

Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины».

Чтобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса

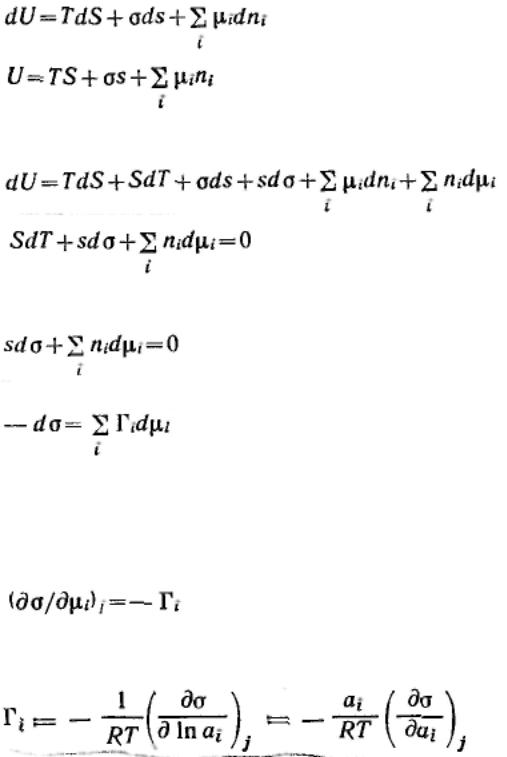
системы равна сумме энергий ГиббсаG1 и G2 объемных фаз 1, 2 и поверхностной энергии

Гиббса σs, которая является избыточной: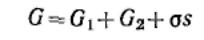

Характеристика величины адсорбции определяющася избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса). Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)

Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то и ее полный дифференциал от тех же переменных запишется следующим образом:

Подставляя значение dU, получим:

Для условия постоянства температуры это соотношение принимает вид

Разделив полученное уравнение на площадь поверхности, получим:

Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса. Для адсорбции одного конкретного вещества при постоянных химических потенциалах

других веществ полученное уравнение можно записать относительно частной производной для данного компонента:

Принимая во внимание, что 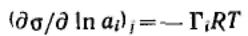Для гиббсовской адсорбции это выражение принимает вид

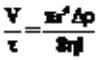
Общую зависимость напряжения сдвига от скорости деформации можно выразить в виде степенной функции: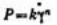

Если n = 1, то данное соотношение переходит в уравнение Ньютона.

Это двухпараметрическое уравнение известно под названием математической модели Оствальда — Вейля. Ньютоновская вязкость η неньютоновской стационарной жидкости

определяется уравнением .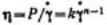

Если n = 1, жидкость является ньютоновской и константа k совпадает со значением ньютоновской вязкости (кривая 1). Таким образом, отклонение n от единицы характеризует степень отклонения свойств жидкости от ньютоновских.

Основы теории вязкости разбавленных лиозолей (суспензий) были заложены Эйнштейном. Он исходил из гидродинамических уравнений для систем макроскопических твердых сферических частиц,, которые при сдвиге приобретают дополнительное вращательное движение. Возникающее при этом рассеяние энергии является причиной возрастания вязкости. Эйнштейном была установлена связь между вязкостью дисперсной системы η и объемной долей дисперсной фазы φ: 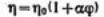Формула Эйнштейна не учитывает наличия у частиц поверхностных слоев, таких как

адсорбционные, сольватные и двойные электрические. Оно было получено в предположении отсутствия взаимодействия между частицами дисперсной фазы, поэтому оно справедливо только для разбавленных растворов. С увеличением концентрации дисперсной фазы взаимодействие частиц возрастает, и его необходимо учитывать.

Одним из приборов для определения вязкости является капиллярный вискозиметр. При измерении капиллярным вискозиметром, вязкость рассчитывают по уравнению Пуазейля:

J

Для исследования вязкости неньютоновских жидкостей используется ротационный вискозиметр.

3.Рассчитайте ζ-потенциал по данным электроосмоса через корундовую (Аl2О3) мембрану: при силе тока 0,015 A за 70 секунд перенесено 1,5 мл раствора, удельная электропроводимость которого χV = 0,013 См·м-1, поверхностная проводимость

χS = 0,006 См·м-1, η = 10-3 Па·с, ε = 81, ε0 = 8,85·10-12 Ф/м.

Билет 12

1.Поверхностное натяжение: термодинамическое определение, физический смысл, влияние природы взаимодействующих фаз. Вывод уравнения для полной (внутренней) энергии поверхностного слоя (уравнение ГиббсаГельмгольца). Зависимость термодинамических параметров поверхности от температуры.

Есть несколько определений поверхностного натяжения:

1.Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе

2.Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины.

3.Поверхностное натяжение – работа переноса молекул из объема тела на поверхность.

4.Термодинамическое определение поверхностного натяжения: Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:

J

При постоянных S, V, ni и q имеем:

J

т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде.

Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:

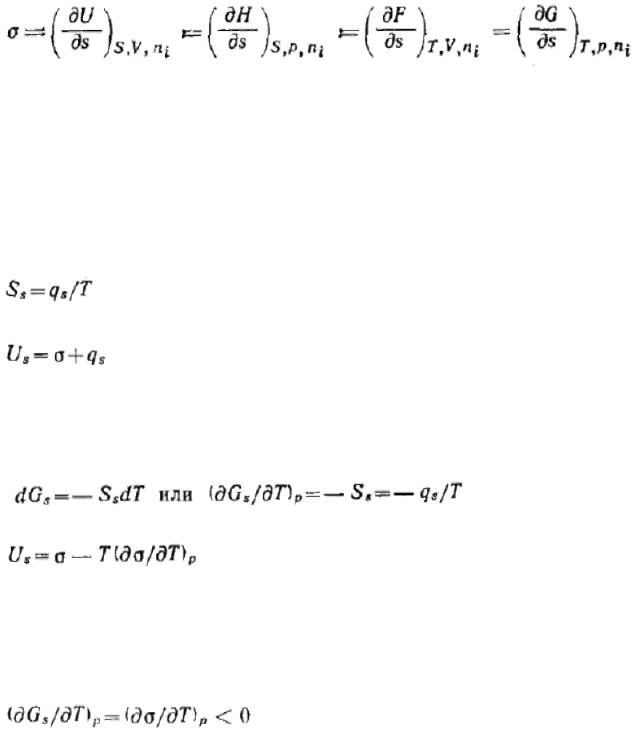
J

Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах.

Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади.

Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой.

В соответствии со вторым началом термодинамики избыточная энтропия равна

J

Учитывая, что Gs = σ, получим следующее выражение:

J

Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:

J

Подставлям это выражение в полученные уравнения:

J

Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:

J

Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.

2.Реологический метод исследования структур в дисперсных системах. Реологические модели идеальных тел (модели Гука, Ньютона, Сен-Венана-Кулона). Кривые течения реальных жидкообразных и твердообразных структурированных систем.

Структурно-механические свойства систем исследуют методами реологии — науки о деформациях и течении материальных систем. Реология изучает механические свойства систем по проявлению деформации под действием внешних напряжений. В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.

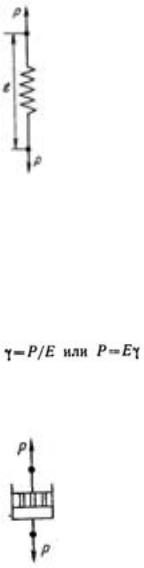
В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона.

Идеально упругое тело Гука представляют в виде спиральной пружины. В соответствии с законом Гука деформация а упругом теле пропорциональна напряжению сдвига P:

После снятия нагрузки идеально упругое тело Гука мгновенно переходит в первоначальное состояние (форму).

Идеально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью. Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости du/dx: 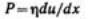Закон Ньютона можно сформулировать еще следующим образом: напряжение сдвига пропорционально скорости деформации (или скорость деформации пропорциональна

напряжению сдвига):

Моделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы. В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует,

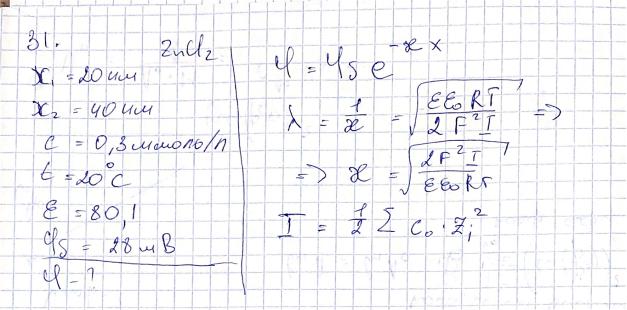
если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т.

е. при .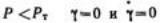

Если напряжение достигнет предела текучести, то развиваемая деформация идеально пластического тела не имеет предела, и течение происходит с любой скоростью, т. е. при

.

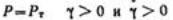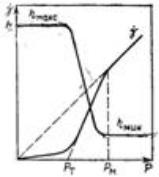
Кривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.

Из рисунка видно, что свойства структурированных жндкообразных систем могут быть охарактеризованы тремя величинами вязкости: двумя ньютоновскими ηмакс для неразрушенной структуры, ηмин Для предельно разрушенной структуры и пластической вязкостью η* в промежуточной области, моделируемой уравнением Бингама. Наличие структуры и ее прочность, особенно в жидкообразных системах, можно оценивать не только пределом текучести, но и разностью ηмакс — ηмин.

3.Используя уравнение Гуи-Чепмена, рассчитайте значение потенциала на расстоянии 20 и 40 нм от поверхности (пренебрегая толщиной слоя Гельмгольца). Дисперсионная среда водный раствор ZnCl2 с концентрацией 0,3 ммоль/л (индифферентный

электролит), t = 20 ºС, ε = 80,1; потенциал диффузного слоя 28 мВ

P

Билет 14

1.Особенности адсорбции на микропористых адсорбентах. Обобщенное уравнение теории Дубинина (теория объемного заполнения микропор), частные случаи этого уравнения (уравнение Дубинина-Радушкевича). Расчет общего объема микропор по изотерме адсорбции.

На первый взгляд может показаться, что закономерности заполнения микропор должны следовать теории капиллярной конденсации. Однако размеры микропор таковы, что в них происходит перекрытие полей поверхностных сил противоположных стенок пор, что значительно повышает энергию адсорбции и искажает профиль мениска конденсата в порах, соответствующий уравнению Кельвина, т. е. приводит к дополнительному всасыванию адсорбата, резкому увеличению адсорбционного потенциала.

Особенности адсорбции на микропористых телах проявляются в их избирательном действии. Избирательность, или селективность, микропористых адсорбентов существенно выше, чем

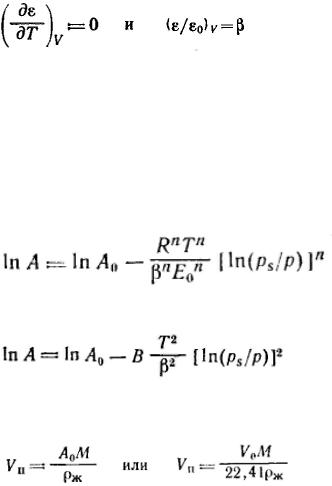
переходнопористых, благодаря тому, что большинство адсорбированных молекул взаимодействуют непосредственно с поверхностью адсорбента. В более крупных порах такое взаимодействие характерно только для первого слоя. В последующих же слоях взаимодействие не зависит от природы·, адсорбента, а определяется только природой адсорбата. Кроме этой особенности у микропор может проявляться так называемый ситовой эффект, заключающийся в том, что адсорбироваться могут только те молекулы, размеры которых меньше размеров микропор или равны им, в связи с чем все микропористые адсорбенты (не только цеолиты) называют молекулярными ситами.

Переходя к количественным соотношениям теории объемного заполнения пор, необходимо отметить, что в ее основе лежат представления потенциальной теории Поляни, предложенной первоначально для описания полимолекулярной адсорбции, исходя из двух основных параметров: адсорбционного потенциала ε, адсорбционного объема V и двух положений:

Степень заполнения адсорбента можно· представить как отношение величины адсорбции А к максимальной адсорбции А0, или как отношение заполненного объема V к предельному объему адсорбционного пространства V0, приведенных к нормальным условиям (давлению и температуре).

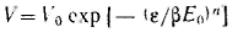или 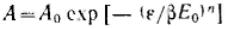Эти уравнения являются общими уравнениями теории объемного заполнения микропор.

Заменив адсорбционный потенциал на его выражение через давление пара (ε = RTln(p/ps)) и прологарифмировав общее уравнение теории объемного заполнения микропор, получим:

Для большинства активных углей n=2, тогда полученное уравнение переходит в уравнение Дубинина— Радушкевича:

Построение прямой в координатах 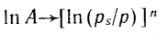дает возможности найти константы этого уравнения A0 и E. Объем микропор Vп рассчитывают по уравнениям

2.Факторы агреативной устойчивости лиофобных дисперсных систем. Электролитная коагуляция (концентрационная и нейтрализационная коагуляция). Правило ШульцеГарди и закон Дерягина. Способы стабилизаци лиофобных дисперсных систем.

Различают следующие термодинамические и кинетические факторы агрегативной устойчивости дисперсных систем:

1.Электростатический фактор заключается в уменьшении межфазного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана.

2.Адсорбционно-сольватный фактор состоит в уменьшении межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации)